Đề số 40 - Đề thi vào lớp 10 môn Toán
Đề thi vào lớp 10 môn Toán - Đề số 40 có đáp án và lời giải chi tiết
Đề bài
Bài 1 (2 điểm):
a) Tính giá trị biểu thức: \(A = 3\sqrt {27} - 2\sqrt {12} + 4\sqrt {48} .\)
b) Rút gọn biểu thức: \(B = \sqrt {7 - 4\sqrt 3 } + \dfrac{1}{{2 - \sqrt 3 }}.\)
Bài 2 (2,5 điểm): Giải các phương trình và hệ phương trình sau:
a) \({x^2} - 3x + 2 = 0\)
b) \({x^2} - 2\sqrt 3 x + 3 = 0\)
c) \({x^4} - 9{x^2} = 0\)
d) \(\left\{ \begin{array}{l}x - y = 3\\3x - 2y = 8\end{array} \right.\)
Bài 3 (1,5 điểm):
a) Trong mặt phẳng tọa độ Oxy, cho Parabol (P): \(y = {x^2}\) . Vẽ đồ thị Parabol (P).
b) Cho phương trình: \({x^2} - \left( {m - 1} \right)x - m = 0\,\,\,\left( 1 \right)\) ( với x là ẩn số, m là tham số). Xác định các giá trị của m để phương trình (1) có hai nghiệm phân biệt \({x_1};{x_2}\) thỏa mãn điều kiện: \({x_1}\left( {3 - {x_2}} \right) + 20 \ge 3\left( {3 - {x_2}} \right)\)
Bài 4 (3 điểm):
Quãng đường AB dài 160 km. Hai xe khởi hành cùng một lúc từ A để đi đến B. Vận tốc của xe thứ nhất lớn hơn vận tốc của xe thứ hai là 10 km/h nên xe thứ nhất đến B sớm hơn xe thứ hai là 48 phút. Tính vận tốc của xe thứ hai.
Bài 5 (1.0 điểm):
Cho tam giác ABC vuông tại A, đường cao AH. Gọi M là trung điểm của BC. Biết AB = 3 cm, AC = 4cm. Tính độ dài đường cao AH và diện tích tam giác ABM.
Bài 6 (2.5 điểm):
Cho tam giác nhọn ABC (AB < AC) nội tiếp đường tròn (O; R). Các đường cao AD, BE, CF của tam giác ABC cắt nhau tại H. Gọi M là trung điểm của BC.
a) Chứng minh tứ giác BFHD nội tiếp được đường tròn.
b) Biết \(\widehat {EBC} = {30^0}.\) Tính số đo \(\widehat {EMC}\) .
c) Chứng minh \(\widehat {FDE} = \widehat {FME}\)
Bài 7 (0,5 điểm): Cho \(a = \dfrac{{\sqrt 2 - 1}}{2};b = \dfrac{{\sqrt 2 + 1}}{2}.\) Tính \({a^7} + {b^7}\)
Lời giải chi tiết
Bài 1:
a) Tính giá trị biểu thức: \(A = 3\sqrt {27} - 2\sqrt {12} + 4\sqrt {48} .\)
\(\begin{array}{l}A = 3\sqrt {27} - 2\sqrt {12} + 4\sqrt {48} \\\;\;\; = 3\sqrt {{3^2}.3} - 2\sqrt {{2^2}.3} + 4.\sqrt {{4^2}.3} \\\;\;\; = 9\sqrt 3 - 4\sqrt 3 + 16\sqrt 3 \\\;\;\; = 21\sqrt 3 .\end{array}\)
Vậy \(A = 21\sqrt 3 .\)
b) Rút gọn biểu thức: \(B = \sqrt {7 - 4\sqrt 3 } + \dfrac{1}{{2 - \sqrt 3 }}.\)
\(\begin{array}{l}B = \sqrt {7 - 4\sqrt 3 } + \dfrac{1}{{2 - \sqrt 3 }} \\\;\;\;= \sqrt {{2^2} - 2.2\sqrt 3 + {{\left( {\sqrt 3 } \right)}^2}} + \dfrac{{2 + \sqrt 3 }}{{\left( {2 - \sqrt 3 } \right)\left( {2 + \sqrt 3 } \right)}}\\\;\;\; = \sqrt {{{\left( {2 - \sqrt 3 } \right)}^2}} + 2 + \sqrt 3 \\\;\;\;= 2 - \sqrt 3 + 2 + \sqrt 3 = 4.\\\;\;\;\left( {do\;\;2 - \sqrt 3 > 0} \right)\end{array}\)
Vậy B = 4.
Bài 2:
\(a)\;\;{x^2} - 3x + 2 = 0\)
Ta có: \(a + b + c = 1 - 3 + 2 = 0\) nên phương trình đã cho luôn có hai nghiệm phân biệt là: \({x_1} = 1;{x_2} = \dfrac{c}{a} = 2\)
Vậy tập nghiệm của phương trình là: \(S = \left\{ {1;2} \right\}\) .
\(\begin{array}{l}b)\;\;{x^2} - 2\sqrt 3 x + 3 = 0\\ \Leftrightarrow {\left( {x - \sqrt 3 } \right)^2} = 0\\ \Leftrightarrow x = \sqrt 3 .\end{array}\)
Vậy tập nghiệm của phương trình là: \(S = \left\{ {\sqrt 3 } \right\}\)
\(c)\;\;{x^4} - 9{x^2} = 0\\ \Leftrightarrow {x^2}\left( {{x^2} - 9} \right) = 0 \Leftrightarrow \left[ \begin{array}{l}x = 0\\x = - 3\\x = 3\end{array} \right..\)
Vậy tập nghiệm của phương trình là: \(S = \left\{ { - 3;0;3} \right\}\)
\(d)\;\;\left\{ \begin{array}{l}x - y = 3\\3x - 2y = 8\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}3x - 3y = 9\\3x - 2y = 8\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}y = - 1\\x = 3 + y\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}y = - 1\\x = 2\end{array} \right.\)
Vậy hệ phương trình đã cho có một nghiệm duy nhất: \(\left( {x;y} \right) = \left( {2; - 1} \right)\)
Bài 3:
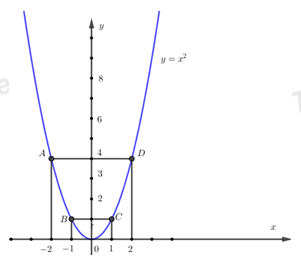
a) Trong mặt phẳng tọa độ Oxy, cho Parabol (P): \(y = {x^2}\) . Vẽ đồ thị Parabol (P).
Bảng giá trị
|
x |
\( - 2\) |
\( - 1\) |
0 |
1 |
2 |
|
y |
4 |
1 |
0 |
1 |
4 |
Khi đó đồ thị hàm số đã cho là 1 đường cong và đi qua các điểm \(A\left( { - 2;4} \right);B\left( { - 1;1} \right);C\left( {1;1} \right);D\left( {2;4} \right);O\left( {0;0} \right)\)
b) Cho phương trình: \({x^2} - \left( {m - 1} \right)x - m = 0\,\,\,\left( 1 \right)\) (với x là ẩn số, m là tham số). Xác định các giá trị của m để phương trình (1) có hai nghiệm phân biệt \({x_1};{x_2}\) thỏa mãn điều kiện: \({x_1}\left( {3 - {x_2}} \right) + 20 \ge 3\left( {3 - {x_2}} \right)\)
+) Phương trình có hai nghiệm phân biệt
\(\begin{array}{l} \Leftrightarrow \Delta > 0 \Leftrightarrow {\left( {m - 1} \right)^2} + 4m > 0\\ \Leftrightarrow {m^2} + 2m + 1 > 0\\ \Leftrightarrow {\left( {m + 1} \right)^2} > 0\\ \Leftrightarrow m \ne - 1\end{array}\)
+) Áp dụng hệ thức Vi-et cho phương trình (1) ta có: \(\left\{ \begin{array}{l}{x_1} + {x_2} = m - 1\\{x_1}.{x_2} = - m\end{array} \right.\)
Theo đầu bài ta có
\(\begin{array}{l}{x_1}\left( {3 - {x_2}} \right) + 20 \ge 3\left( {3 - {x_2}} \right)\\ \Leftrightarrow 3{x_1} - {x_1}{x_2} + 20 \ge 9 - 3{x_2}\\ \Leftrightarrow 3\left( {{x_1} + {x_2}} \right) - {x_1}{x_2} + 11 \ge 0\\ \Leftrightarrow 3.\left( {m - 1} \right) + m + 11 \ge 0\\ \Leftrightarrow 4m + 8 \ge 0\\ \Leftrightarrow m \ge - 2\end{array}\)
Kết hợp với điều kiện \(m \ne - 1\) ta có: \(m \ge - 2;m \ne - 1\) thỏa mãn yêu cầu bài toán.
Bài 4:
Quãng đường AB dài 160 km. Hai xe khởi hành cùng một lúc từ A để đi đến B. Vận tốc của xe thứ nhất lớn hơn vận tốc của xe thứ hai là 10 km/h nên xe thứ nhất đến B sớm hơn xe thứ hai là 48 phút. Tính vận tốc của xe thứ hai.
Gọi vận tốc của xe thứ hai là \(x\left( {km/h} \right),\,\,\left( {x > 0} \right)\)
Vận tốc của xe thứ nhất là: \(x + 10\left( {km/h} \right)\)
Thời gian xe thứ nhất đi hết quãng đường AB là:: \(\dfrac{{160}}{{x + 10}}\left( h \right)\)
Thời gian xe thứ hai đi hết quãng đường AB là: \(\dfrac{{160}}{x}\,\,\left( h \right)\)
Ta có xe thứ nhất đến B sớm hơn xe thứ hai là 48 phút: \( = \dfrac{{48}}{{60}} = \dfrac{4}{5}\,\,\left( h \right)\)
Theo bài ra ta có phương trình:
\(\begin{array}{l}\;\;\;\;\;\dfrac{{160}}{x} - \dfrac{{160}}{{x + 10}} = \dfrac{4}{5}\\ \Leftrightarrow 160.5.\left( {x + 10} \right) - 160.5.x = 4x\left( {x + 10} \right)\\ \Leftrightarrow 800x + 8000 - 800x = 4{x^2} + 40x\\ \Leftrightarrow {x^2} + 10x - 2000 = 0\\ \Leftrightarrow \left( {x - 40} \right)\left( {x + 50} \right) = 0\\ \Leftrightarrow \left[ \begin{array}{l}x - 40 = 0\\x + 50 = 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = 40\left( {tm} \right)\\x = - 50\left( {ktm} \right)\end{array} \right.\end{array}\)
Vậy xe thứ hai đi với vận tốc là: 40km/h.
Bài 5:
Áp dụng hệ thức lượng trong tam giác vuông ABC ta có:
\(\dfrac{1}{{A{H^2}}} = \dfrac{1}{{A{B^2}}} + \dfrac{1}{{A{C^2}}} = \dfrac{1}{{{3^2}}} + \dfrac{1}{{{4^2}}} = \dfrac{{25}}{{144}}\)
\(\Rightarrow AH = 2,4cm\)
Áp dụng định lý Pytago trong tam giác vuông ABC có
\(B{C^2} = A{B^2} + A{C^2} = {3^2} + {4^2} = 25\)
\(\Rightarrow BC = 5\left( {cm} \right)\)
Do M là trung điểm của BC nên ta có: \(BM = \dfrac{1}{2}BC = \dfrac{5}{2} = 2,5\left( {cm} \right)\)
Xét tam giác ABM có đường cao AH ta có: \({S_{ABM}} = \dfrac{1}{2}AH.BM = \dfrac{1}{2}.2,4.2,5 = 3\left( {c{m^2}} \right)\)
Bài 6:

a) Chứng minh tứ giác BFHD nội tiếp được đường tròn.
Ta có: AD, CF lần lượt là các đường cao của tam giác ABC nên: \(\widehat {ADB} = \widehat {BFC} = {90^0}\)\(\,\,\left( {hay\,\,\,\widehat {HDB} = \widehat {BFH} = {{90}^0}\,\,} \right)\)
Nên: \(\widehat {BFH} + \widehat {BDH} = {180^0}\)
Suy ra tứ giác BFHD nội tiếp được đường tròn đường kính BH với tâm là trung điểm của BH. (tổng 2 góc đối trong 1 tứ giác bằng \({180^0}\)
b) Biết \(\widehat {EBC} = {30^0}.\) Tính số đo \(\widehat {EMC}\) .
Ta có: \(\widehat {EBC} = {30^0}\) \( \Rightarrow \widehat {BCE} = {90^0} - {30^0} = {60^0}\,\,\left( {BE \bot EC\,} \right)\)
Xét tam giác vuông BEC vuông tại E có EM là trung tuyến nên: \(EM = MC = MB = \dfrac{1}{2}BC\)
Nên tam giác EMC là tam giác đều khi đó ta có: \(\widehat {EMC} = {60^0}\)
Vậy \(\widehat {EMC} = {60^0}\)
c) Chứng minh \(\widehat {FDE} = \widehat {FME}\)
Xét tứ giác BFEC ta có: \(\widehat {BFC} = \widehat {BEC} = {90^0}\left( {gt} \right)\)
Mà 2 đỉnh E, F kề nhau cùng nhìn cạnh BC dưới 1 góc vuông nên tứ giác BFEC nội tiếp.
\( \Rightarrow \widehat {EFC} = \widehat {EBC}\left( {\,hay\,\,\widehat {EFH} = \widehat {HBD}} \right)\) (2 góc nội tiếp cùng chắn cung EC) (1)
Mà tứ giác BFHD nội tiếp đường tròn (chứng minh câu a)
\( \Rightarrow \widehat {HBD} = \widehat {HFD}\) (2 góc nội tiếp cùng chắn cung HD) (2)
Từ (1) và (2) ta có: \(\widehat {EFH} = \widehat {HFD}\).
Mà \(\widehat {EFH} = \widehat {HAE}\) (tứ giác AFHE nội tiếp)
\(\widehat {HFD} = \widehat {HBD}\) (tứ giác BFHD nội tiếp)
Từ đó ta có:
\(\widehat {DFE} = \widehat {DFH} + \widehat {HFE} = 2\widehat {HAE} \)\(\,= 2\left( {{{90}^0} - \widehat {MEC}} \right) = {180^0} - 2\widehat {MEC} \)\(\,= \widehat {EMC}\) (do tam giác MEC cân tại M)
Xét tứ giác DFEM ta có: \(\widehat {DFE} = \widehat {EMC}\) nên tứ giác DFEM nội tiếp.
Vậy ta có: \(\widehat {FDE} = \widehat {FME}\)
Bài 7:
Ta có:
\(\begin{array}{l}a + b = \dfrac{{\sqrt 2 - 1}}{2} + \dfrac{{\sqrt 2 + 1}}{2} = \sqrt 2 \\a.b = \dfrac{{\sqrt 2 - 1}}{2}.\dfrac{{\sqrt 2 + 1}}{2} = \dfrac{1}{4}\end{array}\)
\({a^2} + {b^2} = {\left( {a + b} \right)^2} - 2ab = {\left( {\sqrt 2 } \right)^2} - 2.\dfrac{1}{4} = \dfrac{3}{2}\)
\({a^4} + {b^4} = {\left( {{a^2} + {b^2}} \right)^2} - 2{a^2}{b^2} \)\(\,= {\left( {\dfrac{3}{2}} \right)^2} - 2.{\left( {\dfrac{1}{4}} \right)^2} = \dfrac{{17}}{8}\)
\({a^3} + {b^3} = {\left( {a + b} \right)^3} - 3ab\left( {a + b} \right)\)\(\, = {\left( {\sqrt 2 } \right)^3} - 3\dfrac{1}{4}.\sqrt 2 = \dfrac{{5\sqrt 2 }}{4}\)
Do đó: \({a^7} + {b^7} = \left( {{a^3} + {b^3}} \right)\left( {{a^4} + {b^4}} \right) - {a^3}{b^3}\left( {a + b} \right) \)\(\,= \dfrac{{5\sqrt 2 }}{4}.\dfrac{{17}}{8} - {\left( {\dfrac{1}{4}} \right)^3}.\sqrt 2 = \dfrac{{169\sqrt 2 }}{{64}}\)