Đề thi giữa kì 1 Toán 6 - Đề số 15 — Không quảng cáo

Đề bài

Phần trắc nghiệm

Câu 1. Trong các cách viết sau đây, cách viết đúng là:

A. $1,5 \in {\rm{N}}$

B. $0 \in {{\rm{N}}^{\rm{*}}}$

C. $0 \in {\rm{N}}$

D. $0 \notin {\rm{N}}$

Câu 2. Cho tập hợp $H = \left\{ {x \in {N^{\rm{*}}}\mid x \le 10} \right\}$. Số phần tử của tập hợp H là:

A. 9 phần tử

B. 10 phần tử

C. 11 phần tử

D. 12 phần tử

Câu 3. Cho số 13 254 ta có:

A. Giá trị của chữ số 2 bằng nửa giá trị của chữ số 4

B. Giá trị của chữ số 2 bằng 5 lần giá trị của chữ số 4

C. Giá trị của chữ số 2 bằng 50 lần giá trị của chữ số 4

D. Giá trị của chữ số 2 bằng 500 lần giá trị của chữ số 4

Câu 4. Viết kết quả phép tính ${7^4}{.7^2}$ dưới dạng một lũy thừa ta được:

A. ${7^8}$

B. ${49^8}$

C. ${14^6}$

D. ${7^6}$

Câu 5. Viết kết quả phép tính ${4^6}:{4^3}$ dưới dạng một lũy thừa ta được:

A. ${1^3}$

B. ${4^3}$

C. ${4^2}$

D. 4

Câu 6 . Cho 4 số tự nhiên: 1234; 3456; 5675; 7890. Số vừa chia hết cho 2, vừa chia hết cho 5 là:

A. 1234

B. 3456

C. 5675

D. 7890

Câu 7 . Số các số nguyên tố nhỏ hơn 20 là:

A. 6 số

B. 7 số

C. 8 số

D. 9 số

Câu 8 . Trong các tổng dưới đây, tổng chia hết cho 7 là:

A. $14 + 35$

B. $21 + 15$

C. $17 + 49$

D. $70 + 27$

Câu 9 . ƯCLN(6,8) là:

A. 48

B. 36

C. 24

D. 2

Câu 10 . Trong các hình sau đây, hình nào là hình lục giác đều?

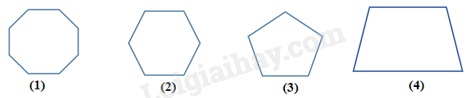
A. Hình (1)

B. Hình (2)

C. Hình (3)

D. Hình (4)

Câu 1 1 . Hai đường chéo của hình chữ nhật có các đặc điểm là:

A. Vuông góc với nhau

B. Bằng nhau

C. Cắt nhau tại trung điểm mỗi đường

D. Bằng nhau và cắt nhau tại trung điểm của mỗi đường.

Câu 1 2 . Hình 1 có tất cả nhiêu hình tam giác?

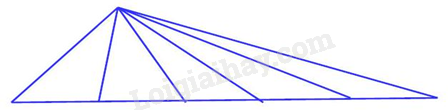
Hình a

A. 5 hình

B. 7 hình

C. 14 hình

D. 15 hình

Phần tự luận

Bài 1. Thực hiện phép tính (hợp lý nếu có thể):

a) $125 + 70 + 375 + 230$

b) ${4.5^2} - {3.2^3} + {7^5}:{7^3}$

c) $120:\left\{ {54 - \left[ {50:2 - \left( {{3^2} - 2.4} \right)} \right]} \right\}$

d) $46.\left( {2022 + 2.11} \right) + 54.\left( {2022 + 2.11} \right)$

Bài 2. Tìm số tự nhiên x biết:

a) $3.x + 27 = 162$

b) $3{\rm{x}} - 12 = {3^{2022}}:{3^{2020}}$

Bài 3 . Một nền nhà hình chữ nhật có chiều dài $8{\rm{\;m}}$, chiều rộng $4{\rm{\;m}}$.Tính chu vi và diện tích của nền nhà đó.

Bài 4 . Cho ${\rm{A}} = 1 + 3 + {3^2} +  \ldots  + {3^{2021}}$. Chứng tỏ rằng ${\rm{A}}$ chia hết cho 4.

-------- Hết --------

Lời giải

Phần trắc nghiệm

Câu 1. Trong các cách viết sau đây, cách viết đúng là:

A. $1,5 \in {\rm{N}}$

B. $0 \in {{\rm{N}}^{\rm{*}}}$

C. $0 \in {\rm{N}}$

D. $0 \notin {\rm{N}}$

Phương pháp:

Sử dụng kí hiệu $\in , \notin$.

Lời giải:

$0 \in {\rm{N}}$

Đáp án C.

Câu 2. Cho tập hợp $H = \left\{ {x \in {N^{\rm{*}}}\mid x \le 10} \right\}$. Số phần tử của tập hợp H là:

A. 9 phần tử

B. 10 phần tử

C. 11 phần tử

D. 12 phần tử

Phương pháp:

Liệt kê rồi đếm số phần tử của tập hợp.

Lời giải:

$H = \left\{ {1;2;3;4;5;6;7;8;9;10} \right\} \Rightarrow H$ gồm 10 phần tử.

Đáp án B.

Câu 3. Cho số 13 254 ta có:

A. Giá trị của chữ số 2 bằng nửa giá trị của chữ số 4

B. Giá trị của chữ số 2 bằng 5 lần giá trị của chữ số 4

C. Giá trị của chữ số 2 bằng 50 lần giá trị của chữ số 4

D. Giá trị của chữ số 2 bằng 500 lần giá trị của chữ số 4

Phương pháp:

Xác định giá trị của chữ số 2 và 4 rồi so sánh.

Lời giải:

Trong số 13 254, giá trị của chữ số 2 là 200, giá trị của chữ số 4 là 4.

Giá trị của chữ số 2 bằng 50 lần giá trị của chữ số 4.

Đáp án C.

Câu 4. Viết kết quả phép tính ${7^4}{.7^2}$ dưới dạng một lũy thừa ta được:

A. ${7^8}$

B. ${49^8}$

C. ${14^6}$

D. ${7^6}$

Phương pháp:

Áp dụng công thức nhân hai lũy thừa cùng cơ số.

Lời giải:

${7^4}{.7^2} = {7^{4 + 2}} = {7^6}$

Đáp án D.

Câu 5. Viết kết quả phép tính ${4^6}:{4^3}$ dưới dạng một lũy thừa ta được:

A. ${1^3}$

B. ${4^3}$

C. ${4^2}$

D. 4

Phương pháp:

Áp dụng công thức chia hai lũy thừa cùng cơ số.

Lời giải:

${4^6}:{4^3} = {4^{6 - 3}} = {4^3}$

Đáp án B.

Câu 6 . Cho 4 số tự nhiên: 1234; 3456; 5675; 7890. Số vừa chia hết cho 2, vừa chia hết cho 5 là:

A. 1234

B. 3456

C. 5675

D. 7890

Phương pháp:

Áp dụng dấu hiệu chia hết cho 2 và 5.

Lời giải:

Số chia hết cho 2 và 5 có chữ số tận cùng là 0.

Số 7890 vừa chia hết cho 2, vừa chia hết cho 5.

Đáp án D.

Câu 7 . Số các số nguyên tố nhỏ hơn 20 là:

A. 6 số

B. 7 số

C. 8 số

D. 9 số

Phương pháp:

Liệt kê và đếm số các số nguyên tố nhỏ hơn 20.

Lời giải:

Có 8 số nguyên tố nhỏ hơn 20 là: 2; 3; 5; 7; 11; 13; 17; 19.

Đáp án C.

Câu 8 . Trong các tổng dưới đây, tổng chia hết cho 7 là:

A. $14 + 35$

B. $21 + 15$

C. $17 + 49$

D. $70 + 27$

Phương pháp:

Áp dụng tính chất chia hết của một tổng.

Lời giải:

14 và 35 đều chia hết cho 7 nên $14 + 35 \vdots 7.$

Đáp án A.

Câu 9 . ƯCLN(6,8) là:

A. 48

B. 36

C. 24

D. 2

Phương pháp:

Vận dụng quy tắc tìm ƯCLN của hai hay nhiều số lớn hơn 1, ta thực hiện ba bước sau:

- Bước 1: Phân tích mỗi số ra thừa số nguyên tố.

- Bước 2: Chọn ra các thừa số nguyên tố chung.

- Bước 3: Lập tích các thừa số đã chọn, mỗi thừa số lấy với số mũ nhỏ nhất của nó.

Tích đó là ƯCLN phải tìm.

Lời giải:

Ta có: $6 = 2.3;\,\,8 = {2^3}$

Vậy ƯCLN $\left( {6;8} \right) = 2$

Đáp án D.

Câu 10 . Trong các hình sau đây, hình nào là hình lục giác đều?

A. Hình (1)

B. Hình (2)

C. Hình (3)

D. Hình (4)

Phương pháp:

Nhận biết hình lục giác đều.

Lời giải:

Hình (2) là hình lục giác đều.

Đáp án B.

Câu 1 1 . Hai đường chéo của hình chữ nhật có các đặc điểm là:

A. Vuông góc với nhau

B. Bằng nhau

C. Cắt nhau tại trung điểm mỗi đường

D. Bằng nhau và cắt nhau tại trung điểm của mỗi đường.

Phương pháp:

Sử dụng tính chất của hình chữ nhật.

Lời giải:

Hình chữ nhật có hai đường chéo bằng nhau và cắt nhau tại trung điểm của mỗi đường.

Đáp án D.

Câu 1 2 . Hình 1 có tất cả nhiêu hình tam giác?

Hình a

A. 5 hình

B. 7 hình

C. 14 hình

D. 15 hình

Phương pháp:

Đếm số tam giác.

Lời giải:

Có 15 hình tam giác trong hình a.

Đáp án D.

Phần tự luận.

Bài 1. Thực hiện phép tính (hợp lý nếu có thể):

a) $125 + 70 + 375 + 230$

b) ${4.5^2} - {3.2^3} + {7^5}:{7^3}$

c) $120:\left\{ {54 - \left[ {50:2 - \left( {{3^2} - 2.4} \right)} \right]} \right\}$

d) $46.\left( {2022 + 2.11} \right) + 54.\left( {2022 + 2.11} \right)$

Phương pháp:

Áp dụng các quy tắc thực hiện phép tính.

Lời giải:

$\begin{array}{l}{\rm{a) }}125 + 70 + 375 + 230\\ = (125 + 375) + (70 + 230)\\ = 500 + 300\\ = 800\end{array}$

$\begin{array}{l}{\rm{b) }}{4.5^2} - {3.2^3} + {7^5}:{7^3}\\ = 4.25 - 3.8 + {7^2}\\ = 100 - 24 + 49\\ = 76 + 49\\ = 125\end{array}$

$\begin{array}{l}{\rm{ c) }}120:\left\{ {54 - \left[ {50:2 - \left( {{3^2} - 2 \cdot 4} \right)} \right]} \right\}\\ = 120:\{ 54 - [50:2 - (9 - 8)]\} \\ = 120:\{ 54 - [25 - 1]\} \\ = 120:\{ 54 - 24\} \\ = 120:30\\ = 4\end{array}$

$\begin{array}{l}{\rm{ d) }}46.(2022 + 2.11) + 54.(2022 + 2.11)\\ = (2022 + 2.11).(46 + 54)\\ = (2022 + 22).100\\ = 2044.100\\ = 204400\end{array}$

Bài 2. Tìm số tự nhiên x biết:

a) $3.x + 27 = 162$

b) $3{\rm{x}} - 12 = {3^{2022}}:{3^{2020}}$

Phương pháp:

Áp dụng các quy tắc thực hiện phép tính.

Lời giải:

$\begin{array}{l}a){\rm{ }}3.x + 27 = 1623\\\,\,\,\,\,\,\,3.x{\rm{ }}\,\,\,\,\,\,\,\,\,\,\, = 162 - 273\\{\rm{ }}\,\,\,\,\,3.x{\rm{ }}\,\,\,\,\,\,\,\,\,\,\, = 135\\\,\,\,\,\,\,\,\,\,\,x\quad \,\,\,\,\,\,\, = 135:3\\\,\,\,\,\,\,\,\,\,\,x\quad \,\,\,\,\,\, = 45\quad \end{array}$

Vậy $x = 45.$

$\begin{array}{l}{\rm{b}})\,\,3x - 12 = {3^{2022}}:{3^{2020}}\\\,\,\,\,\,\,3x - 12 = {3^2}\\\,\,\,\,\,\,3x - 12 = 9\\\,\,\,\,\,\,3x\,\,\,\,\,\,\,\,\,\,\,\, = 9 + 12\\\,\,\,\,\,\,3x\quad \,\,\,\,\,\, = 21\\\,\,\,\,\,\,x\quad \,\,\,\,\,\,\,\,\, = 21:3\\\,\,\,\,\,\,x\quad \,\,\,\,\,\,\,\,\, = 7\end{array}$

Vậy $x = 7.$

Bài 3 . Một nền nhà hình chữ nhật có chiều dài $8{\rm{\;m}}$, chiều rộng $4{\rm{\;m}}$.Tính chu vi và diện tích của nền nhà đó.

Phương pháp:

Áp dụng công thức tính chu vi, diện tích hình chữ nhật.

Lời giải:

Chu vi của nền nhà là: $(8 + 4).2 = 24\,(\;{\rm{m}})$

Diện tích của nền nhà là: $8.4 = 32\left( {\;{{\rm{m}}^2}} \right)$

Bài 4 . Cho ${\rm{A}} = 1 + 3 + {3^2} +  \ldots  + {3^{2021}}$. Chứng tỏ rằng ${\rm{A}}$ chia hết cho 4.

Phương pháp:

Chia thành các nhóm, mỗi nhóm có hai số hạng.

Lời giải:

${\rm{A}} = {3^0} + 3 + {3^2} +  \ldots  + {3^{2021}}$

Ta có:

$\begin{array}{l}{\rm{A}} = (1 + 3) + \left( {{3^2} + {3^3}} \right) +  \ldots  + \left( {{3^{2020}} + {3^{2021}}} \right)\\ = 4 + {3^2}.(1 + 3) +  \ldots  + {3^{2020}}.(1 + 3)\\ = 4 + {3^2}.4 +  \ldots  + {3^{2020}}.4\\ = 4.\left( {1 + {3^2} +  \ldots  + {3^{2020}}} \right)\end{array}$

$4 \vdots 4$ và $\left( {1 + {3^2} +  \ldots  + {3^{2020}}} \right) \in {\rm{N}}\\ \Rightarrow 4.\left( {1 + {3^2} +  \ldots  + {3^{2020}}} \right) \vdots 4$

Vậy $A \vdots 4$.