Đề thi giữa kì 1 Toán 7 - Đề số 10 - Kết nối tri thức
Phần trắc nghiệm (3 điểm) Câu 1: Chọn đáp án đúng
Đề bài
Câu 1: Chọn đáp án đúng
A. \( - 7 \in \mathbb{N}\)
B. \( - 7 \notin \mathbb{Z}\)
C. \( - 7 \notin \mathbb{Q}\)
D. \(\frac{1}{2} \in \mathbb{Q}\)
Câu 2: Kết quả của phép tính: \(\frac{{ - 3}}{{20}} + \frac{{ - 2}}{{15}}\) là
A. \(\frac{{ - 1}}{{60}}\)
B. \(\frac{{ - 17}}{{60}}\)
C. \(\frac{{ - 5}}{{35}}\)
D. \(\frac{1}{{60}}\)
Câu 3: Kết quả của phép tính: - 0,35. \(\frac{2}{7}\) là
A. - 0,1
B. -1
C. -10
D. -100
Câu 4: Kết quả của phép tính: \(\frac{{ - 26}}{{15}}:2\frac{3}{5}\) là
A. -6
B. \(\frac{{ - 3}}{2}\)
C. \(\frac{{ - 2}}{3}\)
D. \(\frac{{ - 3}}{4}\)
Câu 5: Kết quả phép tính: \(\frac{3}{4} + \frac{1}{4}.\frac{{ - 12}}{{20}}\) là
A. \(\frac{{ - 12}}{{20}}\)
B. \(\frac{3}{5}\)
C. \(\frac{{ - 3}}{5}\)
D. \(\frac{{ - 9}}{{84}}\)
Câu 6: Giá trị của biểu thức : | - 3,4 | : | +1,7 | - 0,2 là
A. - 1,8
B. 1,8
C. 0
D. - 2,2
Câu 7: Kết quả phép tính: \({\left( { - \frac{1}{3}} \right)^4}\)
A. \(\frac{1}{{81}}\).
B. \(\frac{4}{{81}}\).
C. \(\frac{{ - 1}}{{81}}\).
D. \(\frac{{ - 4}}{{81}}\).
Câu 8: Quan sát trục số sau. Khẳng định nào sau đây đúng?

A. Điểm \(A\) biểu diễn số hữu tỉ \(\frac{1}{2}\).
B. Điểm \(B\) biểu diễn số hữu tỉ \(2\).
C. Điểm \(C\) biểu diễn số hữu tỉ \(\frac{1}{2}\).
D. Điểm A biểu diễn số hữu tỉ \(\frac{{ - 1}}{2}\).
Câu 9: Cho a\( \bot \)b và b \( \bot \)c thì
A. c//a
B. a//b//c
C. b//c
D. a\( \bot \)c
Câu 10: Nếu một đường thẳng a cắt hai đường thẳng song song b và c thì
A. Hai góc so le trong bằng nhau
B. Hai góc đồng vị bằng nhau
C. Hai góc trong cùng phía bù nhau
D. Cả ba ý trên
Câu 11 : Nội dung đúng của tiên đề ƠClít
A. Qua một điểm nằm ngoài đường thẳng a, có một đường thẳng song song với a
B. Qua một điểm nằm ngoài đường thẳng a, không có quá hai đường thẳng song song với a
C. Qua một điểm nằm ngoài đường thẳng a, chỉ có một đường thẳng song song với a
D. Qua một điểm nằm ngoài đường thẳng a, có nhiều hơn một đường thẳng song song với a
Câu 12: Cho hai đường thẳng a, b sao cho a // b, đường thẳng c \( \bot \) a. Khi đó:
A. c \( \bot \) b
B. c // b
C. c trùng với b
D. c cắt b
Phần tự luận (7 điểm)
Bài 1 : (2 điểm) Tìm x, biết
a. \(x - \frac{3}{4} = \frac{5}{{ - 7}}\)
b. 100 - \(\left| {x + 1} \right| = 90\);
Bài 2. (1,5 điểm) Thực hiện phép tính:
a) \(\frac{2}{3}:\frac{{ - 6}}{9} + \frac{1}{7}\);
b) \(\frac{{ - 3}}{{11}} \cdot \frac{5}{9} + \frac{4}{9} \cdot \frac{{ - 3}}{{11}}\);
c) \(\frac{{{9^5}{{.8}^2}}}{{{{27}^3}.16}}\).
Bài 3: (3 điểm) Vẽ lại hình sau
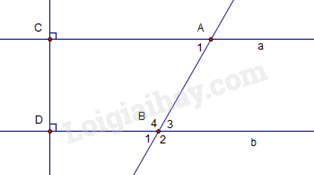
a. Hãy cho biết:
Góc đồng vị với \({\widehat A_1}\); Góc so le trong với \({\widehat A_1}\);
Góc trong cùng phía với \({\widehat A_1}\)là góc nào?
b. a và b có song song không? Vì sao ?
c. Cho \({\widehat A_1} = {60^0}\). Tính số đo các góc \({\widehat B_1};{\rm{ }}{\widehat B_2};{\rm{ }}{\widehat B_3};{\rm{ }}{\widehat B_4}\).
Bài 4. (0,5 điểm) Tìm hai số x, y. Tính giá trị nhỏ nhất của biểu thức: \({\rm{M}} = {({\rm{x}} - 5)^2} + 7\)
-------- Hết --------
Lời giải
Phần trắc nghiệm ( 3 điểm)
|
Câu 1: D |
Câu 2: B |
Câu 3: A |
Câu 4: C |
Câu 5: B |
Câu 6: B |
|
Câu 7. A |
Câu 8. A |
Câu 9. A |
Câu 10. D |
Câu 11. C |
Câu 12. A |
Câu 1: Chọn đáp án đúng
|
A. \( - 7 \in \mathbb{N}\) |
B. \( - 7 \notin \mathbb{Z}\) |
|
C. \( - 7 \notin \mathbb{Q}\) |
D. \(\frac{1}{2} \in \mathbb{Q}\) |
Phương pháp
Dựa vào các tập hợp số đã học.
Lời giải
Ta có:
\( - 7 \notin \mathbb{N}\) nên A sai.
\( - 7 \in \mathbb{Z}\) nên B sai.
\( - 7 \in \mathbb{Q}\) nên C sai.
\(\frac{1}{2} \in \mathbb{Q}\) nên D đúng.
Đáp án D.
Câu 2: Kết quả của phép tính: \(\frac{{ - 3}}{{20}} + \frac{{ - 2}}{{15}}\) là
|
A. \(\frac{{ - 1}}{{60}}\) |
B. \(\frac{{ - 17}}{{60}}\) |
|
C. \(\frac{{ - 5}}{{35}}\) |
D. \(\frac{1}{{60}}\) |
Phương pháp
Sử dụng quy tắc cộng hai số hữu tỉ.
Lời giải
\(\frac{{ - 3}}{{20}} + \frac{{ - 2}}{{15}} = \frac{{ - 9 + \left( { - 8} \right)}}{{60}} = \frac{{ - 17}}{{60}}\)
Đáp án B.
Câu 3: Kết quả của phép tính: - 0,35. \(\frac{2}{7}\) là
|
A. - 0,1 |
B. -1 |
|
C. -10 |
D. -100 |
Phương pháp
Sử dụng quy tắc nhân số hữu tỉ.
Lời giải
\( - {\rm{ }}0,35.\;\frac{2}{7} = - \frac{7}{{20}}.\frac{2}{7} = - \frac{1}{{10}} = - 0,1\).
Đáp án A.
Câu 4: Kết quả của phép tính: \(\frac{{ - 26}}{{15}}:2\frac{3}{5}\) là
|
A. -6 |
B. \(\frac{{ - 3}}{2}\) |
|
C. \(\frac{{ - 2}}{3}\) |
D. \(\frac{{ - 3}}{4}\) |
Phương pháp
Sử dụng quy tắc chia số hữu tỉ.
Lời giải
\(\frac{{ - 26}}{{15}}:2\frac{3}{5} = \frac{{ - 26}}{{15}}:\frac{{13}}{5} = \frac{{ - 26}}{{15}}.\frac{5}{{13}} = \frac{{ - 2}}{3}\)
Đáp án C.
Câu 5: Kết quả phép tính: \(\frac{3}{4} + \frac{1}{4}.\frac{{ - 12}}{{20}}\) là
|
A. \(\frac{{ - 12}}{{20}}\) |
B. \(\frac{3}{5}\) |
|
C. \(\frac{{ - 3}}{5}\) |
D. \(\frac{{ - 9}}{{84}}\) |
Phương pháp
Sử dụng các quy tắc tính với số hữu tỉ.
Lời giải
\(\frac{3}{4} + \frac{1}{4}.\frac{{ - 12}}{{20}} = \frac{3}{4} + \frac{{ - 3}}{{20}} = \frac{3}{5}\).
Đáp án B.
Câu 6: Giá trị của biểu thức : | - 3,4 | : | +1,7 | - 0,2 là
|
A. - 1,8 |
B. 1,8 |
|
C. 0 |
D. - 2,2 |
Phương pháp
Xác định giá trị tuyệt đối của -3,4 và +1,7 để tính toán.
Lời giải
| - 3,4 | : | +1,7 | - 0,2 = 3,4 : 1,7 – 0,2 = 2 – 0,2 = 1,8.
Đáp án B.
Câu 7: Kết quả phép tính: \({\left( { - \frac{1}{3}} \right)^4}\)
|
A. \(\frac{1}{{81}}\) . |
B. \(\frac{4}{{81}}\) . |
|
C. \(\frac{{ - 1}}{{81}}\) . |
D. \(\frac{{ - 4}}{{81}}\) . |
Phương pháp
Dựa vào cách tính lũy thừa của một số.
Lời giải
\({\left( { - \frac{1}{3}} \right)^4} = \frac{1}{{81}}\).
Đáp án A.
Câu 8: Quan sát trục số sau. Khẳng định nào sau đây đúng?

A. Điểm \(A\) biểu diễn số hữu tỉ \(\frac{1}{2}\).
B. Điểm \(B\) biểu diễn số hữu tỉ \(2\).
C. Điểm \(C\) biểu diễn số hữu tỉ \(\frac{1}{2}\).
D. Điểm A biểu diễn số hữu tỉ \(\frac{{ - 1}}{2}\).
Phương pháp
Quan sát trục số để xác định các điểm trên trục số.
Lời giải
Quan sát trục số ta thấy mỗi ô là 1 đơn vị nên các điểm biểu diễn các số sau:
Điểm A biểu diễn số hữu tỉ \(\frac{1}{2}\).
Điểm B biểu diễn số hữu tỉ 1.
Điểm C biểu diễn số hữu tỉ \(\frac{{ - 7}}{2}\).
Vậy đáp án đúng là A.
Đáp án A.
Câu 9: Cho a\( \bot \)b và b \( \bot \)c thì
|
A. c//a |
B. a//b//c |
|
C. b//c |
D. a\( \bot \)c |
Phương pháp
Dựa vào kiến thức về mối liên hệ giữa đường thẳng vuông góc và song song.
Lời giải
Vì a\( \bot \)b và b \( \bot \)c nên a // c.
Đáp án A.
Câu 10: Nếu một đường thẳng a cắt hai đường thẳng song song b và c thì
A. Hai góc so le trong bằng nhau
B. Hai góc đồng vị bằng nhau
C. Hai góc trong cùng phía bù nhau
D. Cả ba ý trên
Phương pháp
Dựa vào kiến thức về hai đường thẳng song song.
Lời giải
Nếu một đường thẳng a cắt hai đường thẳng song song b và c thì hai góc so le trong bằng nhau, hai góc đồng vị bằng nhau, hai góc trong cùng phía bù nhau.
Đáp án D.
Câu 11 : Nội dung đúng của tiên đề ƠClít
A. Qua một điểm nằm ngoài đường thẳng a, có một đường thẳng song song với a
B. Qua một điểm nằm ngoài đường thẳng a, không có quá hai đường thẳng song song với a
C. Qua một điểm nằm ngoài đường thẳng a, chỉ có một đường thẳng song song với a
D. Qua một điểm nằm ngoài đường thẳng a, có nhiều hơn một đường thẳng song song với a
Phương pháp
Dựa vào kiến thức về hai đường thẳng song song.
Lời giải
Qua một điểm nằm ngoài một đường thẳng a, chỉ có một đường thẳng song song với a.
Đáp án C.
Câu 12: Cho hai đường thẳng a, b sao cho a // b, đường thẳng c \( \bot \) a. Khi đó:
|
A. c \( \bot \) b |
B. c // b |
|
C. c trùng với b |
D. c cắt b |
Phương pháp
Dựa vào mối liên hệ giữa vuông góc và song song.
Lời giải
Nếu đường thẳng a // b, c \( \bot \) a thì c \( \bot \) b.
Đáp án A.
Phần tự luận.
Bài 1 : (2 điểm) . Tìm x, biết
|
a. \(x - \frac{3}{4} = \frac{5}{{ - 7}}\) |
b. 100 - \(\left| {x + 1} \right| = 90\) |
Phương pháp
Sử dụng quy tắc chuyển vế, kiến thức về giá trị tuyệt đối để giải tìm x.
Lời giải
a. \(x - \frac{3}{4} = \frac{5}{{ - 7}}\)
\(\begin{array}{l}x = \frac{5}{{ - 7}} + \frac{3}{4}\\x = \frac{1}{{28}}\end{array}\)
Vậy \(x = \frac{1}{{28}}\).
b. 100 - \(\left| {x + 1} \right| = 90\)
\(\begin{array}{l}|x + 1| = 100 - 90\\|x + 1| = 10\end{array}\)
=> x + 1 = 10 hoặc x + 1 = -10
hay x = 9 hoặc x = -11.
Vậy x = 9 hoặc x = -11.
Bài 2. (1,5 điểm). Thực hiện phép tính:
|
a) \(\frac{2}{3}:\frac{{ - 6}}{9} + \frac{1}{7}\); |
b) \(\frac{{ - 3}}{{11}} \cdot \frac{5}{9} + \frac{4}{9} \cdot \frac{{ - 3}}{{11}}\); |
c) \(\frac{{{9^5}{{.8}^2}}}{{{{27}^3}.16}}\). |
Phương pháp
Dựa vào quy tắc tính với số hữu tỉ và lũy thừa để tính.
Lời giải
a) \(\frac{2}{3}:\frac{{ - 6}}{9} + \frac{1}{7}\)
\( = \frac{2}{3}.\frac{{ - 9}}{6} + \frac{1}{7}\)\( = - 1 + \frac{1}{7}\)\( = \frac{{ - 6}}{7}\).
b) \(\frac{{ - 3}}{{11}} \cdot \frac{5}{9} + \frac{4}{9} \cdot \frac{{ - 3}}{{11}}\)
\( = \frac{{ - 3}}{{11}} \cdot \left( {\frac{5}{9} + \frac{4}{9}} \right)\)\( = \frac{{ - 3}}{{11}}.1\)\( = \frac{{ - 3}}{{11}}\).
c) \(\frac{{{9^5}{{.8}^2}}}{{{{27}^3}.16}}\)
\( = \frac{{{{\left( {{3^2}} \right)}^5}.{{\left( {{2^3}} \right)}^2}}}{{{{\left( {{3^3}} \right)}^3}{{.2}^4}}}\)\( = \frac{{{3^{10}}{{.2}^6}}}{{{3^9}{{.2}^4}}}\)\( = {3.2^2} = 3.4 = 12\)
Bài 3: (3 điểm) Vẽ lại hình sau
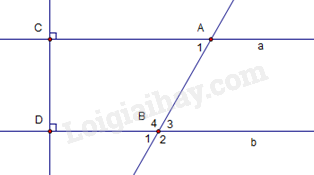
a. Hãy cho biết:
Góc đồng vị với \({\widehat A_1}\); Góc so le trong với \({\widehat A_1}\);
Góc trong cùng phía với \({\widehat A_1}\)là góc nào?
b. a và b có song song không? Vì sao ?
c. Cho \({\widehat A_1} = {60^0}\). Tính số đo các góc \({\widehat B_1};{\rm{ }}{\widehat B_2};{\rm{ }}{\widehat B_3};{\rm{ }}{\widehat B_4}\).
Phương pháp
a. Quan sát hình vẽ để xác định góc đồng vị, góc so le, góc trong cùng phía với \({\widehat A_1}\).
b. Chứng minh a và b có hai góc đồng vị bằng nhau nên song song.
c. Dựa vào tính chất góc tương ứng của hai đường thẳng song song, góc đối đỉnh để xác định số đo góc.
Lời giải
a. Góc đồng vị với \({\widehat A_1}\) là \({\widehat B_1}\);
Góc so le trong với \({\widehat A_1}\) là \({\widehat B_3}\);
Góc trong cùng phía với \({\widehat A_1}\) là \({\widehat B_4}\).
b. \(a \bot CD\) tại C (GT) và \(b \bot CD\) tại D (GT)
Suy ra a // b (tính chất từ vuông góc đến song song)
c. Vì a // b (câu b) nên \({\widehat B_1} = {\widehat A_1} = {60^0}\) (2 góc đồng vị)
\({\widehat B_3} = {\widehat B_1} = {60^0}\) ( 2 góc đối đỉnh)
\({\widehat B_2} = {180^0} - {\widehat B_1}\) (2 góc kề bù), suy ra \({\widehat B_2} = {120^0}\)
\({\widehat B_4} = {\widehat B_2} = {120^0}\) ( 2 góc đối đỉnh)
Bài 4. (0,5 điểm). Tìm hai số x, y. Tính giá trị nhỏ nhất của biểu thức: \({\rm{M}} = {({\rm{x}} - 5)^2} + 7\)
Phương pháp
Dựa vào đặc điểm của biểu thức (x – 5) 2 .
Lời giải
Ta có \({\left( {x - 5} \right)^2} \ge 0,\,\forall x \in \mathbb{R}\) nên \({\left( {x - 5} \right)^2} + 7 \ge 7,\,\forall x \in \mathbb{R}\) hay \(M \ge 7\). Dấu “=” xảy ra khi và chỉ khi \({\left( {x - 5} \right)^2} = 0 \Leftrightarrow x = 5\).
Vậy giá trị nhỏ nhất của M là 7 khi x = 5.