Đề thi giữa kì 1 Toán 7 Kết nối tri thức - Đề số 12 — Không quảng cáo

Dựa vào kiến thức về các tập hợp \(\mathbb{N},\mathbb{Z},\mathbb{R},\mathbb{Q}\).

\( - 9\) không phải số tự nhiên nên \( - 9 \in \mathbb{N}\) là khẳng định sai.

\(\frac{7}{3}\) không phải số nguyên nên \(\frac{7}{3} \in \mathbb{Z}\) là khẳng định sai.

\(1,2\) là số thực nên khẳng định \(1,2 \notin \mathbb{R}\) là khẳng định sai.

\(\frac{{ - 5}}{2}\) là số hữu tỉ nên \(\frac{{ - 5}}{2} \in \mathbb{Q}\) là khẳng định đúng.

Đáp án D.

Số hữu tỉ dương là các số viết được dưới dạng phân số và lớn hơn 0.

Có 3 số hữu tỉ dương, đó là: \(\frac{{ - 7}}{{ - 15}};0,2;\frac{{13}}{5}\).

Vì \(\frac{{ - 7}}{{ - 15}} = \frac{7}{{15}}\); \(0,2 = \frac{2}{{10}} = \frac{1}{5}\) và \(\frac{{13}}{5}\) đều là số hữu tỉ.

Đáp án C.

Số đối của số hữu tỉ a là – a.

Số đối của \(\frac{{ - 2}}{3}\) là: \( - \left( {\frac{{ - 2}}{3}} \right) = \frac{2}{3}\).

Đáp án A.

Khi \(\left| x \right| = k > 0\) thì xảy ra hai trường hợp: \(x = k\) hoặc \(x =  - k\).

Ta có: \(\left| x \right| = 3\) nên \(x = 3\) hoặc \(x =  - 3\).

Đáp án C.

Khi nhân 2 lũy thừa cùng cơ số, ta giữ nguyên cơ số và cộng 2 số mũ:

\({x^m}.{x^n} = {x^{m + n}}\).

Ta có: \({2^2}{.2^5} = {2^{2 + 5}} = {2^7}\).

Đáp án D.

Căn bậc hai số học của một số a không âm, kí hiệu \(\sqrt a \),  là số x không âm sao cho \({x^2} = a\).

Căn bậc hai số học của 64 là: \(\sqrt {64}  = \sqrt {{8^2}}  = 8\).

* Lưu ý: -8 không phải là căn bậc hai số học của 64.

Đáp án D.

Số vô tỉ là số viết được dưới dạng số thập phân vô hạn không tuần hoàn.

\(\sqrt {{5^2}} \) không phải số vô tỉ vì \(\sqrt {{5^2}}  = 5\).

\(\sqrt 3 \) là số vô tỉ.

\(\sqrt {{{\left( {3,5} \right)}^2}} \) không phải số vô tỉ vì \(\sqrt {{{\left( {3,5} \right)}^2}}  = 3,5\).

\(\sqrt {16} \) không phải số vô tỉ vì \(\sqrt {16}  = \sqrt {{4^2}}  = 4\).

Đáp án B.

Làm tròn số với độ chính xác:

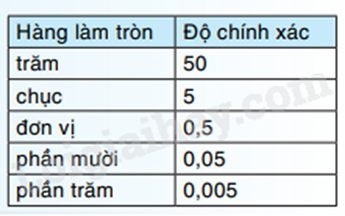
Làm tròn số \(5,16578\) với độ chính xác 0,005, tức là làm tròn số \(5,16578\) đến hàng phần trăm, ta được \(5,17\).

Đáp án A.

Dựa vào kiến thức về hai góc kề bù: Hai góc kề bù có tổng là \(180^\circ \).

Vì \(\widehat {BOC}\) và \(\widehat {COA}\) là hai góc kề bù nên ta có: \(\widehat {BOC} + \widehat {COA} = 180^\circ \).

Suy ra \(\widehat {BOC} = 180^\circ  - \widehat {COA} = 180^\circ  - 120^\circ  = 60^\circ \).

Đáp án A.

Dựa vào kiến thức về tính chất hai đường thẳng song song.

Vì a // b nên \(x = 65^\circ \) (hai góc so le trong).

Đáp án C.

Áp dụng tiên đề Euclid về đường thẳng song song.

Theo tiên đề Euclid ta có: Qua điểm M ở ngoài đường thẳng a cho trước, vẽ được duy nhất một đường thẳng song song với đường thẳng đó.

Đáp án D.

Hai đường thẳng phân biệt cùng vuông góc với một đường thẳng thứ ba thì chúng song song với nhau.

Vì \(a \bot c\) và \(c \bot b\) nên a // b.

Đáp án B.

Dựa vào quy tắc thực hiện phép tính với số hữu tỉ, giá trị tuyệt đối và căn bậc hai để thực hiện.

a) \(\frac{9}{8} - \frac{1}{8}:\frac{3}{4}\) \( = \frac{9}{8} - \frac{1}{8}.\frac{4}{3}\) \( = \frac{9}{8} - \frac{1}{6}\) \( = \frac{{23}}{{24}}\).

b) \(\frac{{23}}{{25}} - \frac{{19}}{{43}} + \frac{{27}}{{25}} - \frac{{24}}{{43}}\) \( = \left( {\frac{{23}}{{25}} + \frac{{27}}{{25}}} \right) - \left( {\frac{{19}}{{43}} + \frac{{24}}{{43}}} \right)\) \( = 2 - 1\) \( = 1\).

c) \(\frac{2}{5}.\frac{{ - 17}}{9} + \frac{2}{5}.\left| {\frac{{ - 8}}{9}} \right| - \sqrt {16} \) \( = \frac{2}{5}.\frac{{ - 17}}{9} + \frac{2}{5}.\frac{8}{9} - 4\) \( = \frac{2}{5}.\left( {\frac{{ - 17}}{9} + \frac{8}{9}} \right) - 4\) \( = \frac{2}{5}.\left( { - 1} \right) - 4\) \( = \frac{{ - 2}}{5} - 4\) \( = \frac{{ - 22}}{5}\).

a, b) Sử dụng quy tắc chuyển vế và thực hiện phép tính để tìm x.

c) Chuyển vế, sử dụng kiến thức \(\left| A \right| = k > 0\) thì xảy ra hai trường hợp: \(A = k\) hoặc \(A =  - k\).

a) \(x + 4,5 = 9,5\)

\(x = 9,5 - 4,5\)

\(x = 5\)

Vậy \(x = 5\).

b) \(\frac{7}{5}x - \frac{1}{2} = \frac{3}{8}\)

\(\begin{array}{l}\frac{7}{5}x = \frac{3}{8} + \frac{1}{2}\\\frac{7}{5}x = \frac{7}{8}\\x = \frac{7}{8}:\frac{7}{5}\\x = \frac{7}{8}.\frac{5}{7}\\x = \frac{5}{8}\end{array}\)

Vậy \(x = \frac{5}{8}\).

c) \(\left| {3x - 1} \right| + \frac{1}{3} = \frac{1}{2}\)

\(\begin{array}{l}\left| {3x - 1} \right| = \frac{1}{2} - \frac{1}{3}\\\left| {3x - 1} \right| = \frac{1}{6}\end{array}\)

Suy ra \(3x - 1 = \frac{1}{6}\) hoặc \(3x - 1 = \frac{{ - 1}}{6}\)

TH1: \(3x - 1 = \frac{1}{6}\)

\(\begin{array}{l}3x = \frac{1}{6} + 1\\3x = \frac{7}{6}\\x = \frac{7}{6}:3\\x = \frac{7}{{18}}\end{array}\)

TH2: \(3x - 1 = \frac{{ - 1}}{6}\)

\(\begin{array}{l}3x =  - \frac{1}{6} + 1\\3x = \frac{5}{6}\\x = \frac{5}{6}:3\\x = \frac{5}{{18}}\end{array}\)

Vậy \(x = \frac{7}{{18}};x = \frac{5}{{18}}\).

Áp dụng quy tắc cộng, trừ với số thực.

Khối lượng chất khác trong 100g khoai tây khô là:

\(100 - 11 - 6,6 - 0,3 - 75,1 = 89 - \left( {6,6 + 0,3 + 75,1} \right) = 89 - 82 = 7\left( g \right)\)

Khối lượng chất khác trong 300g khoai tây khô là:

\(7.3 = 21\left( g \right)\)

Vậy khối lượng chất khác trong 300g khoai tây khô là 21g.

a) Sử dụng dấu hiệu nhận biết hai đường thẳng song song: Hai đường thẳng phân biệt cùng vuông góc với một đường thẳng thứ ba thì chúng song song với nhau.

b) Sử dụng tính chất của hai đường thẳng song song: hai góc đồng vị bằng nhau.

Hai góc kề bù thì tổng của chúng bằng \(180^\circ \).

c) Sử dụng kiến thức về tia phân giác của một góc.

Sử dụng dấu hiệu nhận biết hai đường thẳng song song (hai góc bằng nhau ở vị trí đồng vị)

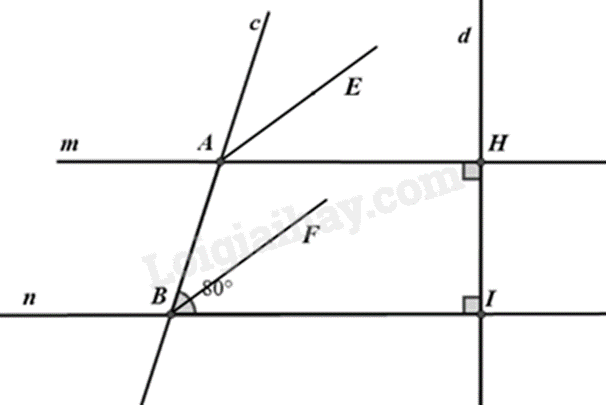
a) Ta có: \(m \bot d;n \bot d\) nên m // n (tính chất hai đường thẳng song song).

b) Vì m // n nên \(\widehat {cAH} = \widehat {ABI} = 80^\circ \) (hai góc đồng vị).

Vì \(\widehat {mAc}\) và \(\widehat {cAH}\) là hai góc kề bù nên ta có \(\widehat {mAc} + \widehat {cAH} = 180^\circ \)

Suy ra \(\widehat {mAc} = 180^\circ  - \widehat {cAH} = 180^\circ  - 80^\circ  = 100^\circ \).

Vậy \(\widehat {cAH} = 80^\circ ;\widehat {mAc} = 100^\circ \).

c) Vì AE là tia phân giác của \(\widehat {cAH}\) nên \(\widehat {cAE} = \frac{1}{2}\widehat {cAH} = \frac{{80^\circ }}{2} = 40^\circ \).

Tương tự, ta tính được \(\widehat {ABF} = 40^\circ \).

Ta có \(\widehat {cAE} = \widehat {ABF} = 40^\circ \).

Mà hai góc này là hai góc ở vị trí đồng vị nên AE // BF.

Đặt \(A = \frac{1}{{{3^2}}} + \frac{1}{{{3^4}}} + \frac{1}{{{3^6}}} + ... + \frac{1}{{{3^{802}}}}\)

Nhân hai vế của \(A\) với \({3^2}\).

Lấy \({3^2}A - A\), so sánh với 1 để chứng minh \(A < \frac{1}{8}\).

Từ đó chứng minh \(M = \frac{1}{{{2^2}}} + A < \frac{3}{8}\)

Đặt \(A = \frac{1}{{{3^2}}} + \frac{1}{{{3^4}}} + \frac{1}{{{3^6}}} + ... + \frac{1}{{{3^{802}}}}\)

Ta có: \({3^2}.A = {3^2}.\left( {\frac{1}{{{3^2}}} + \frac{1}{{{3^4}}} + \frac{1}{{{3^6}}} + ... + \frac{1}{{{3^{802}}}}} \right)\)

\(9A = 1 + \frac{1}{{{3^2}}} + \frac{1}{{{3^4}}} + \frac{1}{{{3^6}}} + ... + \frac{1}{{{3^{800}}}}\)

Suy ra

\(9A - A = \left( {1 + \frac{1}{{{3^2}}} + \frac{1}{{{3^4}}} + \frac{1}{{{3^6}}} + ... + \frac{1}{{{3^{800}}}}} \right) - \left( {\frac{1}{{{2^2}}} + \frac{1}{{{3^2}}} + \frac{1}{{{3^4}}} + \frac{1}{{{3^6}}} + ... + \frac{1}{{{3^{802}}}}} \right)\)

\(8A = 1 - \frac{1}{{{3^{802}}}}\)

Vì \(1 - \frac{1}{{{3^{802}}}} < 1\) nên \(8A < 1\), suy ra \(A < \frac{1}{8}\).

Mà \(M = \frac{1}{{{2^2}}} + A < \frac{1}{4} + \frac{1}{8} = \frac{3}{8}\) nên \(M < \frac{3}{8}\).

Vậy \(M < \frac{3}{8}\).