Đề thi giữa kì 1 Toán 8 - Đề số 1 - Kết nối tri thức
Phần trắc nghiệm (4 điểm) Câu 1: Tìm hệ số trong đơn thức ( - 36{a^2}{b^2}{x^2}{y^3}) với a,b là hằng số.
Đề bài
Phần trắc nghiệm ( 4 điểm)
Câu 1: Tìm hệ số trong đơn thức \( - 36{a^2}{b^2}{x^2}{y^3}\) với a,b là hằng số.
A. \( - 36\)
B. \( - 36{a^2}{b^2}\)
C. \(36{a^2}{b^2}\)
D. \( - 36{a^2}\)
Câu 2: Giá trị của đa thức \(4{x^2}y - \frac{2}{3}x{y^2} + 5xy - x\) tại \(x = 2;y = \frac{1}{3}\) là
A. \(\frac{{176}}{{27}}\)
B. \(\frac{{27}}{{176}}\)
C. \(\frac{{17}}{{27}}\)
D. \(\frac{{116}}{{27}}\)
Câu 3: Chọn câu sai.
Câu 4: Có bao nhiêu giá trị \(x\) thỏa mãn \({\left( {2x - 1} \right)^2} - {\left( {5x - 5} \right)^2} = 0\)
A. \(0\)
B. \(1\)
C. \(2\)
D. \(3\)
Câu 5: Chọn câu đúng .
Câu 6: Tứ giác ABCD có \(AB = BC,CD = DA,\;\hat B = {90^0};\;\hat D = {120^0}\). Hãy chọn câu đúng nhất :
A. \(\hat A = {85^0}\).
B. \(\hat C = {75^0}\).
C. \(\hat A = {75^0}\).
D. Chỉ \(B\) và \(C\) đúng.
Câu 7: Hình thang ABCD (AB//CD) có số đo góc D bằng \({70^0},\) số đo góc \(A\) là:
A. \({130^0}\)
B. \({90^0}\)
C. \({110^\circ }\)
D. \({120^0}\)
Câu 8: Chọn câu trả lời đúng . Tứ giác nào có hai đường chéo vuông góc với nhau?
A. Hình thoi
B. Hình vuông
C. Hình chữ nhật
D. Cả A và B.
Phần tự luận ( 6 điểm)
Bài 1. (1,5 điểm) Cho biểu thức: \(A = 3x(2x - y) + (x - y)(x + y) - 7{x^2} + {y^2}\).
a) Thu gọn A.
b) Tính giá trị của A biết x = \(\frac{{ - 2}}{3}\) và y = 2
Bài 2. (1,5 điểm) Tìm x biết:
a) \({\left( {x - 3} \right)^2} - {x^2} = 0\)
b) \({x^3} - 5{x^2} - 9x + 45 = 0\)
c) \(\left( {5x - 3} \right)\left( {2x + 1} \right) - {\left( {2x - 1} \right)^2} + 4 = 0\)
Bài 3. (2,5 điểm) Cho tam giác \(ABC\) vuông tại \(A\), đường trung tuyến \(AM\). Gọi \(H\) là điểm đối xứng với \(M\) qua \(AB\), \(E\) là giao điểm của \(MH\) và \(AB\). Gọi \(K\) là điểm đối xứng với \(M\) qua \(AC\), \(F\) là giao điểm của \(MK\) và \(AC\).
a) Các tứ giác \(AEMF\), \(AMBH\), \(AMCK\) là hình gì? Vì sao?
b) Chứng minh rằng \(H\) đối xứng với \(K\) qua \(A\).
c) Tam giác vuông \(ABC\) cần thêm điều kiện gì thì tứ giác \(AEMF\) là hình vuông?
Bài 4. (0,5 điểm) Cho a + b + c. Chứng minh \({a^3} + {b^3} + {c^3} = 3abc\).
Lời giải
Phần trắc nghiệm ( 4 điểm)
|
Câu 1: B |
Câu 2: A |
Câu 3: D |
Câu 4: C |
Câu 5: B |
Câu 6: D |
Câu 7: C |
Câu 8: D |
Câu 1: Tìm hệ số trong đơn thức \( - 36{a^2}{b^2}{x^2}{y^3}\) với a,b là hằng số.
|
A. \( - 36\) |
B. \( - 36{a^2}{b^2}\) |
|
C. \(36{a^2}{b^2}\) |
D. \( - 36{a^2}\) |
Phương pháp
Sử dụng lý thuyết về đơn thức thu gọn:
Đơn thức thu gọn là đơn thức chỉ gồm tích của một số với các biến mà mỗi biến đã được nâng lên lũy thừa với số mũ nguyên dương. Số nói trên gọi là hệ số, phần còn lại gọi là phần biến của đơn thức thu gọn.
Lời giải
Đơn thức \( - 36{a^2}{b^2}{x^2}{y^3}\) với a,b là hằng số có hệ số là \( - 36{a^2}{b^2}.\)
Đáp án B.
Câu 2: Giá trị của đa thức \(4{x^2}y - \frac{2}{3}x{y^2} + 5xy - x\) tại \(x = 2;y = \frac{1}{3}\) là
|
A. \(\frac{{176}}{{27}}\) |
B. \(\frac{{27}}{{176}}\) |
|
C. \(\frac{{17}}{{27}}\) |
D. \(\frac{{116}}{{27}}\) |
Phương pháp
Thay \(x = 2;y = \frac{1}{3}\) vào đa thức rồi tính toán.
Lời giải
Thay \(x = 2;y = \frac{1}{3}\) vào đa thức \(4{x^2}y - \frac{2}{3}x{y^2} + 5xy - x\) ta được \({4.2^2}.\frac{1}{3} - \frac{2}{3}.2.{\left( {\frac{1}{3}} \right)^2} + 5.2.\frac{1}{3} - 2\)\( = \frac{{176}}{{27}}\).
Đáp án A.
Câu 3:
Chọn câu sai.
Phương pháp
Sử dụng các công thức \({\left( {A + B} \right)^2} = {A^2} + 2AB + {B^2}\), \({\left( {A - B} \right)^2} = {A^2} - 2AB + {B^2}\) , \({A^2} - {B^2} = \left( {A - B} \right)\left( {A + B} \right)\)
Lời giải
Ta có \(\left( {x + y} \right)\left( {x + y} \right) = {\left( {x + y} \right)^2} = {x^2} + 2xy + {y^2} \ne {y^2} - {x^2}\) nên câu D sai.
Đáp án D.
Câu 4: Có bao nhiêu giá trị \(x\) thỏa mãn \({\left( {2x - 1} \right)^2} - {\left( {5x - 5} \right)^2} = 0\)
|
A. \(0\) |
B. \(1\) |
|
C. \(2\) |
D. \(3\) |
Phương pháp
Sử dụng công thức \({A^2} - {B^2} = \left( {A - B} \right)\left( {A + B} \right)\) để đưa về dạng tìm \(x\) thường gặp
Lời giải
Ta có \({\left( {2x - 1} \right)^2} - {\left( {5x - 5} \right)^2} = 0\)\( \Leftrightarrow \left( {2x - 1 + 5x - 5} \right)\left( {2x - 1 - 5x + 5} \right) = 0\)\( \Leftrightarrow \left( {7x - 6} \right)\left( {4 - 3x} \right) = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{7x - 6 = 0}\\{4 - 3x = 0}\end{array}} \right.\)
\( \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{x = \frac{6}{7}}\\{x = \frac{4}{3}}\end{array}} \right.\)
Vậy có hai giá trị của \(x\) thỏa mãn yêu cầu.
Đáp án C.
Câu 5:
Chọn câu đúng .
Phương pháp
Sử dụng công thức lập phương của một tổng \({\left( {A + B} \right)^3}\)\( = {A^3} + 3{A^2}B + 3A{B^2} + {B^3}\) và lập phương của một hiệu
\({\left( {A - B} \right)^3}\)\( = {A^3} - 3{A^2}B + 3A{B^2} - {B^3}\)
Lời giải
Ta có \(8 + 12y + 6{y^2} + {y^3}\)\( = {2^3} + {3.2^2}y + 3.2.{y^2} + {y^3}\)\( = {\left( {2 + y} \right)^3} \ne \left( {8 + {y^3}} \right)\) nên A sai.
+ Xét \({\left( {2x - y} \right)^3}\)\( = {\left( {2x} \right)^3} - 3.{\left( {2x} \right)^2}.y + 3.2x.{y^2} - {y^3}\)\( = 8{x^3} - 12{x^2}y + 6xy - {y^3}\)\( \ne 2{x^3} - 6{x^2}y + 6xy - {y^3}\) nên C sai.
+ Xét \({\left( {3a + 1} \right)^3}\)\( = {\left( {3a} \right)^3} + 3.{\left( {3a} \right)^2}.1 + 3.3a{.1^2} + 1\)\( = 27{a^3} + 27{a^2} + 9a + 1\)\( \ne 3{a^3} + 9{a^2} + 3a + 1\) nên D sai
Đáp án B.
Câu 6: Tứ giác ABCD có \(AB = BC,CD = DA,\;\hat B = {90^0};\;\hat D = {120^0}\). Hãy chọn câu đúng nhất :
|
A. \(\hat A = {85^0}\). |
B. \(\hat C = {75^0}\). |
|
C. \(\hat A = {75^0}\). |
D. Chỉ \(B\) và \(C\) đúng. |
Phương pháp
Ta sử dụng tính chất tam giác vuông cân , tam giác cân và tổng ba góc trong tam giác bằng \({180^\circ }\) .
Lời giải
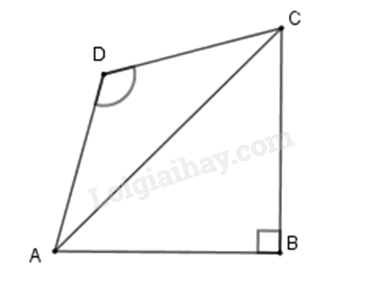
Xét tam giác ABC có \(\hat B = {90^\circ };AB = BC \Rightarrow \Delta ABC\) vuông cân \( \Rightarrow \widehat {BAC} = \widehat {BCA} = \frac{{{{90}^\circ }}}{2} = {45^\circ }\)
Xét tam giác ADC có \(CD = DA \Rightarrow \Delta ADC\) cân tại \(D\) có \(\widehat {ADC} = {120^\circ }\) nên \(\widehat {DAC} = \widehat {DCA} = \frac{{{{180}^\circ }{\rm{\;}} - {{120}^\circ }}}{2} = {30^\circ }\)
Từ đó ta có \(\hat A = \widehat {BAD} = \widehat {BAC} + \widehat {CAD} = {45^\circ }{\rm{\;}} + {30^\circ }{\rm{\;}} = {75^\circ }\)
Và \(\hat C = \widehat {BCD} = \widehat {BCA} + \widehat {ACD} = {45^\circ }{\rm{\;}} + {30^\circ }{\rm{\;}} = {75^\circ }\)
Nên \(\hat A = \hat C = {75^\circ }\) .
Đáp án D.
Câu 7: Hình thang ABCD (AB//CD) có số đo góc D bằng \({70^0},\) số đo góc \(A\) là:
|
A. \({130^0}\) |
B. \({90^0}\) |
|
C. \({110^\circ }\) |
D. \({120^0}\) |
Phương pháp
Ta sử dụng tính chất của hình thang: Ta thấy góc \(A\) và \(D\) là hai góc trong cùng phía nên \(\hat A + \hat D = {180^0}\) từ đó ta suy ra số đo góc A.
Lời giải
\(\hat A + \hat D = {180^0}\)
\(\begin{array}{*{20}{l}}{ \Rightarrow \hat A = {{180}^0} - \hat D}\\{{\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} = {{180}^0} - {{70}^0}}\\{{\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} = {{110}^0}}\end{array}\)
Đáp án C.
Câu 8: Chọn câu trả lời đúng . Tứ giác nào có hai đường chéo vuông góc với nhau?
|
A. Hình thoi |
B. Hình vuông |
|
C. Hình chữ nhật |
D. Cả A và B . |
Phương pháp
Dựa vào tính chất của các hình đã học.
Lời giải
Hình thoi và hình vuông đều có hai đường chéo vuông góc với nhau.
Đáp án D.
Phần tự luận.
Bài 1. (1,5 điểm) Cho biểu thức: \(A = 3x(2x - y) + (x - y)(x + y) - 7{x^2} + {y^2}\).
a) Thu gọn A.
b) Tính giá trị của A biết x = \(\frac{{ - 2}}{3}\) và y = 2
Phương pháp
a) Sử dụng quy tắc cộng, trừ, nhân, chia đa thức và những hằng đẳng thức đáng nhớ để rút gọn.
b) Thay x, y vào A để tính giá trị.
Lời giải
a) \(A = 3x(2x - y) + (x - y)(x + y) - 7{x^2} + {y^2}\)
\(\begin{array}{l} = 6{x^2} - 3xy + {x^2} - {y^2} - 7{x^2} + {y^2}\\ = - 3xy\end{array}\)
b) Thay x = \(\frac{{ - 2}}{3}\) và y = 2 vào A, ta được:
\(A = - 3.\left( {\frac{{ - 2}}{3}} \right).2 = 1\).
Vậy A = -3xy, giá trị của A tại x = \(\frac{{ - 2}}{3}\) và y = 2 là 1.
Bài 2. (1,5 điểm) Tìm x biết:
a) \({\left( {x - 3} \right)^2} - {x^2} = 0\)
b) \({x^3} - 5{x^2} - 9x + 45 = 0\)
c) \(\left( {5x - 3} \right)\left( {2x + 1} \right) - {\left( {2x - 1} \right)^2} + 4 = 0\)
Phương pháp
Dựa vào các hằng đẳng thức đáng nhớ, phân tích đa thức thành nhân tử để tìm x.
Lời giải
a) \({\left( {x - 3} \right)^2} - {x^2} = 0\)
\(\begin{array}{l}(x - 3 - x)(x - 3 + x) = 0\\ - 3.(2x - 3) = 0\\2x - 3 = 0\\x = \frac{3}{2}\end{array}\)
Vậy \(x = \frac{3}{2}\)
b) \({x^3} - 5{x^2} - 9x + 45 = 0\)
\(\begin{array}{l}{x^2}(x - 5) - 9(x - 5) = 0\\({x^2} - 9)(x - 5) = 0\\(x - 3)(x + 3)(x - 5) = 0\\\left[ \begin{array}{l}x - 3 = 0\\x + 3 = 0\\x - 5 = 0\end{array} \right.\\\left[ \begin{array}{l}x = 3\\x = - 3\\x = 5\end{array} \right.\end{array}\)
Vậy x =3, x = -3 hoặc x = 5.
c) \(\left( {5x - 3} \right)\left( {2x + 1} \right) - {\left( {2x - 1} \right)^2} + 4 = 0\)
\(\begin{array}{l}\left( {5x - 3} \right)\left( {2x + 1} \right) - {\left( {2x - 1} \right)^2} + 4 = 0\\\left( {5x - 3} \right)\left( {2x + 1} \right) - \left[ {\left( {2x - 1} \right) - 4} \right] = 0\\\left( {5x - 3} \right)\left( {2x + 1} \right) - \left( {2x - 1 - 2} \right)\left( {2x - 1 + 2} \right) = 0\\\left( {5x - 3} \right)\left( {2x + 1} \right) - \left( {2x - 3} \right)\left( {2x + 1} \right) = 0\\\left( {5x - 3 - 2x + 3} \right)\left( {2x + 1} \right) = 0\\3x\left( {2x + 1} \right) = 0\\\left[ \begin{array}{l}x = 0\\2x + 1 = 0\end{array} \right.\\\left[ \begin{array}{l}x = 0\\x = - \frac{1}{2}\end{array} \right.\end{array}\)
Vậy x = 0 hoặc x = \( - \frac{1}{2}\).
Bài 3. (2,5 điểm) Cho tam giác \(ABC\) vuông tại A, đường trung tuyến \(AM\). Gọi \(H\) là điểm đối xứng với \(M\) qua \(AB\), \(E\) là giao điểm của \(MH\) và \(AB\). Gọi \(K\) là điểm đối xứng với \(M\) qua \(AC\), \(F\) là giao điểm của \(MK\) và \(AC\).
a) Các tứ giác \(AEMF\), \(AMBH\), \(AMCK\) là hình gì? Vì sao?
b) Chứng minh rằng \(H\) đối xứng với \(K\) qua \(A\).
c) Tam giác vuông \(ABC\) cần thêm điều kiện gì thì tứ giác \(AEMF\) là hình vuông?
Phương pháp
a) Dựa vào dấu hiệu nhận biết các hình đã học.
b) Theo a) suy ra \(HA\parallel BM\), \(AK\parallel MC\) \( \Rightarrow \) \(H\), \(A\), \(K\) thẳng hàng.
Lại có \(AH = AM = AK\) \( \Rightarrow \) \(H\), \(K\) đối xứng với nhau qua \(A\).
c) Để hình chữ nhật \(AEMF\) là hình vuông thì cần thêm điều kiện \(AE = EM\). \( \Rightarrow \) \(AB = AC\). Vậy tam giác \(ABC\) vuông cân tại \(A\).
Lời giải
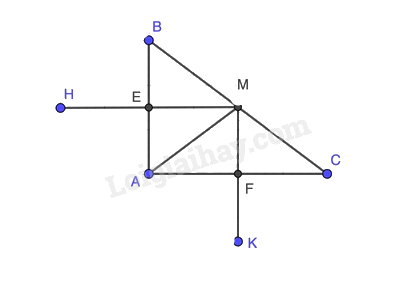
a)
+ Tứ giác AEMF:
Ta có:
\(\begin{array}{l}\widehat {MFA} = {90^0}(do\,MF \bot AC)\\\widehat {FAE} = {90^0}(gt)\\\widehat {MEA} = {90^0}(do\,ME \bot AB)\end{array}\)
=> AEMF là hình chữ nhật.
+ Tứ giác AMBH:
Tam giác ABC vuông tại A có AM là đường trung tuyến => AM = MB = MC = \(\frac{1}{2}BC\).
=> Tam giác AMB cân tại M.
Vì ME \( \bot \) AB => E là trung điểm của AB. => AE = EB.
Mà MH \( \bot \) AB tại E.
=> AMBH là hình thoi.
Chứng minh tương tự, ta cũng có AMCK là hình thoi.
b) Vì AMCK là hình thoi => AK // CM, AK = CM.
Tương tự, ta cũng có AH // BM, AH = BM.
=> K, A, H thẳng hàng và AK = AH = BM = CM.
=> H đối xứng với K qua A.
c) Để AEMF là hình vuông thì AE = MF, mà AE = \(\frac{1}{2}\)AB.
ME = \(\frac{1}{2}\)AC.
=> AB = AC hay tam giác ABC vuông cân tại A thì AEMF là hình vuông.
Bài 4. (0,5 điểm) Cho a + b + c. Chứng minh \({a^3} + {b^3} + {c^3} = 3abc\).
Phương pháp
Dựa vào hằng đẳng thức \({\left( {a + b} \right)^3} = {a^3} + 3{a^2}b + 3a{b^2} + {b^3}\) để suy ra \({(a + b + c)^3}\). Thay a + b + c = 0 để chứng minh.
Lời giải
Vì \(a + b + c = 0\) nên \({\left( {a + b + c} \right)^3} = 0\).
Phân tích \({\left( {a + b + c} \right)^3}\) ta được \({\left( {a + b + c} \right)^3} = {a^3} + {b^3} + {c^3} + 3{a^2}b + 3a{b^2} + 3{b^2}c + 3b{c^2} + 3{a^2}c + 3a{c^2} + 6abc\)
\( = > {a^3} + {b^3} + {c^3} + 3{a^2}b + 3a{b^2} + 3{b^2}c + 3b{c^2} + 3{a^2}c + 3a{c^2} + 6abc = 0\)
\( = > {a^3} + {b^3} + {c^3} + \left( {3{a^2}b + 3a{b^2} + 3abc} \right) + \left( {3{b^2}c + 3b{c^2} + 3abc} \right) + \left( {3{a^2}c + 3a{c^2} + 3abc} \right) - 3abc = 0\)
\( = > {a^3} + {b^3} + {c^3} + 3ab\left( {a + b + c} \right) + 3bc\left( {a + b + c} \right) + 3ac\left( {a + b + c} \right) = 3abc\)
\(Do{\rm{ }}a + b + c = 0\)
\( = > {a^3} + {b^3} + {c^3} = 3abc\) (đpcm).