Đề thi giữa kì 1 Toán 8 - Đề số 3 - Kết nối tri thức
Câu 1: Cho các biểu thức ({x^2} - 2 + 4x{y^2};frac{x}{y} + 2{y^2};2023;x(x - y)). Có bao nhiêu đa thức trong các biểu thức trên?
Đề bài
Phần trắc nghiệm ( 3 điểm)
Câu 1: Cho các biểu thức \({x^2} - 2 + 4x{y^2};\frac{x}{y} + 2{y^2};2023;x(x - y)\). Có bao nhiêu đa thức trong các biểu thức trên?
A. 1.
B. 2.
C. 3.
D. 4.
Câu 2: Thu gọn đa thức \( - 2{x^2}y - 7x{y^2} + 3{x^2}y + 7x{y^2}\) ta được
A. \(P = {x^2}y\).
B. \(P = - {x^2}y\).
C. \(P = {x^2}y + 14x{y^2}\).
D. \( - 5{x^2}y - 14x{y^2}\).
Câu 3: Bậc của đa thức \(4{x^2}y - {x^4} + 5x{y^2} + 3xy + {x^4}\)
A. 3.
B. 4.
C. 5.
D. 6.
Câu 4: Biểu thức (4x + y).(4x – y) bằng
A. \(16{x^2} - {y^2}\).
B. \( - 16{x^2} + {y^2}\).
C. \(16{x^2} + 4xy + {y^2}\).
D. \(16{x^2} - 8xy + {y^2}\).
Câu 5: Biểu thức \((4x + y)\left( {16{x^2} - 4xy + {y^2}} \right)\) bằng
A. \(64{x^3} + {y^3}\).
B. \(64{x^3} - {y^3}\).
C. \(64{x^3} - 9{x^2}y + {y^3}\).
D. \(64{x^3} - 9x{y^2} + {y^3}\).
Câu 6: Giá trị nhỏ nhất của biểu thức \(A = {(x - 15)^2} + 2023\) là
A. 15.
B. 2023.
C. 2248.
D. 2006.
Câu 7: Có bao nhiêu số nguyên dương m biết đa thức \(A = 8{x^2}{y^3} + 6{x^3}{y^2}\) chia hết cho \(B = 2{x^2}{y^m}\)
A. 0.
B. 1.
C. 2.
D. 3.
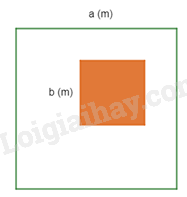
Câu 8: Giữa một cái sân hình vuông cạnh a mét, người ta xây một bồn hoa hình vuông có cạnh b mét (a > b). Đa thức S biểu thị diện tích còn lại của cái sân là
A. 4a – 4b.
B. a 2 – b 2 .
C. (a – b) 2 .
D. b 2 .
Câu 9 : Cho hình bình hành ABCD biết AB = 6cm, BC = 4cm. Khi đó chu vi của hình bình hành ABCD là
A. 10cm.
B. 20cm.
C. 24cm.
D. 48cm.
Câu 10 : Chọn câu sai trong các câu sau: Tứ giác có thể có:
A. 3 góc tù, 1 góc nhọn.
B. 3 góc vuông, 1 góc nhọn.
C. 2 góc tù, 2 góc nhọn.
D. 3 góc nhọn, 1 góc tù
Câu 11 : Một hình thang vuông có một góc bằng 75 0 , các góc còn lại của hình thang đó là:
A. 105 0 ; 105 0 ; 75 0 .
B. 90 0 ; 105 0 ; 75 0 .
C. 105 0 ; 75 0 ; 75 0 .
D. 105 0 ; 90 0 ; 90 0 .
Câu 12 : Chọn câu đúng nhất
A. Hình thang cân là hình thang có hai góc kề một đáy bằng nhau.
B. Trong hình thang cân, hai cạnh bên bằng nhau.
C. Trong hình thang cân, hai đường chéo bằng nhau.
D. Cả A, B, C đều đúng.
Phần tự luận ( 7 điểm)
Bài 1. ( 2 điểm) Cho đa thức
\(M = {x^2}y - \frac{1}{3}y - \frac{2}{3}{x^2}y{z^5} + 8{x^2}y + \frac{2}{3}{x^2}y{z^5}.\).
a) Thu gọn đa thức M.
b) Tìm bậc của đa thức M.
c) Tính giá trị của M khi x = 1; y = 3; z = 2023
Bài 2. ( 1,5 điểm)
1) Tìm x, biết:
a) \(3x(12x - 4) - 9x(4x - 3) = 30\);
b) \(3(x + 4) - {x^2} - 8x - 16 = 0\)
2) Bà Khanh dự định mua x hộp sữa (mỗi hộp giá 21 nghìn đồng) và y hộp kẹo (mỗi hộp giá 32 nghìn đồng). Nhưng khi đến cửa hàng, bà Khanh thấy giá sữa đã giảm 2 nghìn đồng mỗi hộp (giá kẹo như cũ) nên quyết định mua thêm 3 hộp sữa và bớt đi 1 hộp kẹo. Viết biểu thức biểu thị số tiền bà Khanh phải trả cho cửa hàng.
Bài 3. (3 điểm) Cho hình bình hành ABCD có E, F theo thứ tự là trung điểm của AB, CD.
a) Tứ giác DEBF là hình gì? Vì sao?
b) Chứng minh rằng các đường thẳng AC, BD, EF đồng quy tại một điểm.
c) Gọi giao điểm của AC với DE và BF theo thứ tự là M và N. Chứng minh rằng M và N đối xứng nhau qua O.
Bài 4. (0,5 điểm) Cho a; b; c thoả mãn:
\({a^{2022}}\; + {b^{2022}}\; + {c^{2022}}\; = {a^{1011}}{b^{1011}}{\rm{ + }}{b^{1011}}{c^{1011}}{\rm{ + }}{c^{1011}}{a^{1011}}\)
Tính giá trị của biểu thức
\(A = {\left( {a-b} \right)^{2020}} + {\left( {b-c} \right)^{2021}} + {\left( {a - c} \right)^{2022}}\)
---- Hết ----
Lời giải
Phần trắc nghiệm ( 3 điểm)
|
1. C |
2. A |
3. A |
4. B |
5. A |
6. B |
|
7. C |
8. D |
9. C |
10. B |
11. D |
12. D |
Câu 1: Cho các biểu thức \({x^2} - 2 + 4x{y^2};\frac{x}{y} + 2{y^2};2023;x(x - y)\). Có bao nhiêu đa thức trong các biểu thức trên?
|
A. 1. |
B. 2. |
|
C. 3. |
D. 4. |
Phương pháp
Dựa vào khái niệm đa thức: Đa thức là tổng của những đơn thức; mỗi đơn thức trong tổng gọi là một hạng tử của đa thức đó.
Lời giải
\({x^2} - 2 + 4x{y^2}\); \(2023;x(x - y)\) là những đa thức vì là tổng của những đơn thức.
\(\frac{x}{y} + 2{y^2}\) không phải đa thức vì \(\frac{x}{y}\) không phải là đơn thức.
Đáp án C.
Câu 2: Thu gọn đa thức \( - 2{x^2}y - 7x{y^2} + 3{x^2}y + 7x{y^2}\) ta được
|
A. \(P = {x^2}y\). |
B. \(P = - {x^2}y\). |
|
C. \(P = {x^2}y + 14x{y^2}\). |
D. \( - 5{x^2}y - 14x{y^2}\). |
Phương pháp
Cộng, trừ các hạng tử đồng dạng để rút gọn.
Lời giải
\(\begin{array}{l}P = - 2{x^2}y - 7x{y^2} + 3{x^2}y + 7x{y^2}\\ = \left( { - 2{x^2}y + 3{x^2}y} \right) + \left( { - 7x{y^2} + 7x{y^2}} \right)\\ = {x^2}y\end{array}\)
Đáp án A .
Câu 3: Bậc của đa thức \(4{x^2}y - {x^4} + 5x{y^2} + 3xy + {x^4}\)
|
A. 3. |
B. 4. |
|
C. 5. |
D. 6. |
Phương pháp
Sử dụng công thức \({A^2} - {B^2} = \left( {A - B} \right)\left( {A + B} \right)\).
Lời giải
\(\begin{array}{l}4{x^2}y - {x^4} + 5x{y^2} + 3xy + {x^4}\\ = 4{x^2}y + 5x{y^2} + 3xy + \left( { - {x^4} + {x^4}} \right)\\ = 4{x^2}y + 5x{y^2} + 3xy\end{array}\)
Đa thức có 3 hạng tử: \(4{x^2}y;5x{y^2};3xy\).
Hạng tử \(4{x^2}y\) có bậc là 2 + 1 = 3.
Hạng tử \(5x{y^2}\) có bậc là 1 + 2 = 3.
Hạng tử \(3xy\) có bậc là 1 + 1 = 2.
Vì bậc cao nhất của các hạng tử trong đa thức là 3 nên bậc của đa thức là 3.
Đáp án A .
Câu 4: Biểu thức (4x + y).(4x – y) bằng
|
A. \( - 16{x^2} + {y^2}\). |
B. \(16{x^2} - {y^2}\). |
|
C. \(16{x^2} + 4xy + {y^2}\). |
D. \(16{x^2} - 8xy + {y^2}\). |
Phương pháp
Dựa vào kiến thức của những hằng đẳng thức đáng nhớ.
Lời giải
\(\left( {4x + y} \right)\left( {4x - y} \right) = 16{x^2} - {y^2}\).
Đáp án B .
Câu 5: Biểu thức \((4x + y)\left( {16{x^2} - 4xy + {y^2}} \right)\) bằng
|
A. \(64{x^3} + {y^3}\). |
B. \(64{x^3} - {y^3}\). |
|
C. \(64{x^3} - 9{x^2}y + {y^3}\). |
D. \(64{x^3} - 9x{y^2} + {y^3}\). |
Phương pháp
Dựa vào kiến thức của những hằng đẳng thức đáng nhớ.
Lời giải
\((4x + y)\left( {16{x^2} - 4xy + {y^2}} \right) = {\left( {4x} \right)^3} + {y^3} = 64{x^3} + {y^3}\).
Đáp án A .
Câu 6: Giá trị nhỏ nhất của biểu thức \(A = {(x - 15)^2} + 2023\) là
|
A. 15. |
B. 2023. |
|
C. 2248. |
D. 2006. |
Phương pháp
Dựa vào đặc điểm của bậc chẵn.
Lời giải
Vì \({(x - 15)^2} \ge 0\) với mọi \(x \in \mathbb{R}\) nên \(A = {(x - 15)^2} + 2023 \ge 2023\) với mọi \(x \in \mathbb{R}\).
Vậy giá trị nhỏ nhất của biểu thức A là 2023.
Đáp án B .
Câu 7: Có bao nhiêu số nguyên dương m biết đa thức \(A = 8{x^2}{y^3} + 6{x^3}{y^2}\) chia hết cho \(B = 2{x^2}{y^m}\)
|
A. 0. |
B. 1. |
|
C. 2. |
D. 3. |
Phương pháp
Dựa vào quy tắc chia hết của đa thức cho đơn thức.
Lời giải
Để đa thức A chia hết cho đơn thức B thì mọi biến của đa thức A phải có bậc lớn hơn hoặc bằng bậc của các biến trong đơn thức B.
Biến y trong đa thức A có bậc nhỏ nhất là 2, vì vậy bậc của biến y trong B phải nhỏ hơn hoặc bằng 2. Bậc của biến y trong B có thể là hai giá trị: 1 hoặc 2. (0 không phải số nguyên dương).
Đáp án C .
Câu 8: Giữa một cái sân hình vuông cạnh a mét, người ta xây một bồn hoa hình vuông có cạnh b mét (a > b). Đa thức S biểu thị diện tích còn lại của cái sân là

|
A. 4a – 4b. |
B. b 2 . |
|
C. (a – b) 2 . |
D. a 2 – b 2 . |
Phương pháp
Dựa vào công thức tính diện tích hình vuông để viết đa thức.
Lời giải
Đơn thức biểu diễn diện tích cái sân là: a.a = a 2 .
Đơn thức biểu diễn diện tích bồn hoa là: b.b = b 2 .
Đa thức S biểu thị diện tích còn lại của cái sân là: S = a 2 – b 2 .
Đáp án D .
Câu 9: Cho hình bình hành ABCD biết AB = 6cm, BC = 4cm. Khi đó chu vi của hình bình hành ABCD là
|
A. 10cm. |
B. 24cm. |
|
C. 20cm. |
D. 48cm. |
Phương pháp
Dựa vào đặc điểm về cạnh của hình bình hành.
Lời giải
Vì hình bình hành ABCD có AB = CD; BC = AD nên chu vi hình bình hành ABCD là: 6.2 + 4.2 = 20 (cm).
Đáp án C .
Câu 10: Chọn câu sai trong các câu sau: Tứ giác có thể có:
A. 3 góc tù, 1 góc nhọn.
B. 3 góc vuông, 1 góc nhọn.
C. 2 góc tù, 2 góc nhọn.
D. 3 góc nhọn, 1 góc tù
Phương pháp
Dựa vào định lí tổng các góc của một tứ giác bằng 360 0 .
Lời giải
Nếu tứ giác có 3 góc vuông, 1 góc nhọn thì tổng 3 góc vuông là 3.90 0 = 270 => Góc còn lại phải bằng 360 0 – 270 0 = 90 0 > góc nhọn nên đáp án B sai.
Đáp án B .
Câu 11: Một hình thang vuông có một góc bằng 75 0 , các góc còn lại của hình thang đó là:
|
A. 105 0 ; 105 0 ; 75 0 . |
B. 90 0 ; 105 0 ; 75 0 . |
|
C. 105 0 ; 75 0 ; 75 0 . |
D. 105 0 ; 90 0 ; 90 0 . |
Phương pháp
Dựa vào định lí tổng các góc của một tứ giác bằng 360 0 .
Lời giải
Vì hình thang là hình thang vuông nên có hai góc bằng 90 0 và có một góc bằng 75 0 nên góc còn lại bằng:
\({360^0} - {90^0} - {90^0} - {75^0} = {105^0}\).
Đáp án D .
Câu 12: Chọn câu đúng nhất
A. Hình thang cân là hình thang có hai góc kề một đáy bằng nhau.
B. Trong hình thang cân, hai cạnh bên bằng nhau.
C. Trong hình thang cân, hai đường chéo bằng nhau.
D. Cả A, B, C đều đúng.
Phương pháp
Dựa vào tính chất của hình thang cân.
Lời giải
Các phương án A, B, C đều là các tính chất của hình thang cân nên đáp án đúng nhất là đáp án D.
Đáp án D.
Phần tự luận. (7 điểm)
Bài 1. ( 2 điểm) Cho đa thức
\(M = {x^2}y - \frac{1}{3}y - \frac{2}{3}{x^2}y{z^5} + 8{x^2}y + \frac{2}{3}{x^2}y{z^5}.\).
a) Thu gọn đa thức M.
b) Tìm bậc của đa thức M.
c) Tính giá trị của M khi x = 1; y = 3; z = 2023
Phương pháp
a) Sử dụng các quy tắc tính của đa thức để rút gọn đa thức.
b) Sử dụng kiến thức bậc của đa thức để tìm bậc của M.
c) Thay x, y, z vào để tính giá trị.
Lời giải
a) Thu gọn:
\(\begin{array}{l}M = {x^2}y - \frac{1}{3}y - \frac{2}{3}{x^2}y{z^5} + 8{x^2}y + \frac{2}{3}{x^2}y{z^5}\\ = {x^2}y + 8{x^2}y - \frac{1}{3}y - \frac{2}{3}{x^2}y{z^5} + \frac{2}{3}{x^2}y{z^5}\\ = ({x^2}y + 8{x^2}y) - \frac{1}{3}y - \left( {\frac{2}{3}{x^2}y{z^5} - \frac{2}{3}{x^2}y{z^5}} \right)\\ = 9{x^2}y - \frac{1}{3}y - 0\\ = 9{x^2}y - \frac{1}{3}y\end{array}\)
Vậy \(M = 9{x^2}y - \frac{1}{3}y.\)
b) Đa thức M có hai hạng tử: 9x 2 y và \( - \frac{1}{3}\)y.
+ Hạng tử 9x 2 y có bậc là 2 + 1 = 3.
+ Hạng tử \( - \frac{1}{3}\)y có bậc là 1.
Vì 3 > 1 nên bậc của đa thức M là 3.
c) Thay x = 1; y = 3; z = 2023 thì \(M = {9.1^2}.3 - \frac{1}{3}.3 = 27 - 1 = 26\).
Bài 2. ( 1,5 điểm)
1) Tìm x, biết:
a) \(3x(12x - 4) - 9x(4x - 3) = 30\);
b) \(3(x + 4) - {x^2} - 8x - 16 = 0\)
2) Bà Khanh dự định mua x hộp sữa (mỗi hộp giá 21 nghìn đồng) và y hộp kẹo (mỗi hộp giá 32 nghìn đồng). Nhưng khi đến cửa hàng, bà Khanh thấy giá sữa đã giảm 2 nghìn đồng mỗi hộp (giá kẹo như cũ) nên quyết định mua thêm 3 hộp sữa và bớt đi 1 hộp kẹo. Viết biểu thức biểu thị số tiền bà Khanh phải trả cho cửa hàng.
Phương pháp
1) Phân tích đa thức thành nhân tử để tìm x.
2) Dựa vào kiến thức của đa thức để tính số tiền bà Khanh phải trả cho cửa hàng.
Lời giải
1)
a)
\(\begin{array}{l}3x(12x - 4) - 9x(4x - 3) = 30\\36{x^2} - 12x - 36{x^2} + 27x = 30\\ - 12x + 27x = 30\\15x = 30\\x = 2\end{array}\)
Vậy x = 2.
b) \(3(x + 4) - {x^2} - 8x - 16 = 0\)
\(\begin{array}{l}3(x + 4) - \left( {{x^2} + 8x + 16} \right) = 0\\3(x + 4) - {\left( {x + 4} \right)^2} = 0\\\left( {x + 4} \right)\left( {3 - x - 4} \right) = 0\\\left( {x + 4} \right)\left( { - 1 - x} \right) = 0\\\left[ \begin{array}{l}x + 4 = 0\\ - 1 - x = 0\end{array} \right.\\\left[ \begin{array}{l}x = - 4\\x = - 1\end{array} \right.\end{array}\)
Vậy x = -4 hoặc x = -1.
2) Sữa giảm 2 nghìn đồng mỗi hộp nên giá mỗi hộp sữa tại cửa hàng là 21 – 2 = 19 (nghìn đồng).
Giá kẹo như cũ nên giá mỗi hộp kẹo tại cửa hàng vẫn là 32 nghìn đồng.
Tại cửa hàng, bà Khanh quyết định mua thêm 3 hộp sữa và bớt đi 1 hộp kẹo. Vậy bà Khanh đã mua x + 3 hộp sữa và y − 1 hộp kẹo.
Vậy số tiền bà Khanh phải trả cho cửa hàng là (x + 3).19 + (y − 1).32 (nghìn đồng).
Thu gọn biểu thức trên: \(\left( {x + 3} \right).19 + \left( {y - 1} \right).32\)
\(\begin{array}{l} = 19x + 3.19 + 32y - 32 = 19x + 57 + 32y - 32\\ = 19x + 32y + 25\end{array}\)
Vậy biểu thức biểu thị số tiền bà Khanh phải trả cho cửa hàng là \(19x + 32y + 25\) (nghìn đồng).
Bài 3. (2,5 điểm) ) Cho hình bình hành ABCD có E, F theo thứ tự là trung điểm của AB, CD.
a) Tứ giác DEBF là hình gì? Vì sao?
b) Chứng minh rằng các đường thẳng AC, BD, EF đồng quy tại một điểm.
c) Gọi giao điểm của AC với DE và BF theo thứ tự là M và N. Chứng minh rằng M và N đối xứng nhau qua O.
Phương pháp
a) Chứng minh tứ giác DEBF có một cặp cạnh đối song song và bằng nhau nên là hình bình hành.
b) Chứng minh giao điểm của AC với BC và giao điểm của BD với EF trùng nhau.
c) - Chứng minh M là trọng tâm của \(\Delta ABD\) \( \Rightarrow OM = \frac{1}{3}OA\)
- Chứng minh N là trọng tâm của \(\Delta BCD\) \( \Rightarrow ON = \frac{1}{3}OC\)
- Mà \(OA = OC \Rightarrow OM = ON\)
Lời giải
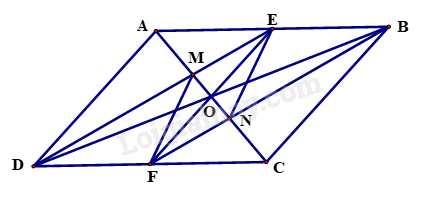
a) Vì ABCD là hình bình hành nên AB // CD, AB = CD.
Vì E, F là trung điểm của AB, CD nên AE = EB = CF = FD (vì AB = CD).
Xét tứ giác DEBF có:
EB // DF (vì AB // CD)
EB = DF (cmt)
=> DEBF là hình bình hành (tứ giác có cặp cạnh đối song song và bằng nhau).
b) Vì ABCD là hình bình hành nên AC và BD cắt nhau tại trung điểm của mỗi đường. Gọi O là giao điểm của AC và BD, khi đó O là trung điểm của AC, O là trung điểm của BD. (1)
Vì DEBF là hình bình hành nên BD và EF cắt nhau tại trung điểm của mỗi đường. Vì O là trung điểm của BD nên O cùng là trung điểm của EF. Khi đó BD và EF cắt nhau tại O. (2)
Từ (1) và (2) suy ra AC, BD, EF đồng quy tại điểm O.
c) Xét tam giác ABD có:
DE là đường trung tuyến của tam giác ABD (vì E là trung điểm của AB)
AO là đường trung tuyến của tam giác ABD (vì O là trung điểm của BD)
DE cắt AO tại M (vì giao điểm của AC và DE là M)
Suy ra M là trọng tâm của tam giác ABD nên AM = \(\frac{2}{3}\)AO và OM = \(\frac{1}{3}\)AO.
Tương tự, ta chứng minh được N là trọng tâm của tam giác BCD nên CN = \(\frac{2}{3}\)OC và ON = \(\frac{1}{3}\)OC.
Mà AO = OC (vì O là trung điểm của AC).
=> OM = ON.
Bài 4. (0,5 điểm) Cho a; b; c thoả mãn:
\({a^{2022}}\; + {b^{2022}}\; + {c^{2022}}\; = {a^{1011}}{b^{1011}}{\rm{ + }}{b^{1011}}{c^{1011}}{\rm{ + }}{c^{1011}}{a^{1011}}\)
Tính giá trị của biểu thức
\( \Rightarrow 2\left( {{a^{2022}}\; + {b^{2022}}\; + {c^{2022}}\;} \right) = 2\left( {{a^{1011}}{b^{1011}}{\rm{ + }}{b^{1011}}{c^{1011}}{\rm{ + }}{c^{1011}}{a^{1011}}} \right)\)
Phương pháp
Dựa vào hằng đẳng thức \({a^2} - {b^2} = \left( {a - b} \right)\left( {a + b} \right)\) để chứng minh.
Lời giải
Ta có: \({a^{2022}}\; + {b^{2022}}\; + {c^{2022}}\; = {a^{1011}}{b^{1011}}{\rm{ + }}{b^{1011}}{c^{1011}}{\rm{ + }}{c^{1011}}{a^{1011}}\)
\( \Rightarrow 2\left( {{a^{2022}}\; + {b^{2022}}\; + {c^{2022}}\;} \right) = 2\left( {{a^{1011}}{b^{1011}}{\rm{ + }}{b^{1011}}{c^{1011}}{\rm{ + }}{c^{1011}}{a^{1011}}} \right)\)
\(\left( {{a^{2022}} - 2{a^{1011}}{b^{1011}} + {b^{2022}}} \right) + \left( {{b^{2022}} - 2{b^{1011}}{c^{1011}} + {c^{2022}}} \right) + \left( {{c^{2022}} - 2{c^{1011}}{a^{1011}} + {a^{2022}}} \right) = 0\)
\( \Rightarrow {\left( {{a^{1011}} - {b^{1011}}} \right)^2} + {\left( {{b^{1011}} - {c^{1011}}} \right)^2} + {\left( {{c^{1011}} - {a^{1011}}} \right)^2} = 0\)
Vì \({x^2} \ge 0\) với \(\forall x\) nên dấu “=” xảy ra khi và chỉ khi
\({a^{1011}} - {b^{1011}} = {b^{1011}} - {c^{1011}} = {c^{1011}} - {a^{1011}} = 0 \Leftrightarrow a = b = c\)
\( \Rightarrow \) \(A = {\left( {a-b} \right)^{2020}} + {\left( {b-c} \right)^{2021}} + {\left( {a - c} \right)^{2022}} = 0\)