Đề thi học kì 1 Toán 10 Chân trời sáng tạo - Đề số 1 — Không quảng cáo

Đề bài

I. Phần trắc nghiệm (6 điểm – 30 câu)

Câu 1: Trong các mệnh đề sau, mệnh đề nào đúng?

A. $\forall x \in \mathbb{R},\,x \le {x^2}$ B. $\forall x \in \mathbb{R},\,\,\left| x \right| < 3 \Leftrightarrow x < 3$

C. $\forall n \in \mathbb{N},\,\,{n^2} + 1$chia hết cho 3 D. $\exists a \in \mathbb{Q},\,{a^2} = 2$

Câu 2: Cho mệnh đề “$\forall x \in \mathbb{R},{x^2} - x + 2023 < 0$”. Mệnh đề nào sau đây là mệnh đề phủ định của mệnh đề đã cho?

A. $\forall x \in \mathbb{R},{x^2} - x + 2023 \ge 0$ B. $\exists x \in \mathbb{R},{x^2} - x + 2023 < 0$

C. $\exists x \in \mathbb{R},{x^2} - x + 2023 \ge 0$ D. $\forall x \in \mathbb{R},{x^2} - x + 2023 > 0$

Câu 3: Cho $A = \left\{ {1,2,3} \right\}$.Trong các khẳng định sau, khẳng định nào sai:

A. $\emptyset  \subset A$ B. $1 \in A$ C. $\left\{ {1,2} \right\} \subset A$ D. $\left\{ 3 \right\} \in A$

Câu 4: Các phần tử của tập hợp $A = \left\{ {x \in \mathbb{R}:2{x^2} - 5x + 3 = 0} \right\}$là

A. $A = \left\{ 0 \right\}$ B. $A = \left\{ 1 \right\}$ C. $A = \left\{ {\frac{3}{2}} \right\}$ D. $A = \left\{ {1;\frac{3}{2}} \right\}$

Câu 5: Cho tập hợp $A = \left\{ { - 2,1,2,3,4} \right\}$, $B = \left\{ {x \in \mathbb{N}:{x^2} - 4 = 0} \right\}$. Mệnh đề nào sau đây là đúng?

A. $A \cap B = \left\{ 2 \right\}$ B. $A \cap B = \left\{ { - 2,2} \right\}$ C. $A \cup B = B$ D. $A\backslash B = \left\{ {1,3,4} \right\}$

Câu 6: Biểu diễn trên trục số các tập hợp $\left[ { - 4,3} \right]\backslash \left[ { - 2,1} \right]$ là hình nào dưới đây.

A.

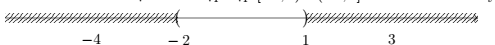
B.

C.

D.

Câu 7: Miền nghiệm của bất phương trình $x + 2y < 4$ là nửa mặt phẳng không chứa điểm nào trong các điểm sau?

A. $\left( {0;0} \right)$ B. $\left( {0;0} \right)$ C. $\left( {4;2} \right)$ D. $\left( {1; - 1} \right)$

Câu 8: Điểm nào sau đây thuộc miền nghiệm của hệ bất phương trình $\left\{ {\begin{array}{*{20}{c}}{2x - 5y - 1 > 0}\\{2x + y + 5 > 0}\\{x + y + 1 < 0}\end{array}} \right.$?

A. $\left( {0;0} \right)$ B. $\left( {1;0} \right)$ C. $\left( {0; - 2} \right)$ D. $\left( {0;2} \right)$

Câu 9: Để điều tra các con trong mỗi gia đình của một chung cư gồm 100 gia đình . Người ta chọn ra 20 gia đình ở tầng 4 và thu được mẫu số liệu sau đây :  2  4  2  1  3  5  1  1  2  3 1  2  2  3  4  1  1  2  3  4. Kích thước mẫu là bao nhiêu?

A. 5 B. 20 C. 4 D. 100

Câu 10: Thống kê điểm thi môn toán trong một kỳ thi của 400 HS. Người ta thấy có 80 bài được điểm 7. Hỏi tần suất của giá trị ${x_i} = 7$là bao nhiêu?

A. 80% B. 36% C. 20% D. 10%

Câu 11: Cho bảng số liệu ghi lại điểm của 40 học sinh trong bài kiểm tra 1 tiết môn toán

Số trung bình là?

A. 6,1 B. 6,5 C. 6,7 D. 6,9

Câu 12: Chọn câu đúng trong bốn phương án trả lời đúng sau đây. Độ lệch chuẩn là :

A. Bình phương của phương sai B. Một nửa của phương sai

C. Căn bậc hai của phương sai D. Không phải là các công thức trên.

Câu 13: 100 học sinh tham dự kì thi học sinh giỏi toán ( thang điểm là 20 ) . Kết quả cho trong bảng sau:

Điểm (x)	9	10	11	12	13	14	15	16	17	18	19
Tần số (n )	1	1	3	5	8	13	19	24	14	10	2

Số trung vị của bảng trên là :

A. 14,23 B. 15,28 C. 15,50 D. 16,50

Câu 14: 100 học sinh tham dự kì thi học sinh giỏi toán (thang điểm là 20) . Kết quả cho trong bảng sau:

Điểm (x)	9	10	11	12	13	14	15	16	17	18	19
Tần số (n )	1	1	3	5	8	13	19	24	14	10	2

Phương sai là:

A. 17,7 B. 15 C. 16 D. 15,50

Câu 15: Tìm tập xác định D của hàm số $y = \frac{{3x - 1}}{{2x - 2}}$.

A. $D = \mathbb{R}$ B. $D = \left( {1; + \infty } \right)$ C. $D = \mathbb{R}\backslash \left\{ 1 \right\}$ D. $D = \left[ {1; + \infty } \right)$

Câu 16: Tìm tập xác định ${\rm{D}}$ của hàm số $y = \frac{{\sqrt {2 - x}  + \sqrt {x + 2} }}{x}.$

A. ${\rm{D}} = \left[ { - 2;2} \right].$ B. ${\rm{D}} = \left( { - 2;2} \right)\backslash \left\{ 0 \right\}.$ C. ${\rm{D}} = \left[ { - 2;2} \right]\backslash \left\{ 0 \right\}.$ D. ${\rm{D}} = \mathbb{R}.$

Câu 17: Cho hàm số $y = f\left( x \right) = \left| { - 5x} \right|$. Khẳng định nào sau đây là sai?

A. $f\left( { - 1} \right) = 5$ B. $f\left( 2 \right) = 10$ C. $f\left( { - 2} \right) = 10$ D. $f\left( {\frac{1}{5}} \right) = {\rm{ \;}} - 1$

Câu 18: Điểm nào sau đây thuộc đồ thị hàm số $y = \frac{{\sqrt {{x^2} - 4x + 4} }}{x}$.

A. $A\left( {2;0} \right)$ B. $B\left( {3;3} \right)$ C. $C\left( {1; - 1} \right)$ D. $D\left( { - 1;3} \right)$

Câu 19: Giá trị nhỏ nhất của hàm số $y = x - 2\sqrt {x + 2}$ là:

A. – 4 B. – 3 C. – 2 D. - 1

Câu 20: Cho hàm số $y = 2{x^2} + 6x + 3$ có đồ thị (P). Trục đối xứng của (P) là:

A. $x = \frac{{ - 3}}{2}$ B. $x = \frac{{ - 2}}{3}$ C. $x = 2$ D. $x =  - 2$

Câu 21: Giá trị của $\cos {60^{\rm{o}}} + \sin {30^{\rm{o}}}$ bằng bao nhiêu?

A. $\frac{{\sqrt 3 }}{2}$ B. $\sqrt 3$ C. $\frac{{\sqrt 3 }}{3}$ D. $1$

Câu 22: Tam giác $ABC$ có $a = 8,c = 3,\widehat B = {60^0}.$ Độ dài cạnh $b$ bằng bao nhiêu?

A. $49.$ B. $\sqrt {97}$ C. $7.$ D. $\sqrt {61} .$

Câu 23: Cho tam giác ABC có ${a^2} = {b^2} + {c^2} - bc$. Số đo góc A là

A. 30 B. 60 C. 45 D. 90

Câu 24: Cho tam giác $ABC$ có góc $\widehat {BAC} = 60^\circ$ và cạnh $BC = \sqrt 3$. Tính bán kính của đường

tròn ngoại tiếp tam giác $ABC$.

A. $R = 4$ B. $R = 1$ C. $R = 2$ D. $R = 3$

Câu 25: Chọn phát biểu sai:

A. Ba điểm phân biệt A, B, C thẳng hàng khi và chỉ khi $\overrightarrow {AB}  = k\overrightarrow {BC} ,\,k \ne 0$

B. Ba điểm phân biệt A, B, C thẳng hàng khi và chỉ khi $\overrightarrow {AC}  = k\overrightarrow {BC} ,\,k \ne 0$

C. Ba điểm phân biệt A, B, C thẳng hàng khi và chỉ khi $\overrightarrow {AB}  = k\overrightarrow {AC} ,\,k \ne 0$

D. Ba điểm phân biệt A, B, C thẳng hàng khi và chỉ khi $\overrightarrow {AB}  = k\overrightarrow {AC}$

Câu 26: Tính tổng $\overrightarrow {MN}  + \overrightarrow {PQ}  + \overrightarrow {RN}  + \overrightarrow {NP}  + \overrightarrow {QR}$

A. $\overrightarrow {MR} .$ B. $\overrightarrow {MN} .$ C. $\overrightarrow {PR} .$ D. $\overrightarrow {MP} .$

Câu 27: Gọi $O$ là tâm hình bình hành $ABCD$. Đẳng thức nào sau đây sai?

A. $\overrightarrow {OA}  - \overrightarrow {OB}  = \overrightarrow {CD} .$ B. $\overrightarrow {OB}  - \overrightarrow {OC}  = \overrightarrow {OD}  - \overrightarrow {OA} .$

C. $\overrightarrow {AB}  - \overrightarrow {AD}  = \overrightarrow {DB} .$ D. $\overrightarrow {BC}  - \overrightarrow {BA}  = \overrightarrow {DC}  - \overrightarrow {DA} .$

Câu 28: Nếu G là trọng tâm tam giác ABC thì đẳng thức nào sau đây đúng.

A. $\overrightarrow {AG}  = \frac{3}{2}\left( {\overrightarrow {AB}  + \overrightarrow {AC} } \right)$ B. $\overrightarrow {AG}  = \frac{1}{3}\left( {\overrightarrow {AB}  + \overrightarrow {AC} } \right)$ C. $\overrightarrow {AG}  = \frac{2}{3}\left( {\overrightarrow {AB}  + \overrightarrow {AC} } \right)$ D. $\overrightarrow {AG}  = \frac{1}{3}\left( {\overrightarrow {AB}  + \overrightarrow {AC} } \right)$

Câu 29: Cho tam giác ABC đều cạnh 4 cm. Giá trị của tích vô hướng $\overrightarrow {AB} .\overrightarrow {BC} .$

A. 8 B. – 8 C. 4 D. - 4

Câu 30: Cho tam giác ABC. $H$ là trung điểm của $BC$. Tính $\left| {\overrightarrow {CA}  - \overrightarrow {HC} } \right|.$

A. $\left| {\overrightarrow {CA}  - \overrightarrow {HC} } \right| = \frac{a}{2}.$ B. $\left| {\overrightarrow {CA}  - \overrightarrow {HC} } \right| = \frac{{3a}}{2}.$ C. $\left| {\overrightarrow {CA}  - \overrightarrow {HC} } \right| = \frac{{2\sqrt 3 a}}{3}.$ D. $\left| {\overrightarrow {CA}  - \overrightarrow {HC} } \right| = \frac{{a\sqrt 7 }}{2}.$

II. Tự luận (4 điểm)

Câu 1: 592203) Lớp 10A có 40 học sinh trong đó có 10 bạn giỏi Toán, 15 bạn giỏi Lý, và 22 bạn không giỏi môn học nào trong hai môn Toán, Lý. Hỏi lớp 10A có bao nhiêu bạn học sinh vừa giỏi Toán, vừa giỏi Lý?

Câu 2: 592204) Cho hàm số bậc hai $y = a{x^2} + bx + c$ có f(0) = 1, f(1) = 4, f(2) = 5.

a. Hãy xác định các hệ số a, b, c.

b. Xác định tập giá trị, lập bảng biến thiên và vẽ đồ thị hàm số

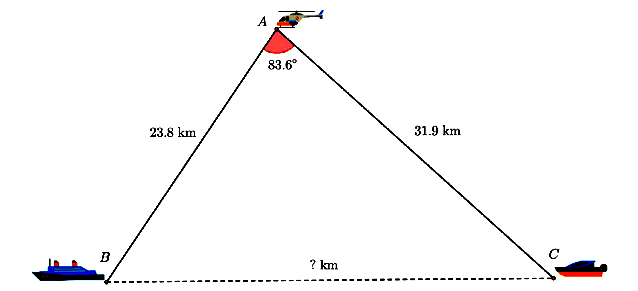
Câu 3: 592205) Một máy bay trực thăng A quan sát hai tàu B và C cách trực thăng 23,8 km và C cách trực thăng 31,9 km. Góc nhìn $\angle BAC$từ trực thăng đến hai thuyền là 83,6 độ. Hỏi hai chiếc tàu cách nhau bao xa và độ cao của máy bay so với mặt nước biển là bao nhiêu? Làm tròn kết quả đến hàng phần trăm.

Câu 4. 592206) Cho tam giác ABC có trung tuyến AM, BN, CP. Chứng minh

a. $\overrightarrow {AM}  + \overrightarrow {BN}  + \overrightarrow {CP}  = \overrightarrow 0$

b. $\overrightarrow {AP}  + \overrightarrow {BM}  = \frac{1}{2}\overrightarrow {AC}$

----- HẾT -----

Lời giải

HƯỚNG DẪN  CHI TIẾT

I. Phần trắc nghiệm (6 điểm – 30 câu)

Câu 1 (TH):

Phương pháp:

Mệnh đề chưa biến sai khi tìm được ít nhất 1 giá trị không thỏa mãn.

Cách giải:

Dùng phương pháp loại trừ

A sai khi $x = \frac{1}{2}$, B sai vì x = -4 không thỏa mãn, D sai do $a = \sqrt 2$không là số hữu tỉ

Chọn C.

Câu 2 (TH):

Phương pháp:

Phủ định của $\forall$ là $\exists$, phủ định của < là $\ge$

Cách giải:

Phủ định của  $\forall x \in \mathbb{R},{x^2} - x + 2023 < 0$ là $\exists x \in \mathbb{R},{x^2} - x + 2023 \ge 0$.

Chọn C.

Câu 3 (NB):

Phương pháp:

Kí hiệu $\in$ để chỉ phần tử thuộc tập hợp.

Kí hiệu $\subset$ để chỉ tập hợp là tập hợp con của 1 tập hợp.

Cách giải:

D sai do $\left\{ 3 \right\}$là 1 tập hợp nên ta không dùng kí hiệu $\in$.

Chọn D.

Câu 4 (TH):

Phương pháp:

phương trình $2{x^2} - 5x + 3 = 0$ và đối chiếu điều kiện của x

Cách giải:

$2{x^2} - 5x + 3 = 0 \Leftrightarrow \left[ \begin{array}{l}x = \frac{3}{2} \in \mathbb{R}\\x = 1 \in \mathbb{R}\end{array} \right. \Rightarrow A = \left\{ {1;\frac{3}{2}} \right\}$

Chọn D.

Câu 5 (TH):

Phương pháp:

Áp dụng định nghĩa tìm các phép toán trên tập hợp.

Cách giải:

$B = \left\{ {x \in \mathbb{N}:{x^2} - 4 = 0} \right\} = \left\{ 2 \right\} \Rightarrow A \cap B = \left\{ 2 \right\}$

Chọn A.

Câu 6 (TH): -

Phương pháp:

Biểu diễn các tập hợp trên trục số và áp dụng định nghĩa các phép toán trên tập hợp.

Cách giải:

Chọn B.

Câu 7 (NB):

Phương pháp:

Thay tọa độ các điểm vào bất phương trình và kiểm tra tính đúng sai.

Cách giải:

Vì 4 + 2.2=8 > 4 nên $\left( {4;2} \right)$ không thuộc miền nghiệm của bất phương trình $x + 2y < 4$.

Chọn C.

Câu 8 (TH):

Phương pháp:

Thay tọa độ các điểm vào bất phương trình và kiểm tra tính đúng sai

Cách giải:

Vì $\left( {0; - 2} \right)$thỏa mãn cả 3 phương trình nên $\left( {0; - 2} \right)$ thuộc miền nghiệm của hệ bất phương trình.

Chọn C.

Câu 9 (NB):

Phương pháp:

Kích thước mẫu là số phần tử của 1 mẫu số liệu

Cách giải:

Có tất cả 20 mẫu số liệu thống kê nên kích thước mẫu bằng 20.

Chọn B.

Câu 10 (TH):

Phương pháp:

Tần suất ${f_i}$của giá trị ${x_i}$ là tỉ số giữa tần số n và kích thước mẫu N có công thức ${f_i} = \frac{n}{N}$.

Cách giải:

${f_i} = \frac{{80}}{{400}} = 0,2 = 20\%$

Chọn C.

Câu 11 (TH):

Phương pháp:

Số trung bình là $\overline x  = \frac{{{x_1} + {x_2} + {x_3} + ... + {x_n}}}{n}$

Cách giải:

$\overline x  = \frac{{3.2 + 4.3 + 5.7 + 6.18 + 7.3 + 8.2 + 9.4 + 10.1}}{{40}} = 6,1$

Chọn A.

Câu 12 (TH):

Phương pháp:

Độ lệch chuẩn là căn bậc hai của phương sai

Cách giải:

Chọn C.

Câu 13 (TH):

Phương pháp:

Dùng MTCT để tính

Cách giải:

Chọn C.

Câu 14 (TH):

Phương pháp:

Dùng MTCT để tính

Cách giải:

Chọn C.

Câu 15 (NB):

Phương pháp:

Hàm phân thức xác định khi mẫu thức khác 0.

Cách giải:

ĐKXĐ: $2x - 2 \ne 0 \Leftrightarrow x \ne 1$.

Vậy TXĐ của hàm số là $D = \mathbb{R}\backslash \left\{ 1 \right\}$.

Chọn C.

Câu 16 (TH):

Phương pháp:

Căn bậc 2 xác định khi biểu thức trong căn không âm.

Cách giải:

TXĐ của hàm số: $\left\{ \begin{array}{l}2 - x \ge 0\\x + 2 \ge 0\\x \ne 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l} - 2 \le x \le 2\\x \ne 0\end{array} \right.$

Vậy TXĐ của hàm số là $D = \left[ { - 2;2} \right]\backslash \left\{ 0 \right\}$

Chọn A.

Câu 17 (NB):

Phương pháp:

Tính giá trị hàm số tại 1 điểm.

Cách giải:

$\begin{array}{*{20}{l}}{f\left( { - 1} \right) = \left| { - 5.\left( { - 1} \right)} \right| = 5}\\{f\left( 2 \right) = \left| { - 5.2} \right| = 10}\\{f\left( { - 2} \right) = \left| { - 5.\left( { - 2} \right)} \right| = 10}\\{f\left( {\frac{1}{5}} \right) = \left| { - 5.\frac{1}{5}} \right| = 1}\end{array}$

Vậy đáp án D sai.

Chọn D.

Câu 18 (TH):

Phương pháp:

Thay tọa độ các điểm ở các đáp án vào hàm số. Điểm nào thỏa mãn hàm số thì sẽ thuộc đồ thị hàm số.

Cách giải:

Thay tọa độ điểm $A\left( {2;0} \right)$ vào hàm số: $0 = \frac{{\sqrt {{2^2} - 4.2 + 4} }}{2}$ (đúng) nên A thuộc đồ thị hàm số.

Chọn A.

Câu 19 (VD):

Phương pháp:

Phân tích biêu thức về dạng có hằng đẳng thức

Cách giải:

$D = [ - 2; + \infty )$

$y = x - 2\sqrt {x + 2}  = x + 2 - 2\sqrt {x + 2}  + 1 - 1 = {\left( {\sqrt {x + 2}  - 1} \right)^2} - 1 \ge  - 1$ khi x = -1

Chọn D.

Câu 20 (NB):

Phương pháp:

Trục đối xứng của hàm số bậc hai $y = a{x^2} + bx + c$ là $x = \frac{{ - b}}{{2a}}$

Cách giải:

$y = 2{x^2} + 6x + 3$ có a = 2, b = 6, c = 3 nên trục đối xứng $x = \frac{{ - 6}}{{2.2}} = \frac{{ - 3}}{2}$

Chọn A.

Câu 21 (NB):

Phương pháp:

Dùng bảng các giá trị lượng giác đặc biệt.

Cách giải:

$\cos {60^{\rm{o}}} + \sin {30^{\rm{o}}} = \frac{1}{2} + \frac{1}{2} = 1$

Chọn D.

Câu 22 (NB):

Phương pháp:

Dùng định lý cosin ${b^2} = {a^2} + {c^2} - 2ac.\cos B$

Cách giải:

${b^2} = {a^2} + {c^2} - 2ac.\cos B = {8^2} + {3^2} - 2.3.8.\cos 60 = 49 \Rightarrow b = 7$

Chọn C.

Câu 23 (TH):

Phương pháp:

Dùng định lý cosin $\cos A = \frac{{{b^2} + {c^2} - {a^2}}}{{2bc}}$

Cách giải:

$\cos A = \frac{{{b^2} + {c^2} - {a^2}}}{{2bc}} = \frac{{{b^2} + {c^2} - \left( {{b^2} + {c^2} - bc} \right)}}{{2bc}} = \frac{1}{2} \Rightarrow \angle A = {60^0}$

Chọn B.

Phương pháp:

Dùng định lý sin:  $\frac{a}{{\sin A}} = \frac{b}{{\sin B}} = \frac{c}{{\sin C}} = 2R$

Cách giải:

$\frac{a}{{\sin A}} = 2R \Leftrightarrow \frac{{\sqrt 3 }}{{\sin 60}} = 2R \Rightarrow R = 1$

Chọn B.

Câu 25 (NB):

Phương pháp:

Dùng định lý về 3 điểm thẳng hàng.

Cách giải:

D sai do khi k = 0 thì $\overrightarrow {AB}  = \overrightarrow 0$

Chọn D.

Câu 26 (TH):

Phương pháp:

Dùng quy tắc cộng, trừ hai vecto

Cách giải:

$\begin{array}{l}\overrightarrow {MN}  + \overrightarrow {PQ}  + \overrightarrow {RN}  + \overrightarrow {NP}  + \overrightarrow {QR}  = \overrightarrow {MN}  + \overrightarrow {NP}  + \overrightarrow {PQ}  + \overrightarrow {QR}  + \overrightarrow {RN} \\\,\, = \overrightarrow {MP}  + \overrightarrow {PR}  + \overrightarrow {RN}  = \overrightarrow {MR}  + \overrightarrow {RN}  = \overrightarrow {MN} \end{array}$

Chọn B.

Câu 27 (VD):

Phương pháp:

Dùng quy tắc cộng, trừ hai vecto

Cách giải:

$\overrightarrow {OB}  - \overrightarrow {OC}  = \overrightarrow {CB} ,\,\,\overrightarrow {OD}  - \overrightarrow {OA}  = \overrightarrow {AD}$mà $\overrightarrow {CB} ,\,\,\overrightarrow {AD}$là 2 vecto ngược hướng nên B sai

Chọn B.

Câu 28 (VD):

Phương pháp:

Nếu M là trung điểm của AB thì với mọi điểm O là luôn có $\overrightarrow {OA}  + \overrightarrow {OB}  = 2\overrightarrow {OM}$

Cách giải:

Gọi M là trung điểm của AC khi đó $\overrightarrow {AB}  + \overrightarrow {AC}  = 2\overrightarrow {AM}$. Do G là trọng tâm tam giác ABC nên $\overrightarrow {AG}  = \frac{2}{3}\overrightarrow {AM}$. Suy ra $\overrightarrow {AG}  = \frac{2}{3}.\frac{1}{2}\left( {\overrightarrow {AB}  + \overrightarrow {AC} } \right) = \frac{1}{3}\left( {\overrightarrow {AB}  + \overrightarrow {AC} } \right)$

Chọn D.

Phương pháp:

$\overrightarrow a .\overrightarrow b  = \left| {\overrightarrow a } \right|.\left| {\overrightarrow b } \right|.\cos \left( {\overrightarrow a ,\,\overrightarrow b } \right)$

Cách giải:

$\overrightarrow {AB} .\overrightarrow {BC}  = \left| {\overrightarrow {AB} } \right|.\left| {\overrightarrow {BC} } \right|.\cos \left( {\overrightarrow {AB} ,\,\overrightarrow {BC} } \right) = 4.4.\cos 120 =  - 8$

Chọn B.

Câu 30 (VD):

Phương pháp:

Cách giải:

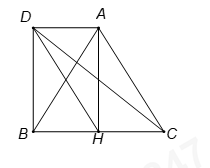
Gọi $D$ là điểm thỏa mãn tứ giác $ACHD$ là hình bình hành

$\Rightarrow AHBD$ là hình chữ nhật.

$\left| {\overrightarrow {CA}  - \overrightarrow {HC} } \right| = \left| {\overrightarrow {CA}  + \overrightarrow {CH} } \right| = \left| {\overrightarrow {CD} } \right| = CD.$

Ta có $CD = \sqrt {B{D^2} + B{C^2}}  = \sqrt {A{H^2} + B{C^2}}  = \sqrt {\frac{{3{a^2}}}{4} + {a^2}}  = \frac{{a\sqrt 7 }}{2}.$

Chọn D.

II. Phần tự luận (4 điểm)

Câu 1 (VD):

Phương pháp:

Dùng các phép toán trên tập hợp

Cách giải:

Gọi tập hợp các học sinh giỏi Toán là A. Khi đó n(A)=10

Gọi tập hợp các học sinh giỏi Lý là B. Khi đó n(B)=15

Số học sinh học giỏi toán hoặc giỏi lý là $n\left( {A \cup B} \right)$ là 40 – 22=18 học sinh

Vậy số học sinh giỏi cả 2 môn Toán Lý là $n\left( {A \cap B} \right) = n\left( A \right) + n\left( B \right) - n\left( {A \cup B} \right) = 10 + 15 - 18 = 7$

Vậy có tất cả 7 học sinh vừa giỏi Toán vừa giỏi Lý.

Câu 2 (VD):

Phương pháp:

Tính giá trị của hàm số tại các điểm cho trước, lập hệ phương trình tìm a, b, c.

Cách giải:

a. Từ f(0) = 1, f(1) = 4, f(2) = 5 ta có hệ phương trình

$\left\{ \begin{array}{l}a{.0^2} + b.0 + c = 1\\a{.1^2} + b.1 + c = 4\\a{.2^2} + b.2 + c = 5\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}c = 1\\a + b + 1 = 4\\4a + 2b + 1 = 5\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}c = 1\\a =  - 1\\b = 4\end{array} \right.$

Vậy hàm số có dạng $y =  - {x^2} + 4x + 1$

b. $y =  - {x^2} + 4x + 1$

Đỉnh S có tọa độ $x = \frac{{ - 4}}{{2.\left( { - 1} \right)}} = 2$, $y =  - {2^2} + 4.2 + 1 = 5$

Vì hàm số có a = -1 < 0 nên ta có bảng biến thiên

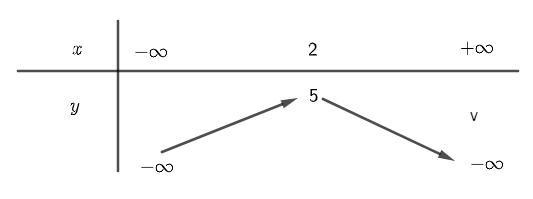
Vậy hàm số đạt giá trị lớn nhất bằng 5 khi x = 1.

Tập giá trị của hàm số là $( - \infty ,5]$

Đồ thị:

Trong mặt phẳng Oxy đồ thị của $y =  - {x^2} + 4x + 1$là parabol (P) có:

Đỉnh S (2,5)

Trục đối xứng là x = 2

Bề lõm quay xuống

Cắt trục tung tại điểm (0,1)

Câu 3 (TH):

Phương pháp:

Dùng các định cosin, công thức diện tích tỏng tam giác.

Cách giải:

Ta có $B{C^2} = A{B^2} + A{C^2} - 2AB.AC.\cos A = 23,{8^2} + 31,{9^2} - 2.23,8.31,9.\cos 83,6 = 1414,791$

Suy ra $BC \approx 37,61$km

Gọi khoảng cách từ máy bay A đến mặt nước biển là d. Khi đó áp dụng công thức diện tích tam giác ta có

$\begin{array}{l}S = \frac{1}{2}.AB.AC.\sin A = \frac{1}{2}.d.BC\\ \Leftrightarrow d = \frac{{AB.AC.\sin A}}{{BC}} = \frac{{23,8.31,9.\sin 83,6}}{{37,61}} \approx 20,06\end{array}$

Vậy khoảng cách giữa hai tàu BC là 37,61km và độ cao của máy bay A so với mặt nước biển là 20,06km.

Câu 4 (VD):

Phương pháp:

Nếu M là trung điểm của AB thì với mọi điểm O là luôn có $\overrightarrow {OA}  + \overrightarrow {OB}  = 2\overrightarrow {OM}$

Cách giải:

a. Ta có $\overrightarrow {AM}  = \frac{1}{2}\left( {\overrightarrow {AC}  + \overrightarrow {AB} } \right),\,\overrightarrow {BN}  = \frac{1}{2}\left( {\overrightarrow {BC}  + \overrightarrow {BA} } \right),\,\overrightarrow {CP}  = \frac{1}{2}\left( {\overrightarrow {CA}  + \overrightarrow {CB} } \right)$ nên

$\begin{array}{l}\overrightarrow {AM}  + \overrightarrow {BN}  + \overrightarrow {CP}  = \frac{1}{2}\left( {\overrightarrow {AC}  + \overrightarrow {AB} } \right) + \frac{1}{2}\left( {\overrightarrow {BC}  + \overrightarrow {BA} } \right) + \frac{1}{2}\left( {\overrightarrow {CA}  + \overrightarrow {CB} } \right)\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = \frac{1}{2}\left( {\overrightarrow {AC}  + \overrightarrow {AB}  + \overrightarrow {BC}  + \overrightarrow {BA}  + \overrightarrow {CA}  + \overrightarrow {CB} } \right)\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = \frac{1}{2}.\overrightarrow 0  = \overrightarrow 0 \end{array}$(đpcm)

b. Vì P là trung điểm của AB nên $\overrightarrow {AP}  = \overrightarrow {PB}$. Khi đó ta có $\overrightarrow {AP}  + \overrightarrow {BM}  = \overrightarrow {PB}  + \overrightarrow {BM}  = \overrightarrow {PM}$.

Mà PM là đường trung bình trong tam giác ABC nên suy ra $\overrightarrow {PM}  = \frac{1}{2}\overrightarrow {AC}$.

Suy ra $\overrightarrow {AP}  + \overrightarrow {BM}  = \frac{1}{2}\overrightarrow {AC}$ (đpcm).