Đề thi học kì 1 Toán 6 - Đề số 2 - Chân trời sáng tạo
Tải vềPhần I: Trắc nghiệm (4 điểm). Hãy chọn phương án trả lời đúng và viết chữ cái đứng trước đáp án đó vào bài làm.
Đề bài
Phần I: Trắc nghiệm (4 điểm).
Hãy chọn phương án trả lời đúng và viết chữ cái đứng trước đáp án đó vào bài làm.
Câu 1. Tìm cách viết đúng trong các cách viết sau?
A. \(3,2 \in \mathbb{N}\) B. \(0 \in {\mathbb{N}^*}\) C. \(0 \in \mathbb{N}\) D. \(0 \in \mathbb{N}\)
Câu 2. Số nào sau đây chia hết cho \(2\,;\,3\,;\,5\,;\,9\)?
A. \(39595\) B. \(39590\) C. \(39690\) D. \(39592\)
Câu 3. Kết quả của phép tính: \({3^{15}}:{9^3}\) là:
A. \({3^9}\) B. \({3^{12}}\) C. \({3^{18}}\) D. \({3^{21}}\)
Câu 4. Số nguyên \(x\) thỏa mãn: \(x - \left( { - 199} \right) = - 1\)
A. \(x = 198\) B. \(x = - 200\) C. \(x = 200\) D. \(x = - 198\)
Câu 5. Kết quả của phép tính nào dưới đây là số nguyên tố?
A. \({5^3} - {5^2}\) B. \({4^2} - {3^2}\) C. \({6^2} - {3^2}\) D. \({5^2} - {3^2}\)
Câu 6 . Khẳng định nào dưới đây là không đúng?
A. \(6 > 5\) B. \( - 6 < - 5\) C. \(6 > - 5\) D. \( - 6 > - 5\)
Câu 7. Hình vuông có cạnh là \(10\,\,cm\) thì chu vi của nó là:
A. \(40\,\,cm\) B. \(40\,\,c{m^2}\) C. \(100\,\,cm\) D. \(100\,\,c{m^2}\)
Câu 8: Một hiên nhà được thiết kế như hình vẽ bên. Hãy tính chi phí làm hiên nhà biết chi phí làm \(1\,\,{m^2}\) là \(120\,000\) đồng.
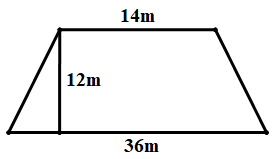
A. \(7\,440\,000\) đồng B. \(144\,000\,000\) đồng
C. \(36\,000\,000\) đồng D. \(72\,000\,000\) đồng
Câu 9. Trong các hình sau hình nào có diện tích bé nhất?
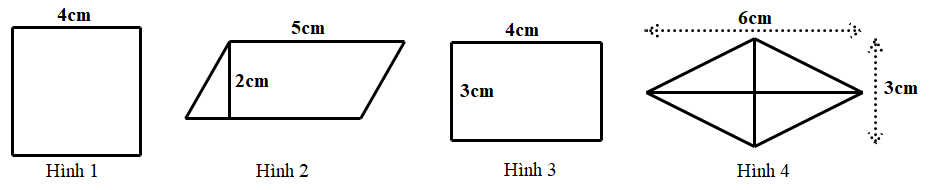
A. Hình 1 B. Hình 2 C. Hình 3 D. Hình 4
Câu 10. Cho biểu đồ cột kép biểu diễn số tiền Việt Nam thu được khi xuất khẩu cà phê và xuất khẩu gạo trong ba năm 2017, 2018, 2019.

Số tiền thu được khi xuất khẩu cà phê năm 2018 nhiều hơn số tiên thu được khi xuất khẩu cà phê năm 2019 là bao nhiêu?
A. \(0,67\) tỉ đô la Mỹ B. \(0,68\) tỉ đô la Mỹ C. \(0,69\) tỉ đô la Mỹ D. \(0,70\) tỉ đô la Mỹ
Phần II. Tự luận (6 điểm):
Bài 1. (1,5 điểm)
Thực hiện phép tính:
a) \(12:\left[ {450:\left( {125 + 25.4} \right)} \right]\) b) \({4.5^2} - {3^2}.\left( {{{2015}^0} + {1^{100}}} \right)\)
c) \(98.12345 + 12345.101 + 12345\)
Bài 2. (1,0 điểm)
Tìm \(x\), biết:
a) \(71 - \left( {33 + x} \right) = 26\) b) \({3^{4x + 1}} = {27^{x + 3}}\)
Bài 3. (1,0 điểm)
Tìm số tự nhiên \(x\), biết:
a) \(x\) lớn nhất và \(480\,\, \vdots \,\,x\,;\,\,600\,\, \vdots \,\,x\). b) \(x\,\, \vdots \,\,20,\,\,x\,\, \vdots \,\,35\) và \(x < 500\)
Bài 4. (2 điểm)
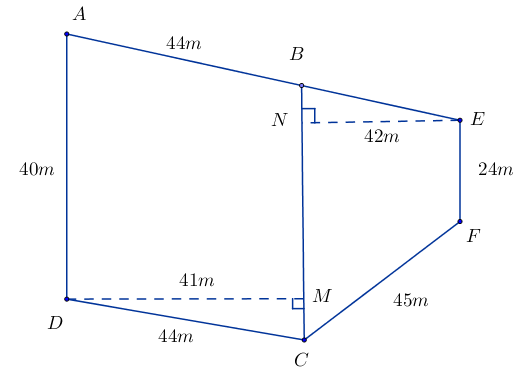
Để tính diện tích và chu vi mảnh đất có dạng như hình vẽ, người ta chia nó thành hình bình hành \(ABCD\) và hình thang cân \(BEFC\) có kích thước như sau: \(AD = 40m;EF = 24m;DC = 44m;DM = 41m;\) \(EN = 42m;\)\(CF = 45m\). Tính chu vi và diện tích mảnh đất này?
Bài 5. (0,5 điểm)
Cho: \(A = 1 + 3 + {3^2} + \ldots + {3^{11}}\). Chứng minh rằng: \(A\;\, \vdots \,\,13\)
Lời giải
Phần I: Trắc nghiệm
|
1. C |
2. C |
3. A |
4. B |
5. B |
6. D |
7. A |
8. C |
9. D |
10. C |
Câu 1
Phương pháp:
Nhận biết các phần tử thuộc tập hợp số tự nhiên.
Cách giải:
Ta có: số \(0\) thuộc tập hợp số tự nhiên nên cách viết \(0 \in \mathbb{N}\) là cách viết đúng
Chọn C.
Câu 2
Phương pháp:
Vận dụng dấu hiệu chia hết cho \(2\,;\,3\,;\,5\,;\,9\).
Cách giải:
Số chia hết cho \(2\,;\,5\) có chữ số tận cùng là \(0\), nên loại đáp án A và D
Ta kiểm tra hai số \(39590\) và \(39690\)
Ta có: \(3 + 9 + 5 + 9 + 0 = 26\not \vdots 9\)
\(3 + 9 + 6 + 9 + 0 = 27\not \vdots 9\) và \(27\not \vdots 3\)
Vậy số cần tìm là: \(39690\)
Chọn C.
Câu 3
Phương pháp:
Vận dụng quy tắc: \({\left( {{a^m}} \right)^n} = {a^{mn}}\)
Vận dụng quy tắc chia hai lũy thừa cùng cơ số: \({a^m}:{a^n} = {a^{m - n}}\,\,\left( {m \ge n} \right)\)
Cách giải:
Ta có: \({3^{15}}:{9^3} = {3^{15}}:{\left( {{3^2}} \right)^3} = {3^{15}}:{3^6} = {3^{15 - 6}} = {3^9}\)
Chọn A.
Câu 4
Phương pháp:
Vận dụng quy tắc bỏ ngoặc có dấu “\( - \)” ở trước, thực hiện phép trừ hai số nguyên âm.
Cách giải:
\(\begin{array}{l}x - \left( { - 199} \right) = - 1\\x + 199 = - 1\\x = \left( { - 1} \right) - 199\\x = \left( { - 1} \right) + \left( { - 199} \right)\\x = - 200\end{array}\)
Vậy \(x = - 200\)
Chọn B.
Câu 5
Phương pháp:
Vận dụng định nghĩa hợp số, số nguyên tố của số tự nhiên để phân được các kết quả của phép tính.
Cách giải:
Ta có:
\({5^3} - {5^2} = 125 - 25 = 100\) là hợp số nên không chọn đáp án A
\({4^2} - {3^2} = 16 - 9 = 7\) là số nguyên tố nên chọn B
\({6^2} - {3^2} = 36 - 9 = 27\) là hợp số nên không chọn đáp án C
\({5^2} - {3^2} = 25 - 9 = 16\) là hợp số nên không chọn đáp án D.
Chọn B.
Câu 6
Phương pháp:
Vận dụng kiến thức về số nguyên âm, số nguyên dương và số sánh các số nguyên với nhau.
Cách giải:
Vì \(6 > 5\) nên \( - 6 < - 5\) do đó đáp án D sai.
Chọn D.
Câu 7
Phương pháp:
Sử dụng công thức tính chu vi của hình vuông có cạnh là \(a\) là: \(P = 4.a\)
Cách giải:
Chu vi của hình vuông là: \(4.10 = 40\,\,\left( {cm} \right)\)
Chọn A.
Câu 8
Phương pháp:
Sử dụng công thức tính diện diện tích hình thang có độ dài hai đáy là \(a\,,\,b\) và có chiều cao là \(h\). Khi đó: \(S = \dfrac{{\left( {a + b} \right).h}}{2}\), tính diện tích của hiên nhà.
Chi phí làm hiên nhà = diện tích của hiên nhà \( \times \) chi phí của \(1\,{m^2}\)
Cách giải:
Diện tích của hiên nhà là: \(\dfrac{{\left( {14 + 36} \right).12}}{2} = 50.6 = 300\,\,\left( {{m^2}} \right)\)
Chi phí làm hiên nhà là: \(300.120\,000 = 36\,000\,000\) (đồng)
Chọn C.
Câu 9
Phương pháp:
Vận dụng công thức tính diện tích:
+ Hình vuông có cạnh bằng \(a\) thì \(S = a.a\)
+ Hình bình hành có độ dài hai cạnh đáy là \(a,b\), độ dài đường cao tương ứng với cạnh \(a\) là \(h\) thì \(S = a.h\).
+ Hình chữ nhật có độ dài hai cạnh là \(a,b\) thì \(S = a.b\)
+ Hình thoi có độ dài hai đường chéo \(m,n\) là \(S = \dfrac{1}{2}m.n\).
Cách giải:
Diện tích hình 1 là: \(4.4 = 16\,\left( {c{m^2}} \right)\)
Diện tích hình 2 là: \(2.5 = 10\,\left( {c{m^2}} \right)\)
Diện tích hình 3 là: \(3.4 = 12\,\left( {c{m^2}} \right)\)
Diện tích hình 4 là: \(\dfrac{1}{2}.3.6 = 9\,\left( {c{m^2}} \right)\)
Ta có: \(9 < 10 < 12 < 16\)
Vậy diện tích hình 4 là bé nhất.
Chọn D.
Câu 10
Phương pháp:
Sử dụng lý thuyết biểu đồ cột kép.
Cách giải:
Số tiền thu được khi xuất khẩu cà phê năm 2018 nhiều hơn số tiên thu được khi xuất khẩu cà phê năm 2019 là: \(3,54 - 2,85 = 0,69\) (tỉ đô la Mỹ) Chọn C.
Phần II: Tự luận
Bài 1
Phương pháp:
Sử dụng thứ tự thực hiện phép tính đối với biểu thức có dấu ngoặc: \(\left( {} \right) \to \left[ {} \right] \to \left\{ {} \right\}\)
Vận dụng kiến thức lũy thừa của một số tự nhiên
Cách giải:
|
a) \(12:\left[ {450:\left( {125 + 25.4} \right)} \right]\) \(\begin{array}{l} = 12:\left[ {450:\left( {125 + 100} \right)} \right]\\ = 12:\left[ {450:225} \right]\\ = 12:2\\ = 6\end{array}\) |
b) \({4.5^2} - {3^2}.\left( {{{2015}^0} + {1^{100}}} \right)\) \(\begin{array}{l} = 4.25 - 9.\left( {1 + 1} \right)\\ = 100 - 9.2\\ = 100 - 18\\ = 82\end{array}\) |
c)
\(\begin{array}{l}98.12345 + 12345.101 + 12345\\ = 12345.\left( {98 + 101 + 1} \right)\\ = 12345.200\\ = 2469000\end{array}\)
Bài 2
Phương pháp:
Giải bài toán ngược để tìm \(x\)
Vận dụng kiến thức về lũy thừa với số tự nhiên, so sánh lũy thừa cùng cơ số để tìm \(x\).
Cách giải:
|
a) \(71 - \left( {33 + x} \right) = 26\) \(\begin{array}{l}33 + x = 71 - 26\\33 + x = 45\\x = 45 - 33\\x = 12\end{array}\) Vậy \(x = 12\) |
b) \({3^{4x + 1}} = {27^{x + 3}}\) \(\begin{array}{l}{3^{4x + 1}} = {3^{3\left( {x + 3} \right)}}\\4x + 1 = 3(x + 3)\\4x + 1 = 3x + 9\\4x - 3x = 9 - 1\\x = 8\end{array}\) Vậy \(x = 8\). |
Bài 3
Phương pháp:
a) Vận dụng quy tắc tìm ước chung lớn nhất của hai số.
b) Vận dụng quy tắc tìm bội chung nhỏ nhất của hai số.
Cách giải:
a) Vì \(x\) lớn nhất và \(480\,\, \vdots \,\,x\,;\,\,600\,\, \vdots \,\,x\) \( \Rightarrow x = \)ƯCLN\(\left( {480,600} \right)\)
Ta có: \(\left\{ \begin{array}{l}480 = {2^5}.3.5\\600 = {2^3}{.3.5^2}\end{array} \right. \Rightarrow \)ƯCLN\(\left( {480,600} \right) = {2^3}.3.5 = 120\)
Vậy \(x = 120\)
b) Vì \(x\,\, \vdots \,\,20,\,\,x\,\, \vdots \,\,35\) \( \Rightarrow x \in \)BC\(\left( {20;35} \right)\)
Ta có: \(\left\{ \begin{array}{l}20 = {2^2}.5\\35 = 5.7\end{array} \right. \Rightarrow \)BCNN\(\left( {20,35} \right) = {2^2}.5.7 = 140\)
\( \Rightarrow \)BC\(\left( {20,35} \right) = \)B\(\left( {140} \right) = \left\{ {0;140;280;420;560;...} \right\}\)
Mà \(x < 500 \Rightarrow x \in \left\{ {0;140;280;420} \right\}\)
Vậy \(x \in \left\{ {0;140;280;420} \right\}\).
Bài 4
Phương pháp:
Tính diện tích của hình bình hành \(ABCD\)
Tính diện của hình thang cân \(BEFC\)
\( \Rightarrow \) Tính diện tích của mảnh đất
Tính chu vi của mảnh đất: \(AE + EF + FC + CD + DA\)
Cách giải:
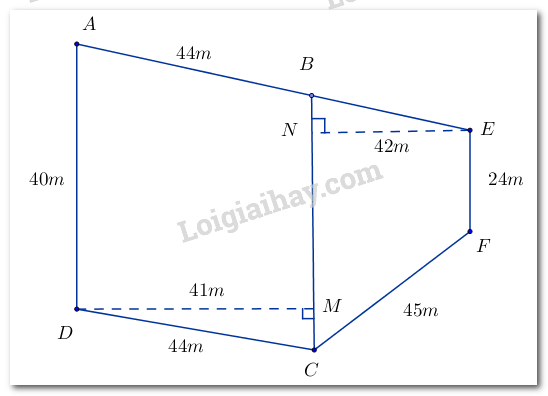
* Diện tích của hình bình hành \(ABCD\) là: \(DM.BC = 41.40 = 1640\left( {{m^2}} \right)\)
Diện tích của hình thang cân\(BEFC\) là: \(\dfrac{{\left( {EF + BC} \right).EN}}{2} = \dfrac{{\left( {24 + 40} \right).42}}{2} = 1344\left( {{m^2}} \right)\)
Diện tích của mảnh đất là: \(1640 + 1344 = 2984\left( {{m^2}} \right)\)
* Ta có: \(AB = CD = 44\left( m \right);BE = CF = 45\left( m \right)\)
Chu vi của mảnh đất là: \(AE + EF + FC + CD + DA\)
\(\begin{array}{l} = AB + BE + EF + FC + CD + DA\\ = 44 + 45 + 24 + 45 + 44 + 40 = 242\left( {{m^2}} \right)\end{array}\)
Bài 5
Phương pháp:
Sử dụng tính chất chia hết của một tích, nhóm các hạng tử để xuất hiện thừa số \(13\).
Cách giải:
\(\begin{array}{l}A\; = 1 + 3 + {3^2} + {3^{3\;}} + \ldots + {3^{11}}\\A\; = \left( {1 + 3 + {3^2}} \right) + \left( {{3^3} + {3^4} + {3^5}} \right) + \ldots + \left( {{3^9} + {3^{10}}{\rm{ + }}{3^{11}}} \right)\\A\; = \left( {1 + 3 + {3^2}} \right) + {3^3}.\left( {1 + 3 + {3^2}} \right) + \ldots + {3^9}.\left( {1 + 3 + {3^2}} \right)\\A\; = 13\; + \;{3^3}.13\; + \ldots + {3^9}.13\\A\; = 13.\left( {1 + {3^3} + \ldots + {3^9}} \right)\;\\ \Rightarrow A\,\, \vdots \,\,13\end{array}\)