Đề thi giữa kì 2 Toán 6 Chân trời sáng tạo - Đề số 10
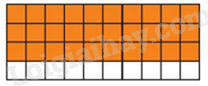
Phần trắc nghiệm (3 điểm) Câu 1 (NB): Phân số nào dưới đây không biểu diễn phần tô màu cam trong hình bên:
Đề bài
-
A.
\(\frac{{30}}{{40}}\)
-
B.
\(\frac{1}{4}\).
-
C.
\(\frac{3}{4}\)
-
D.
\(\frac{6}{8}\)
Giá trị \(\frac{3}{4}\) của – 60 là:
-
A.
80.
-
B.
- 80.
-
C.
45.
-
D.
- 45.
Hai phân số \(\frac{a}{b} = \frac{3}{4}\) khi
-
A.
\(a.3 = b.4\).
-
B.
\(a.4 = 3.b\).
-
C.
\(a + 4 = b + 3\).
-
D.
\(a - 4 = b - 3\).
Khi rút gọn phân \(\frac{{ - 27}}{{63}}\) ta được phân số tối giản là số nào sau đây?
-
A.
\(\frac{9}{{21}}\).
-
B.
\(\frac{{ - 3}}{7}\).
-
C.
\(\frac{3}{7}\).
-
D.
\(\frac{{ - 9}}{{21}}\).
-
A.
Hình 1.
-
B.
Hình 2.
-
C.
Hình 3.
-
D.
Hình 4.
-
A.
0.
-
B.
1.
-
C.
2.
-
D.
3.
Trong tự nhiên, hình nào trong các hình dưới đây không có tâm đối xứng
-
A.

-
B.

-
C.

-
D.

Chọn phát biểu sai. Khi O là trung điểm của đoạn AB thì
-
A.
A đối xứng với B qua O.
-
B.
Điểm đối xứng với O qua O là chính nó.
-
C.
A không phải là điểm đối xứng của B qua O.
-
D.
A và B đều đúng.
-
A.
Điểm A.
-
B.
Điểm B và điểm C.
-
C.
Điểm B và điểm D.
-
D.
Điểm D và điểm C.
Cho F là điểm nằm giữa hai điểm P và Q. Khi đó tia đối của tia FQ là
-
A.
tia QF.
-
B.
tia QP.
-
C.
tia FP.
-
D.
tia PF.
Em hãy chọn câu đúng.
-
A.
Qua hai điểm phân biệt có vô số đường thẳng.
-
B.
Có vô số điểm cùng thuộc một đường thẳng.
-
C.
Hai đường thẳng phân biệt thì song song.
-
D.
Trong ba điểm thẳng hàng thì có hai điểm nằm giữa.
-
A.
Hai đường thẳng AB và AC cắt nhau.
-
B.
Hai đường thẳng AB và AC song song với nhau.
-
C.
Hai đường thẳng AB và AC trùng nhau.
-
D.
Hai đường thẳng AB và AC có hai điểm chung.
Lời giải và đáp án
-
A.
\(\frac{{30}}{{40}}\)
-
B.
\(\frac{1}{4}\).
-
C.
\(\frac{3}{4}\)
-
D.
\(\frac{6}{8}\)
Đáp án : B
Quan sát hình vẽ và tìm các phân số bằng với phân số đó..
Ta thấy trong hình có 40 ô và có 30 ô màu cam nên ta có phân số biểu diễn phần tô màu cam trong hình bên là \(\frac{{30}}{{40}}\).
Các phân số bằng với phân số \(\frac{{30}}{{40}}\) là \(\frac{3}{4}\) và \(\frac{6}{8}\).
Vậy phân số không biểu diễn là phân số \(\frac{1}{4}\).
Đáp án B.
Giá trị \(\frac{3}{4}\) của – 60 là:
-
A.
80.
-
B.
- 80.
-
C.
45.
-
D.
- 45.
Đáp án : D
Tính \(\frac{m}{n}\) của a bằng \(a.\frac{m}{n}\).
Giá trị \(\frac{3}{4}\) của – 60 là: \(\left( { - 60} \right).\frac{3}{4} = - 45\).
Đáp án D.
Hai phân số \(\frac{a}{b} = \frac{3}{4}\) khi
-
A.
\(a.3 = b.4\).
-
B.
\(a.4 = 3.b\).
-
C.
\(a + 4 = b + 3\).
-
D.
\(a - 4 = b - 3\).
Đáp án : B
Hai phân số \(\frac{a}{b} = \frac{c}{d}\) khi \(ad = bc\).
Hai phân số \(\frac{a}{b} = \frac{3}{4}\) khi \(a.4 = 3.b\) .
Đáp án B.
Khi rút gọn phân \(\frac{{ - 27}}{{63}}\) ta được phân số tối giản là số nào sau đây?
-
A.
\(\frac{9}{{21}}\).
-
B.
\(\frac{{ - 3}}{7}\).
-
C.
\(\frac{3}{7}\).
-
D.
\(\frac{{ - 9}}{{21}}\).
Đáp án : B
Sử dụng quy tắc rút gọn phân số.
\(\frac{{ - 27}}{{63}} = \frac{{ - 27:9}}{{63:9}} = \frac{{ - 3}}{7}\).
Đáp án B.
-
A.
Hình 1.
-
B.
Hình 2.
-
C.
Hình 3.
-
D.
Hình 4.
Đáp án : A
Dựa vào kiến thức về trục đối xứng.
Hình có trục đối xứng là hình 1.
Đáp án A.
-
A.
0.
-
B.
1.
-
C.
2.
-
D.
3.
Đáp án : D
Dựa vào kiến thức về trục đối xứng.
Cả ba công trình trên đều có trục đối xứng.

Đáp án D.
Trong tự nhiên, hình nào trong các hình dưới đây không có tâm đối xứng
-
A.

-
B.

-
C.

-
D.

Đáp án : B
Dựa vào kiến thức về tâm đối xứng.
Trong các hình này, hình không có tâm đối xứng là hình sao biển.

Đáp án B.
Chọn phát biểu sai. Khi O là trung điểm của đoạn AB thì
-
A.
A đối xứng với B qua O.
-
B.
Điểm đối xứng với O qua O là chính nó.
-
C.
A không phải là điểm đối xứng của B qua O.
-
D.
A và B đều đúng.
Đáp án : C
Dựa vào kiến thức về tính đối xứng.
O là trung điểm của AB thì A đối xứng với B qua O nên A đúng C sai.
O đối xứng với O qua chính nó nên B đúng.
Đáp án C.
-
A.
Điểm A.
-
B.
Điểm B và điểm C.
-
C.
Điểm B và điểm D.
-
D.
Điểm D và điểm C.
Đáp án : B
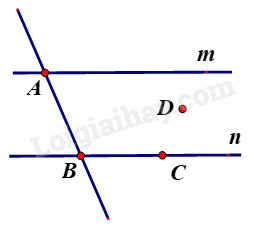
Quan sát hình vẽ để trả lời.
Đường thẳng n đi qua điểm B và điểm C
Đáp án B.
Cho F là điểm nằm giữa hai điểm P và Q. Khi đó tia đối của tia FQ là
-
A.
tia QF.
-
B.
tia QP.
-
C.
tia FP.
-
D.
tia PF.
Đáp án : C
Dựa vào kiến thức về tia đối.
Tia đối của tia FQ là tia FP (vì F nằm giữa P và Q).
Đáp án C.
Em hãy chọn câu đúng.
-
A.
Qua hai điểm phân biệt có vô số đường thẳng.
-
B.
Có vô số điểm cùng thuộc một đường thẳng.
-
C.
Hai đường thẳng phân biệt thì song song.
-
D.
Trong ba điểm thẳng hàng thì có hai điểm nằm giữa.
Đáp án : B
Dựa vào kiến thức về đường thẳng.
Qua hai điểm phân biệt chỉ có 1 đường thẳng nên A sai.
Có vô số điểm cùng thuộc một đường thẳng. nên B đúng.
Hai đường thẳng phân biết chưa chắc đã song song nên C sai.
Trong ba điểm thẳng hàng chỉ có một điểm nằm giữa nên D sai.
Đáp án B.
-
A.
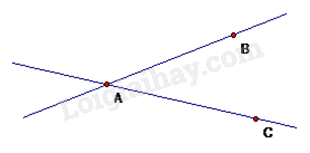
Hai đường thẳng AB và AC cắt nhau.
-
B.
Hai đường thẳng AB và AC song song với nhau.
-
C.
Hai đường thẳng AB và AC trùng nhau.
-
D.
Hai đường thẳng AB và AC có hai điểm chung.
Đáp án : A
Quan sát hình vẽ để xác định.
Hai đường thẳng AB và AC cắt nhau tại A.
Đáp án A.
Dựa vào quy tắc tính với phân số.
a) \(\frac{{ - 3}}{7} + \frac{5}{7} = \frac{2}{7}\)
b) \(\frac{2}{3} + \frac{{ - 3}}{5} = \frac{{10}}{{15}} + \frac{{ - 9}}{{15}} = \frac{1}{{15}}\)
c) \(\frac{2}{9} - \left( {\frac{1}{{20}} + \frac{2}{9}} \right) = \frac{2}{9} - \frac{1}{{20}} - \frac{2}{9} = - \frac{1}{{20}}\)
d) \(\frac{{11}}{{23}}.\frac{{12}}{{17}} + \frac{{11}}{{23}}.\frac{5}{{17}} + \frac{{12}}{{23}}\)\( = \frac{{11}}{{23}}.\left( {\frac{{12}}{{17}} + \frac{5}{{17}}} \right) + \frac{{12}}{{23}}\) \( = \frac{{11}}{{23}} \cdot 1 + \frac{{12}}{{23}}\)\( = \frac{{23}}{{23}}\)\( = 1\)
Dựa vào kiến thức về trục đối xứng, tâm đối xứng để xác định.
a) Ta vẽ được đường thẳng d là trục đối xứng của Hình 1 như sau:
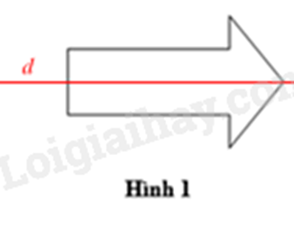
b) Tâm đối xứng I của hình 2 là giao điểm của các đoạn thẳng nối các chấm cùng màu.
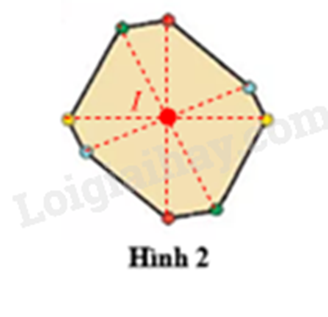
Áp dụng cách tính \(\frac{m}{n}\) của a bằng \(a.\frac{m}{n}\).
Số gạo ngày thứ hai bán được là: \(\frac{4}{9}.\left( {1 - \frac{1}{3}} \right) = \frac{8}{{27}}\) (tổng số gạo)
1400kg gạo tương ứng với phân số \(1 - \frac{1}{3} - \frac{8}{{27}} = \frac{{10}}{{27}}\) (tổng số gạo).
Số gạo bán được trong 3 ngày là: \(1400:\frac{{10}}{{27}} = 3780\) (kg)
Vậy số gạo bán được trong cả ba ngày là 3780kg.
Vẽ hình theo yêu cầu.
a) Chứng minh OA < OB nên A nằm giữa O và B.
b) Tính KA dựa vào KO và OA. So sánh KA và AB.

a) Trên tia Ox ta có OA = 3cm, OB = 6cm vì 3 < 6 nên OA < OB
Do đó A nằm giữa O và B. (1)
Suy ra: OA + AB = OB
Thay số ta được 3 + AB = 6
Suy ra AB = 3(cm)
Mà OA = 3(cm) nên OA = AB (2)
Từ (1) và (2) suy ra: A là trung điểm của OB (đpcm)
b) Ta có A thuộc tia Ox, K thuộc tia đối của tia Ox nên A và K nằm khác phía đối với O hay O nằm giữa K và A.
Suy ra KO + OA = KA.
Thay số ta được 1 + 3 = KA
Suy ra KA = 4(cm).
Mà AB = 3cm nên KA > AB (do 4 > 3).
Vậy KA > AB.
Tính chiều rộng của mảnh vườn theo chiều dài.
Sử dụng công thức tính diện tích hình chữ nhật để tính diện tích mảnh vườn.
Chiều rộng của mảnh vườn là:
\(10.\frac{3}{5} = 6\left( m \right)\)
Diện tích của mảnh vườn là:
\(10.6 = 60\left( {{m^2}} \right)\)
Vậy diện tích mảnh vườn là \(60{m^2}\).