Đề thi học kì 1 Toán 6 - Đề số 8 - Kết nối tri thức
Tải vềPhần I: Trắc nghiệm (2 điểm). Hãy chọn phương án trả lời đúng và viết chữ cái đứng trước đáp án đó vào bài làm.
Đề bài
Phần I: Trắc nghiệm (2 điểm). Hãy chọn phương án trả lời đúng và viết chữ cái đứng trước đáp án đó vào bài làm.
Câu 1: Tập hợp A gồm các số tự nhiên không vượt quá 6 được viết là:
A. \(A = \left\{ {1;2;3;4;5} \right\}\) B. \(A = \){x| x là số tự nhiên, x < 6}
C. \(A = \){\(x\) |\(x\) là số tự nhiên, \(x \le 6\)} D. \(A = \){\(x\) |\(x\) là số tự nhiên, \(x \ge 6\)}
Câu 2: Trong các tập hợp sau, tập hợp nào có các số nguyên được sắp xếp theo thứ tự tăng dần?
A. \(\left\{ {3; - 13;5;1; - 2;0} \right\}\) B. \(\left\{ {0;1; - 2;3;5; - 13} \right\}\)
C. \(\left\{ { - 2; - 13;5;3;1;0} \right\}\) D. \(\left\{ { - 13; - 2;0;1;3;5} \right\}\)
Câu 3: BCNN của \({2^3}.3.5\) và \({2.3^2}.5\) là:
A. \(480\) B. \(360\) C. \(380\) D. \(540\)
Câu 4: Tổng các số nguyên x thoả mãn \( - 10 \le x < 11\)bằng:
A. \(11\) B. \(0\) C. \(1\) D. \( - 10\)
Câu 5: Số tự nhiên \(x\) để \(\left( {32 - x} \right)\) là số liền trước của 21 là
A. \(12\) B. \(20\) C. \(22\) D. \(52\)
Câu 6: Trong các hình dưới đây, hình nào là hình thang cân?
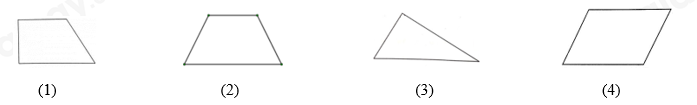
A. Hình (3) B. Hình (1) C. Hình (2) D. Hình (4)
Câu 7: Hình thoi có độ dài hai đường chéo lần lượt là 6 cm và 8 cm thì diện tích của nó là
A. 24 cm 2 B. 7 cm 2 C. 14 cm 2 D. 48 cm 2
Câu 8: Hình nào dưới đây không có trục đối xứng?

(1) (2) (3) (4)
A. Hình (2) B. Hình (3) C. Hình (4) D. Hình (1)
Phần II. Tự luận (8 điểm):
Câu 1: (2 điểm) Thực hiện các phép tính:
a) \(\left( { - 17} \right) + 54 + 17\)
b) \({5^{10}}:{5^8} + 60:12 + \left( { - 10} \right)\)
c) \(\left\{ {240 - \left[ {76 - {{\left( {9 - 3} \right)}^2}} \right]} \right\}:50\)
Câu 2: (1,5 điểm) Tìm x biết:
a) \(x - 17 = - 15\) b) \(\left( {x + 3} \right).20 - 5 = 75\)
Câu 3: (1,5 điểm) Hai lớp 6A và 6B tham gia phong trào trồng cây của toàn trường. Lớp 6A trồng được 132 cây, lớp 6B trồng được 135 cây. Biết rằng, mỗi bạn trong cả hai lớp đều trồng được một số cây như nhau và trồng được nhiều hơn 2 cây.
a) Hỏi mỗi bạn của hai lớp trồng được bao nhiêu cây?
b) Tính số học sinh của mỗi lớp?
Câu 4: (2,5 điểm) Cho hình thang cân MNPQ có độ dài đáy MN = 4cm, độ dài đáy QP gấp 3 lần độ dài đáy MN. Độ dài chiều cao MH = 3 cm, cạnh bên NP = 5 cm.
a) Tính độ dài đáy QP.
b) Tính diện tích hình thang MNPQ.
c) Tính chu vi hình thang MNPQ.
Câu 5: (0,5 điểm) Chứng minh rằng: \(\forall n \ge 1\), ta có: \(3{n^4} - 14{n^3} + 21{n^2} - 10n\,\, \vdots \,\,24.\)
Lời giải
Phần I: Trắc nghiệm
|
1.C |
2.D |
3.B |
4.B |
5.A |
6.C |
7.A |
8.A |
Câu 1
Phương pháp:
“không vượt quá” tức là “nhỏ hơn hoặc bằng”.
Viết tập hợp bằng cách liệt kê các phần tử của tập hợp hoặc chỉ ra tính chất đặc trưng của phần tử.
Cách giải:
\(A = \){\(x\) |\(x\) là số tự nhiên, \(x \le 6\)}.
Chọn C.
Câu 2
Phương pháp:
Sử dụng kiến thức thứ tự trong tập hợp số nguyên.
Cách giải:
Ta có: \( - 13 < - 2 < 0 < 1 < 3 < 5\)
Nên chọn \(\left\{ { - 13; - 2;0;1;3;5} \right\}\)
Chọn D.
Câu 3
Phương pháp:
Sử dụng phương pháp tìm bội chung nhỏ nhất của hai số:
- Chọn các thừa số nguyên tố chung và các thừa số nguyên tố riêng;
- Với mỗi thừa số nguyên tố chung và riêng, ta chọn luỹ thừa với số mũ lớn nhất;
- Lấy tích của các luỹ thừa đã chọn, ta nhận được bội chung nhỏ nhất.
Cách giải:
BCNN của \({2^3}.3.5\) và \({2.3^2}.5\) là: \({2^3}{.3^2}.5 = 360.\)
Chọn B.
Câu 4
Phương pháp:
Tìm các giá trị của x thoả mãn \( - 10 \le x < 11\).
Tính tổng bằng cách nhóm các cặp số đối nhau.
Cách giải:
Ta có: \( - 10 \le x < 11\) suy ra \(x \in \left\{ { - 10; - 9; - 8;...;8;9;10} \right\}\)
\(\left( { - 10} \right) + \left( { - 9} \right) + \left( { - 8} \right) + ... + 8 + 9 + 10 = \left[ {\left( { - 10} \right) + 10} \right] + \left[ {\left( { - 9} \right) + 9} \right] + ... = 0\)
Chọn B.
Câu 5
Phương pháp:
Số liền trước của 21 là 20.
Tìm \(x\) để \(32 - x = 20\).
Cách giải:
Ta có: Số liền trước của 21 là 20.
\(32 - x = 20\)
\(x\,\,\,\,\,\,\,\,\,\,\,\, = 32 - 20\)
\(x\,\,\,\,\,\,\,\,\,\,\,\, = 12\)
Chọn A.
Câu 6
Phương pháp:
Quan sát và nhận dạng hình thang cân.
Cách giải:
Hình thang cân có hai góc ở đáy bằng nhau, hai cạnh bên bằng nhau.
Chọn C.
Câu 7
Phương pháp:
Diện tích hình thoi bằng tích hai đường chéo chia 2.
Cách giải:
Diện tích hình thoi là \(\dfrac{1}{2}.6.8 = 24\,c{m^2}\).
Chọn A.
Câu 8
Phương pháp:
Quan sát dựa vào hình có trục đối xứng.
Cách giải:
Hình (1): hình bình hành không có trục đối xứng.
Chọn A.
Phần II: Tự luận
Câu 1:
Phương pháp:
Thực hiện các phép tính theo đúng thứ tự.
Sử dụng các tính chất của phép cộng, phép nhân để tính hợp lí.
Cách giải:
a) \(\left( { - 17} \right) + 54 + 17 = \left[ {\left( { - 17} \right) + 17} \right] + 54 = 0 + 54 = 54\).
b) \({5^{10}}:{5^8} + 60:12 + \left( { - 10} \right) = {5^2} + 5 + \left( { - 10} \right) = 25 + 5 + \left( { - 10} \right) = 30 + \left( { - 10} \right) = 20.\)
c) \(\left\{ {240 - \left[ {76 - {{\left( {9 - 3} \right)}^2}} \right]} \right\}:50\)
\( = \left\{ {240 - \left[ {76 - {6^2}} \right]} \right\}:50\)
\( = \left\{ {240 - \left[ {76 - 36} \right]} \right\}:50\)
\( = \left\{ {240 - 40} \right\}:50\)
\( = 200:50 = 4\)
Câu 2:
Phương pháp:
a) Sử dụng quy tắc chuyển vế.
b) Chuyển \( - 5\) sang vế phải; tìm \(x + 3\); giải tìm x như phần a.
Cách giải:
a) \(x - 17 = - 15\)
\(\,\,\,\,\,\,x\,\,\,\,\,\,\,\,\,\,\, = - 15 + 17\)
\(\,\,\,\,\,\,x\,\,\,\,\,\,\,\,\,\,\, = 2\)
b) \(\left( {x + 3} \right).20 - 5 = 75\)
\(\,\,\,\,\,\,\left( {x + 3} \right).20\,\,\,\,\,\,\, = 75 + 5\)
\(\,\,\,\,\,\,\left( {x + 3} \right).20\,\,\,\,\,\,\, = 80\)
\(\,\,\,\,\,\,\,\,x + 3\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = 80:20\)
\(\,\,\,\,\,\,\,\,x + 3\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = 4\)
\(\,\,\,\,\,\,\,\,x\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = 4 - 3\)
\(\,\,\,\,\,\,\,\,x\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = 1\)
Câu 3:
Phương pháp:
Số cây mỗi bạn trồng được là ước chung lớn hơn 2 của 132 và 135.
Giải bài toán tìm ước chung.
Đưa ra lời giải cho bài toán.
Cách giải:
a) Gọi số cây mỗi bạn của hai lớp trồng được là \(x,\,\,\left( {x \in \mathbb{N}*} \right)\).
Mỗi bạn trong cả hai lớp đều trồng được một số cây như nhau nên ta có \(x\)thuộc ước chung của 132 và 135.
\(132 = {2^2}.3.11;\,\,135 = {3^3}.5\)
ƯCLN(132; 135) = 3.
Suy ra ƯC(132;135) = {1;3}
Mà \(x > 2\)
Nên \(x = 3\).
Vậy số cây mỗi bạn của hai lớp trồng được là 3.
b) Số học sinh của lớp 6A là: \(132:3 = 44\)(học sinh).
Số học sinh của lớp 6B là: \(135:3 = 45\)(học sinh).
Câu 4:
Phương pháp:
a) Tính độ dài đáy QP bằng 3 lần độ dài đáy MN.
b) Diện tích hình thang tính bằng công thức: (đáy lớn + đáy nhỏ) . chiều cao : 2
c) Chu vi hình thang bằng tổng độ dài các cạnh.
Cách giải:
a) Độ dài đáy PQ là: \(3.4 = 12\)cm.
b) Diện tích hình thang MNPQ là: \((4 + 12).3:2 = 24\,\,c{m^2}\).
c) Ta có MNPQ là hình thang cân nên độ dài hai cạnh bên NP và MQ là bằng nhau.
Suy ra độ dài cạnh MQ bằng 5 cm.
Chu vi hình thang MNPQ là: \(5 + 4 + 12 + 5 = 26\)cm.
Câu 5:
Phương pháp:
Sử dụng phương pháp quy nạp.
Sử dụng:
\(\begin{array}{l}{\left( {k + 1} \right)^4} = {k^4} + 4{k^3} + 6{k^2} + 4k + 1\\{\left( {k + 1} \right)^3} = {k^3} + 3{k^2} + 3k + 1\\{\left( {k + 1} \right)^2} = {k^2} + 2k + 1\end{array}\)
Cách giải:
Ta có: \(3{n^4} - 14{n^3} + 21{n^2} - 10n\,\, \vdots \,\,24\,\,\,\left( 1 \right)\,\,\,\)
+) Với \(n = 1\) ta có: \(3 - 14 + 21 - 10 = 0\,\, \vdots \,\,24\) (đúng)
+) Giả sử \(\left( 1 \right)\) đúng với \(n = k,\,\,\,k \ge 1\) nghĩa là :\(3{k^4} - 14{k^3} + 21{k^2} - 10k \vdots 24\) \(\left( 2 \right)\) (giả thiết quy nạp)
Ta phải chứng minh \(\left( 1 \right)\) đúng vói \(n = k + 1\) nghĩa là :\(3{\left( {k + 1} \right)^4} - 14{\left( {k + 1} \right)^3} + 21{\left( {k + 1} \right)^2} - 10\left( {k + 1} \right) \vdots 24\)
\(\begin{array}{l}\,\,\,\,\,3{\left( {k + 1} \right)^4} - 14{\left( {k + 1} \right)^3} + 21{\left( {k + 1} \right)^2} - 10\left( {k + 1} \right)\\ = 3\left( {{k^4} + 4{k^3} + 6{k^2} + 4k + 1} \right) - 14\left( {{k^3} + 3{k^2} + 3k + 1} \right) + 21\left( {{k^2} + 2k + 1} \right) - 10\left( {k + 1} \right)\\ = 3{k^4} + 12{k^3} + 18{k^2} + 12k + 3 - 14{k^3} - 42{k^2} - 42k - 14 + 21{k^2} + 42k + 21 - 10k - 10\\ = \left( {3{k^4} - 14{k^3} + 21{k^2} - 10k} \right) + \left( {12{k^3} + 18{k^2} + 12k + 3 - 42{k^2} - 42k - 14 + 42k + 21 - 10} \right)\\ = \left( {3{k^4} - 14{k^3} + 21{k^2} - 10k} \right) + \left( {12{k^3} - 24{k^2} + 12k} \right)\\ = \left( {3{k^4} - 14{k^3} + 21{k^2} - 10k} \right) + 12k\left( {{k^2} - 2k + 1} \right)\\ = \left( {3{k^4} - 14{k^3} + 21{k^2} - 10k} \right) + 12k\left( {k - 1} \right)\left( {k - 1} \right)\end{array}\)
Vì \(\left( {3.{k^4} - 14{k^3} + 21{k^2} - 10k} \right)\,\, \vdots \,\,24\) theo \(\left( 2 \right)\)
Vì \(k\left( {k - 1} \right)\,\, \vdots \,\,2 \Rightarrow 12k\left( {k - 1} \right)\left( {k - 1} \right)\,\, \vdots \,\,24.\)
\( \Rightarrow \left( {3.{k^4} - 14{k^3} + 21{k^2} - 10k} \right) + 12k\left( {k - 1} \right)\left( {k - 1} \right)\,\, \vdots \,\,24\)
\( \Rightarrow \left( 1 \right)\) đúng với \(n = k + 1\)
Vậy \(3{n^4} - 14{n^3} + 21{n^2} - 10n\,\, \vdots \,\,24\,\,\,\forall n \ge 1\) (đpcm).