Đề thi học kì 1 Toán 6 - Đề số 11 - Kết nối tri thức — Không quảng cáo

Dựa vào kiến thức về các tập hợp.

Tập hợp số tự nhiên được kí hiệu là \(\mathbb{N}\).

Dựa vào kiến thức về số nguyên âm.

Số nguyên âm có hai chữ số lớn nhất là -10.

Dựa vào kiến thức về số nguyên âm, số nguyên dương.

Ta có:

+) 44 > 34 nên – 44 < - 34.

+) -3 < 0 < 3 nên -3 < 3.

+) -10 < 0.

+) 9 > 8 nên -9 < -8.

Vậy chỉ có D sai.

Dựa vào kiến thức về tâm đối xứng của hình thoi.

Tâm đối xứng của hình thoi là giao điểm của hai đường chéo .

Dựa vào công thức tính diện tích hình bình hành: S = cạnh.chiều cao tương ứng.

Diện tích hình bình hành đó là: \(S = 8.5 = 40\left( {c{m^2}} \right)\).

Sử dụng quy tắc nhân hai số nguyên khác dấu.

Ta có: (-5).4 = -(5.4) = -20.

Kiểm tra xem 8 chia hết cho số nào có trong đáp án.

Ta có: \(8 \vdots 4;8 \not \vdots 5;8\not \vdots 6\); 0 không phải là ước của số nào nên A đúng.

Dựa vào kiến thức về trục đối xứng: Có một đường thẳng d chia hình thành hai phần mà khi ta “ gấp ” hình theo đường thẳng d thì hai phần đó “ chồng khít ” lên nhau .

Dựa vào kiến thức về tâm đối xứng: Những hình có một điểm O sao cho khi quay nửa vòng quanh điểm O ta được vị trí mới của hình chồng khít với vị trí ban đầu (trước khi quay) thì được gọi là hình có tâm đối xứng và điểm O được gọi là tâm đối xứng của hình.

Các chữ cái có trục đối xứng là A; M; X; U.

Các chữ cái có tâm đối xứng là: X.

Vậy chữ X vừa có tâm đối xứng, vừa có trục đối xứng.

Dựa vào dấu hiệu chia hết cho 3: Các số có tổng các chữ số chia hết cho 3 thì số đó chia hết cho 3 và chỉ những số đó chia hết cho 3.

Để số \(\overline {47x} \) chia hết cho 3 thì 4 + 7 + x chia hết cho 3 hay 11 + x chia hết cho 3.

x có thể nhận các giá trị: 1; 4; 7. Vậy ta chọn đáp án D.

Dựa vào đặc điểm của các hình đã học.

Trong các khẳng định sau, chỉ có khẳng định: “Hình chữ nhật có 2 đường chéo bằng nhau” là khẳng định đúng.

Muốn tìm BCNN của hai hay nhiều số lớn hơn 1, ta thực hiện theo ba bước sau :

Bước 1 : Phân tích mỗi số ra thừa số nguyên tố.

Bước 2 : Chọn ra các thừa số nguyên tố chung và riêng .

Bước 3 : Lập tích các thừa số đã chọn , mỗi thừa số lấy với số mũ lớn nhất của nó. Tích đó là BCNN phải tìm.

Ta có: \(24 = {2^3}.3;36 = {2^2}{.3^2}\)

Nên \(BCNN\left( {24;36} \right) = {2^3}{.3^2} = 72\).

Dựa vào quy tắc nhân hai số nguyên.

Ta có: (-8).(-125) = 8.125 = 1 000.

a, b) Viết tập hợp bằng cách liệt kê các phần tử.

c) So sánh các số nguyên để sắp xếp.

d) Thực hiện phép tính với số nguyên.

a) Tập hợp A các số tự nhiên là bội của 6 và nhỏ hơn 20 là: A = {0; 6; 12; 18}.

b) Tập hợp B các ước của 10 là: B = Ư(10) = {1; –1; 2; –2; 5; –5; 10; –10}.

c) Các số nguyên âm là: -5; -10. Vì 5 < 10 nên -5 > -10.

Các số nguyên dương là 3; 12. Ta có: 3 < 12.

Vậy các số nguyên theo thứ tự giảm dần là: 12; 3; 0; -5; -10.

d) Nhiệt độ đêm hôm đó ở New York là: – 5 ⁰ C + (–7 ⁰ C) = –12 ⁰

a) Sử dụng tính chất kết hợp của phép nhân và phép cộng số tự nhiên.

b) Sử dụng quy tắc tính với số nguyên.

c) Tìm BC(9;10;12). Tìm bội chung của 9; 10 và 12 trong khoảng 350 đến 450.

a) 173 + 62.173 + 173 = 173.(37 + 62 + 1) = 173.100 = 17300

b) - 3x + 15 = 3 \( \cdot \)( - 5).

- 3x = - 15 – 15

- 3x = - 30

x = –30 : (–3)

x = 10

Vậy x = 10.

c) Gọi số học sinh đi tham quan là x (học sinh) (x \( \in N*\))

Vì số học sinh xếp hàng 9, hàng 10, hàng 12 đều thừa 3 học sinh nên \(\left( {x - 3} \right) \in BC(9;10;12)\). Mà số học sinh trong khoảng từ 350 em đến 450 em nên \(350 \le x \le 450\).

Ta có: \(9 = {3^2};10 = 2.5;12 = {2^2}.3\) nên \(BCNN(9;10;12) = {2^2}{.3^2}.5 = 180\).

\( \Rightarrow BC\left( {9;10;12} \right) = B\left( {180} \right) = \left\{ {180;360;540;...} \right\}\)

Vì \(350 \le x \le 450\) nên x – 3 = 360 suy ra x = 363 (TM).

Vậy số học sinh đi tham quan là 363 học sinh.

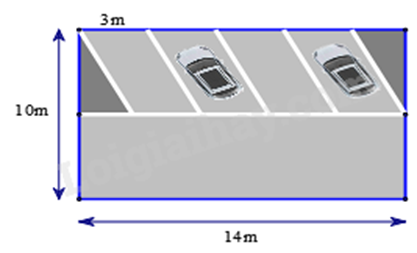
a) Tính diện tích chỗ đậu xe dành cho một ô tô bằng công thức tính diện tích hình bình hành.

b) Diện tích quay đầu xe tính bằng công thức tính diện tích hình chữ nhật.

Diện tích dành cho đậu xe và quay đầu xe = diện tích bốn chỗ đậu xe + diện tích quay đầu xe.

a) Chỗ đậu xe là hình bình hành có chiều cao là: 10:2 = 5 (m).

Diện tích mỗi chỗ đậu xe là: 3.5 = 15 (m ² ).

Vậy diện tích chỗ đậu xe dành cho một ô tô là: 15m ² .

b) Chiều rộng khu vực dành cho quay đầu xe là: 10:2 = 5(m)

Diện tích khu vực dành cho quay đầu xe là: 5.14 = 70(m ² ).

Diện tích dành cho đậu xe và quay đầu xe là: 70 + 15.4 = 130(m ² ).

Vậy diện tích dành cho việc đậu xe và quay đầu xe là 130 m ² .

Dựa vào kiến thức về trục đối xứng: Có một đường thẳng d chia hình thành hai phần mà khi ta “ gấp ” hình theo đường thẳng d thì hai phần đó “ chồng khít ” lên nhau .

Dựa vào kiến thức về tâm đối xứng: Những hình có một điểm O sao cho khi quay nửa vòng quanh điểm O ta được vị trí mới của hình chồng khít với vị trí ban đầu (trước khi quay) thì được gọi là hình có tâm đối xứng và điểm O được gọi là tâm đối xứng của hình.

Hình có trục đối xứng là : hình 1; hình 2; hình 3.

Hình có tâm đối xứng là : hình 3.