Đề thi vào 10 môn Toán Bến Tre năm 2021
Tải vềCâu 1 (1,0 điểm):
Đề bài
Câu 1 (1 ,0 điểm):
|
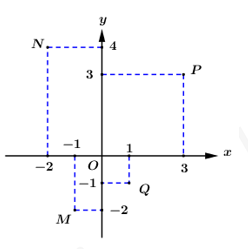
Dựa vào hình vẽ bên, hãy: a) Viết ra tọa độ các điểm \(M\) và \(P\). b) Xác định hoành độ điểm \(N\). c) Xác định tung độ điểm \(Q\). |
Câu 2 (1 ,0 điểm):
a) Tính giá trị của biểu thức \(A = \sqrt {9.32} - \sqrt 2 \).
b) Rút gọn biểu thức \(B = \dfrac{{x - 5}}{{\sqrt x + \sqrt 5 }}\) với \(x \ge 0\).
Câu 3 (1,0 điểm):
Cho đường thẳng \(\left( d \right):y = \left( {5m - 6} \right)x + 2021\) với \(m\) là tham số.
a) Điểm \(O\left( {0;0} \right)\) có thuộc \(\left( d \right)\) không? Vì sao?
b) Tìm các giá trị của \(m\) để \(\left( d \right)\) song song với đường thẳng: \(y = 4x + 5\)
Câu 4 (1,0 điểm):
Vẽ đồ thị hàm số \(y = \dfrac{1}{2}{x^2}\)
Câu 5 (2,5 điểm):
a) Giải phương trình: \(5{x^2} + 6x - 11 = 0\).
b) Giải hệ phương trình: \(\left\{ {\begin{array}{*{20}{c}}{x + y = 5}\\{4x + 5y = 9}\end{array}} \right.\)
c) Gọi \({x_1},\,\,{x_2}\) là hai nghiệm của phương trình: \({x^2} - 2\left( {m - 3} \right)x - 6m - 7 = 0\) với m là tham số. Tìm giá trị nhỏ nhất của biểu thức: \(C = {\left( {{x_1} + {x_2}} \right)^2} + 8{x_1}{x_2}\).
Câu 6 (1,0 điểm):
|
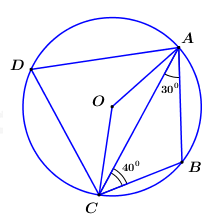
Cho tứ giác \(ABCD\) nội tiếp đường tròn \(\left( O \right)\), biết \(\angle BAC = {30^0}\), \(\angle BCA = {40^0}\) (như hình vẽ bên). Tính số đo các góc \(\angle ABC,\,\,\angle ADC\) và \(\angle AOC\). |
Câu 7 (2,5 điểm):
Cho đường tròn \(\left( {O;3cm} \right)\) và điểm \(M\) sao cho \(OM = 6cm\). Từ điểm \(M\) kẻ hai tiếp tuyến \(MA\) và \(MB\) đến đường tròn \(\left( O \right)\) (\(A\) và \(B\) là các tiếp điểm). Trên đoạn thẳng \(OA\) lấy điểm \(D\) (\(D\) khác \(A\) và \(O\)), dựng đường thẳng vuông góc với \(OA\) tại \(D\) và cắt \(MB\) tại \(E\).
a) Chứng minh tứ giác \(ODEB\) nội tiếp đường tròn.
b) Tứ giác \(ADEM\) là hình gì? Vì sao?
c) Gọi \(K\) là giao điểm của đường thẳng \(MO\) và \(\left( O \right)\) sao cho \(O\) nằm giữa điểm \(M\) và \(K\). Chứng minh tứ giác \(AMBK\) là hình thoi.
Lời giải
Câu 1 (TH):
Phương pháp:
Nhận biết các điểm nằm trên hệ trục tọa độ \(Oxy\) để đọc được tọa độ của các điểm.
Cách giải:
a) Dựa vào hình vẽ ta có: \(M\left( { - 1; - 2} \right)\), \(P\left( {3;3} \right)\).
b) Dựa vào hình vẽ ta có: \(N\left( { - 2;4} \right)\) nên hoành độ điểm \(N\) là \({x_N} = - 2\).
c) Dựa vào hình vẽ ta có: \(Q\left( {1; - 1} \right)\) nên tung độ điểm \(N\) là \({y_Q} = - 1\).
Câu 2 (TH):
Phương pháp:
a) Vận dụng hằng đẳng thức \(\sqrt {{A^2}} = \left| A \right|\) để tính giá trị của biểu thức \(A\).
b) Vận dụng hằng đẳng thức \(A - B = \left( {\sqrt A - \sqrt B } \right)\left( {\sqrt A + \sqrt B } \right)\) để xác định các nhân tử chung, rút gọn biểu thức \(B\).
Cách giải:
a) \(A = \sqrt {9.32} - \sqrt 2 \)
\(\begin{array}{l}A = \sqrt {9.16.2} - \sqrt 2 \\A = 3.4\sqrt 2 - \sqrt 2 \\A = 12\sqrt 2 - \sqrt 2 \\A = 11\sqrt 2 \end{array}\)
b) Với \(x \ge 0\) ta có:
\(B = \dfrac{{x - 5}}{{\sqrt x + \sqrt 5 }} = \dfrac{{\left( {\sqrt x + \sqrt 5 } \right)\left( {\sqrt x - \sqrt 5 } \right)}}{{\sqrt x + \sqrt 5 }} = \sqrt x - \sqrt 5 \).
Vậy với \(x \ge 0\) thì \(B = \sqrt x - \sqrt 5 \).
Câu 3 (VD):
Phương pháp:
a) Thay tọa độ điểm \(O\left( {0;0} \right)\) vào đường thẳng \(\left( d \right)\) để kiểm tra.
b) Vận dụng quan hệ hai đường thẳng song song.
Cách giải
a) Thay \(x = 0\) và \(y = 0\) vào phương trình đường thẳng \(\left( d \right):y = \left( {5m - 6} \right)x + 2021\) ta được:
\(0 = \left( {5m - 6} \right).0 + 2021 \Leftrightarrow 0 = 2021\) (Vô lý)
Vậy \(O\left( {0;0} \right)\) không thuộc đường thẳng \(\left( d \right)\).
b) Đường thẳng \(\left( d \right)\) song song với đường thẳng: \(y = 4x + 5\) \( \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{5m - 6 = 4}\\{2021 \ne 5\,\,\left( {luon\,\,dung} \right)}\end{array}} \right. \Leftrightarrow m = 2\).
Vậy \(m = 2\) thỏa mãn đề bài.
Câu 4 (VD):
Phương pháp:
Lập bảng giá trị để xác định được các điểm mà \(\left( P \right)\) đi qua (thường chọn 3 hoặc 5 điểm thuộc \(\left( P \right)\)).
Cách giải
Parabol \(\left( P \right):\,\,y = \dfrac{1}{2}{x^2}\) có bề lõm hướng lên và nhận \(Oy\) làm trục đối xứng.
Ta có bảng giá trị sau:
|
\(x\) |
\( - 4\) |
\( - 2\) |
\(0\) |
2 |
4 |
|
\(y = \dfrac{1}{2}{x^2}\) |
8 |
2 |
0 |
2 |
8 |
\( \Rightarrow \) Parabol \(\left( P \right):\,\,y = \dfrac{1}{2}{x^2}\) đi qua các điểm \(\left( { - 4;8} \right)\), \(\left( { - 2;2} \right)\), \(\left( {0;0} \right)\), \(\left( {2;2} \right)\), \(\left( {4;8} \right)\).
Đồ thị Parabol \(\left( P \right):\,\,y = \dfrac{1}{2}{x^2}\):

Câu 5 (VD):
Phương pháp:
a) Vận dụng cách nhẩm nghiệm nhanh với phương trinh bậc hai một ẩn: \(a{x^2} + bx + c = 0\left( {a \ne 0} \right)\) nếu \(a + b + c = 0\) thì phương trình có hai nghiệm phân biệt \({x_1} = 1;{x_2} = \dfrac{c}{a}\)
b) Sử dụng phương pháp cộng đại số để giải hệ phương trình.
c) Điều kiện để phương trình có hai nghiệm phân biệt \( \Leftrightarrow \Delta > 0\) (hoặc \(\Delta ' > 0\))
Áp dụng Định lý Vi – ét, xác định được \({x_1} + {x_2}\) và \({x_1}.{x_2}\) sau đó thay vào biểu thức \(C\)
Vận dụng hằng đẳng thức \({\left( {A - B} \right)^2}\) để tìm giá trị nhỏ nhất.
Cách giải
a) Ta có \(a + b + c = 5 + 6 - 11 = 0\) nên phương trình có nghiệm phân biệt \(\left[ \begin{array}{l}{x_1} = 1\\{x_2} = \dfrac{c}{a} = - \dfrac{{11}}{5}\end{array} \right.\).
Vậy phương trình có tập nghiệm \(S = \left\{ {\dfrac{{ - 11}}{5};\,1} \right\}\).
b) \(\left\{ {\begin{array}{*{20}{c}}{x + y = 5}\\{4x + 5y = 9}\end{array}} \right. \Leftrightarrow \left\{ \begin{array}{l}4x + 4y = 20\\4x + 5y = 9\end{array} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{y = - 11}\\{x = 5 - y}\end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{x = 16}\\{y = - 11}\end{array}} \right.} \right.\)
Vậy hệ phương trình có nghiệm \(\left( {x;y} \right) = \left( {16;\, - 11} \right)\).
c) Phương trình \({x^2} - 2\left( {m - 3} \right)x - 6m - 7 = 0\) có \(\Delta ' = {\left( {m - 3} \right)^2} + 6m + 7 = {m^2} + 16 > 0\) với mọi \(m \in \mathbb{R}\).
Suy ra phương trình trên luôn có hai nghiệm phân biệt \({x_1},\,\,{x_2}\).
Theo định lí Vi-et ta có: \(\left\{ {\begin{array}{*{20}{c}}{{x_1} + {x_2} = 2m - 6}\\{{x_1}{x_2} = - 6m - 7}\end{array}} \right.\)
Theo bài ra ta có:
\(C = {\left( {{x_1} + {x_2}} \right)^2} + 8{x_1}{x_2}\)
\(\begin{array}{l} \Rightarrow C = {\left( {2m - 6} \right)^2} + 8\left( { - 6m - 7} \right)\\ \Leftrightarrow C = 4{m^2} - 24m + 36 - 48m - 56\\ \Leftrightarrow C = 4{m^2} - 72m - 20\\ \Leftrightarrow C = 4\left( {{m^2} - 18m + 81} \right) - 4.81 - 20\\ \Leftrightarrow C = 4{\left( {m - 9} \right)^2} - 344\end{array}\)
Vì \({\left( {m - 9} \right)^2} \ge 0\,\,\forall m \Leftrightarrow 4{\left( {m - 9} \right)^2} \ge 0\,\,\forall m \Leftrightarrow 4{\left( {m - 9} \right)^2} - 344 \ge - 344\,\,\forall m\).
Vậy \({C_{\min }} = - 344\). Dấu “=” xảy ra khi và chỉ khi \(m = 9\).
Câu 6 (VD):
Phương pháp:
Vận dụng tính chất: Tổng ba góc trong một tam giác bằng \({180^0}\) và mối quan hệ góc nội tiếp và góc ở tâm của đường tròn.
Cách giải

Xét tam giác \(ABC\) có: \(\angle BAC + \angle BCA + \angle ABC = {180^0}\) (tổng 3 góc trong một tam giác).
\( \Rightarrow {30^0} + {40^0} + \angle ABC = {180^0} \Rightarrow \angle ABC = {110^0}\).
Tứ giác \(ABCD\) nội tiếp đường tròn \(\left( O \right)\) nên \(\angle ABC + \angle ADC = {180^0}\) (tổng hai góc đối diện của tứ giác nội tiếp) \( \Rightarrow \angle {110^0} + \angle ADC = {180^0} \Rightarrow \angle ADC = {70^0}\).
Ta có: \(\angle AOC = 2ADC\) (góc nội tiếp và góc ở tâm cùng chắn cung \(AC\)) \( \Rightarrow \angle AOC = {2.70^0} = {140^0}\).
Vậy \(\angle ABC = {110^0},\,\,\angle ADC = {70^0},\,\,\angle AOC = {140^0}\).
Câu 7 (VDC):
Phương pháp:
a) Áp dụng dấu hiệu nhận biết của tứ giác nội tiếp: Tứ giác có tổng hai góc đối bằng \({180^0}\) là tứ giác nội tiếp.
b) Vận dụng quan hê từ vuông góc đến song song, suy ra \(AM//DE\).
Lại có \(\angle DAM = \angle ADE = {90^0}\), nên \(ADEM\) là hình thang vuông.
c) Gọi \(\left\{ H \right\} = AB \cap OM\).
Vận dụng kiến thức về đường trung trực, hệ thức lượng trong tam giác vuông, mối quan hệ góc – đường tròn
Vận dụng định nghĩa hình thoi để chứng minh \(AMBK\) là hình thoi.
Cách giải
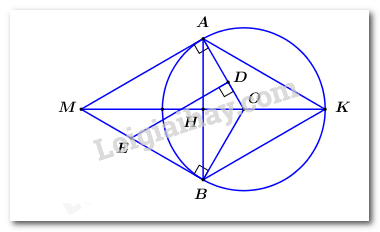
a) Vì \(MA,\,\,MB\) là tiếp tuyến của \(\left( O \right)\) nên \(\angle OAM = \angle OBM = {90^0}\).
Xét tứ giác \(ODEB\) có: \(\angle ODE + \angle OBE = {90^0} + {90^0} = {180^0}\).
\( \Rightarrow ODEB\) là tứ giác nội tiếp (tứ giác có tổng hai góc đối bằng \({180^0}\)).
b) Ta có \(\left\{ \begin{array}{l}AM \bot OA\,\,\left( {gt} \right)\\DE \bot OA\,\,\left( {gt} \right)\end{array} \right.\) \( \Rightarrow AM//DE\) (từ vuông góc đến song song)
\( \Rightarrow ADEM\) là hình thang.
Lại có \(\angle DAM = \angle ADE = {90^0}\) nên \(ADEM\) là hình thang vuông.
c) Gọi \(\left\{ H \right\} = AB \cap OM\).
Ta có: \(OA = OB = 3\,\,cm \Rightarrow O\) thuộc trung trực của \(AB\).
\(MA = MB\) (tính chất 2 tiếp tuyến cắt nhau) \( \Rightarrow M\) thuộc trung trực của \(AB\).
\( \Rightarrow OM\) là trung trực của \(AB\) \( \Rightarrow OM \bot AB\) tại \(H\).
\( \Rightarrow MK\) là trung trực của \(AB\), mà \(M \in MK \Rightarrow MA = MB\).
Xét tam giác \(OAM\) vuông tại \(A\) có đường cao \(AH\), áp dụng hệ thức lượng trong tam giác vuông ta có:
\(OH.OM = O{A^2} \Rightarrow OH = \dfrac{{O{A^2}}}{{OM}} = \dfrac{{{3^2}}}{6} = 1,5\,\,\left( {cm} \right)\).
Xét tam giác vuông \(OAH\) có: \(\sin \angle OAH = \dfrac{{OH}}{{OA}} = \dfrac{{1,5}}{3} = \dfrac{1}{2} \Rightarrow \angle OAH = {30^0}\).
\( \Rightarrow \angle BAM = {90^0} - \angle OAH = {90^0} - {30^0} = {60^0}\).
\( \Rightarrow \Delta MAB\) đều \( \Rightarrow MA = MB = AB\) (1)
Ta lại có: \(\angle AKB = \angle BAM\) (góc nội tiếp và góc tạo bởi tiếp tuyến và dây cung cùng chắn cung \(AB\)).
\( \Rightarrow \angle AKB = {60^0} \Rightarrow \Delta KAB\) đều \( \Rightarrow KA = KB = AB\) (2)
Từ (1) và (2) \( \Rightarrow MA = MB = KA = KB\).
Vậy \(AMBK\) là hình thoi (định nghĩa) (đpcm).