Đề thi vào 10 môn Toán Bình Phước năm 2021 — Không quảng cáo

Đề bài

Câu 1 ( 2,0 điểm):

1. Tính giá trị các biểu thức sau:

\(A = \sqrt {49}  - \sqrt {25} \)                                   \(B = \sqrt 5  + \sqrt {{{\left( {3 - \sqrt 5 } \right)}^2}} \)

2. Cho biểu thức \(P = \dfrac{{x - 4}}{{\sqrt x  + 2}} + \dfrac{{x + 3\sqrt x }}{{\sqrt x }}\) với \(x > 0\).

a. Rút gọn biểu thức \(P\).

b. Tìm giá trị của \(x\) để \(P = 5\).

Câu 2 ( 2,0 điểm):

1. Cho parabol \(\left( P \right):\,\,y = 2{x^2}\) và đường thẳng \(\left( d \right):\,\,y = x + 1\).

a) Vẽ parabol \(\left( P \right)\) và đường thẳng \(d\) trên cùng một hệ trục tọa độ \(Oxy\).

b) Tìm tọa độ giao điểm của \(\left( P \right)\) và \(\left( d \right)\) bằng phép tính.

2. Không sử dụng máy tính cầm tay, giải hệ phương trình: \(\left\{ \begin{array}{l}2x - y = 4\\x + 2y = 7\end{array} \right.\)

Câu 3 (2,5 điểm):

1. Cho phương trình \({x^2} + \left( {m - 2} \right)x - 8 = 0\) (1), với \(m\) là tham số.

a) Giải phương trình (1) khi \(m = 4\).

b) Tìm \(m\) để phương trình có hai nghiệm \({x_1},\,\,{x_2}\) sao cho biểu thức \(Q = \left( {{x_1}^2 - 1} \right)\left( {{x_2}^2 - 1} \right)\) đạt giá trị lớn nhất.

2. Hai ô tô khởi hành cùng một lúc để đi từ địa điểm A đến địa điểm B cách nhau 120 km. Vận tốc ô tô thứ hai lớn hơn vận tốc ô tô thứ nhất là 10 km/h nên ô tô thứ hai đến B trước ô tô thứ nhất 24 phút. Tính vận tốc của mỗi ô tô.

Câu 4 (1 ,0 điểm):

Cho tam giác \(ABC\) vuông tại \(A\) có đường cao \(AH\) và đường trung tuyến \(AM\). Biết \(AB = 9\,\,cm\), \(AC = 12\,\,cm\). Hãy tính \(BC,\,\,AH,\,\,AM\) và diện tích tam giác \(ABM\).

Câu 5 ( 2,5 điểm):

Từ điểm \(A\) nằm ngoài đường tròn \(\left( O \right)\) kẻ hai tiếp tuyến \(AB,\,\,AC\)(\(B,C\) là tiếp điểm). Kẻ cát tuyến \(AEF\) không đi qua tâm (\(E\) nằm giữa \(A\) và \(F\);\(O\) và \(B\) nằm về hai phía so với cát tuyến ). Gọi \(K\)là trung điểm của \(EF\).

a) Chứng minh tứ giác \(OBAC\) nội tiếp đường tròn.

b) Chứng minh \(KA\) là phân giác của \(\angle BKC\).

c) Kẻ dây \(ED\) vuông góc \(OB\) sao cho \(ED\) cắt \(BC\) tại \(M\). Chứng minh \(FM\) đi qua trung điểm \(I\) của đoạn thẳng \(AB\).

Lời giải

Câu 1 (TH)

Phương pháp:

1) Sử dụng hằng đẳng thức: \(\sqrt {{A^2}}  = \left| A \right| = \left\{ \begin{array}{l}A\,\,\,khi\,\,A \ge 0\\ - A\,\,\,khi\,\,A < 0\end{array} \right.\)

Thực hiện các phép tính với căn bậc hai.

2) a) Xác định mẫu thức chung của biểu thức

Quy đồng các phân thức, thực hiện các phép toán từ đó rút gọn được biểu thức.

b) Giải phương trình với \(P = 5\), ta tìm được \(x\), đối chiếu điều kiện và kết luận.

Cách giải:

1)

\(\begin{array}{l}A = \sqrt {49}  - \sqrt {25} \\A = \sqrt {{7^2}}  - \sqrt {{5^2}} \\A = 7 - 5 = 2\end{array}\)

Vậy \(A = 2\).

\(\begin{array}{l}B = \sqrt 5  + \sqrt {{{\left( {3 - \sqrt 5 } \right)}^2}} \\B = \sqrt 5  + \left| {3 - \sqrt 5 } \right|\\B = \sqrt 5  + 3 - \sqrt 5 \,\,\left( {Do\,\,3 - \sqrt 5  > 0} \right)\\B = 3\end{array}\)

Vậy \(B = 3\).

2) a) Với \(x > 0\) ta có:

\(\begin{array}{l}P = \dfrac{{x - 4}}{{\sqrt x  + 2}} + \dfrac{{x + 3\sqrt x }}{{\sqrt x }}\\P = \dfrac{{\left( {\sqrt x  + 2} \right)\left( {\sqrt x  - 2} \right)}}{{\sqrt x  + 2}} + \dfrac{{\sqrt x \left( {\sqrt x  + 3} \right)}}{{\sqrt x }}\\P = \sqrt x  - 2 + \sqrt x  + 3\\P = 2\sqrt x  + 1\end{array}\)

Vậy với \(x > 0\) thì \(P = 2\sqrt x  + 1\).

b) Để \(P = 5\) thì \(2\sqrt x  + 1 = 5 \Leftrightarrow 2\sqrt x  = 4 \Leftrightarrow \sqrt x  = 2 \Leftrightarrow x = 4\,\,\left( {tm} \right)\).

Vậy để \(P = 5\) thì \(x = 4\).

Câu 2 (VD):

Phương pháp:

1) a) Vẽ đồ thị của hàm số \(y = a{x^2}\left( {a \ne 0} \right)\)

+ Nhận xét về hệ số \(a\) và sự biến thiên của hàm số

+ Lập bảng giá trị tương ứng của \(x\) và \(y\)

+ Xác định được các điểm mà đồ thị đi qua, vẽ đồ thị.

Vẽ đồ thị của hàm số \(y = ax + b\)

+ Lập bảng giá trị tương ứng của \(x\) và \(y\)

+ Xác định được các điểm mà đồ thị đi qua, vẽ đồ thị.

b) Xét phương trình hoành độ giao điểm giữa \(\left( P \right)\) và \(\left( d \right)\)

Tính nhẩm nghiệm của phương trình bậc hai: Nếu \(a + b + c = 0\) thì phương trình \(a{x^2} + bx + c = 0\left( {a \ne 0} \right)\) có hai nghiệm phân biệt: \({x_1} = 1;{x_2} = \dfrac{c}{a}\)

Với mỗi \({x_i}\) tìm được ta tìm được \({y_i}\)

Kết luận giao điểm của \(\left( P \right)\) và \(\left( d \right)\) là: \(\left( {{x_i};{y_i}} \right)\)

Cách giải:

1) a) +) Parabol \(\left( P \right):\,\,y = 2{x^2}\) có bề lõm hướng lên và nhận \(Oy\) làm trục đối xứng.

Ta có bảng giá trị sau:

\( \Rightarrow \) Parabol \(\left( P \right):\,\,y = 2{x^2}\) là đường cong đi qua các điểm \(\left( { - 2;8} \right)\), \(\left( { - 1;2} \right)\), \(\left( {0;0} \right)\), \(\left( {1;2} \right)\), \(\left( {2;8} \right)\).

+) Đường thẳng \(\left( d \right):\,\,y = x + 1\)

Ta có bảng giá trị sau:

\( \Rightarrow \) Đường thẳng \(\left( d \right):\,\,y = x + 1\) đi qua các điểm \(\left( {0;1} \right);\,\,\left( { - 1;0} \right)\).

Đồ thị Parabol \(\left( P \right):\,\,y = {x^2}\) và đường thẳng \(\left( d \right):\,\,y = x + 1\) trên cùng một hệ trục tọa độ \(Oxy\):

b) Hoành độ giao điểm của \(\left( P \right)\) và \(\left( d \right)\) là nghiệm của phương trình \(2{x^2} = x + 1 \Leftrightarrow 2{x^2} - x - 1 = 0\).

Ta có \(a + b + c = 2 - 1 - 1 = 0\) nên phương trình có 2 nghiệm phân biệt \(\left[ \begin{array}{l}x = 1\\x = \dfrac{c}{a} =  - \dfrac{1}{2}\end{array} \right.\).

+ Với \(x = 1 \Rightarrow y = 1 + 1 = 2\).

+ Với \(x =  - \dfrac{1}{2} \Rightarrow y =  - \dfrac{1}{2} + 1 = \dfrac{1}{2}\).

Vậy tọa độ giao điểm của \(\left( P \right)\) và \(\left( d \right)\) là \(\left( {1;2} \right)\) và \(\left( { - \dfrac{1}{2};\dfrac{1}{2}} \right)\).

2) Ta có:

\(\left\{ \begin{array}{l}2x - y = 4\\x + 2y = 7\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}4x - 2y = 8\\x + 2y = 7\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}5x = 15\\y = 2x - 4\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 3\\y = 2\end{array} \right.\).

Vậy nghiệm của hệ phương trình là \(\left( {x;y} \right) = \left( {3;2} \right)\).

Câu 3 (VD):

Phương pháp:

1) a) Thay \(m = 4\) phương trình \(\left( 1 \right)\)

Tính \(\Delta  = {b^2} - 4ac\) (hoặc \(\Delta ' = {\left( {b'} \right)^2} - ac\)), sử dụng công thức nghiệm của phương trình bậc hai một ẩn: \({x_{1,2}} = \dfrac{{ - b \pm \sqrt \Delta  }}{{2a}}\) (hoặc \({x_{1,2}} = \dfrac{{ - b' \pm \sqrt {\Delta '} }}{a}\)), tính được nghiệm của phương trình, kết luận.

b) Phương trình \(a{x^2} + bx + c = 0\left( {a \ne 0} \right)\) có hai nghiệm phân biệt \(\Delta  > 0\) (hoặc \(\Delta ' > 0\))

Áp dụng hệ thức Vi – ét, tính được \({x_1} + {x_2};{x_1}.{x_2}\) theo \(m\)

Biến đổi, rút gọn biểu thức \(Q\), sử dụng hằng đẳng thức tìm được giá trị lớn nhất của \(Q\).

2) Gọi vận tốc của ô tô thứ nhất là \(x\,\,\left( {km/h} \right)\) (ĐK: \(x > 0\)).

Tính được vấn tốc của ô tô thứ hai theo \(x\)

Tính được thời gian của ô tô thứ nhất và ô tô thứ hai đi hết quãng đường \(AB\) theo \(x\)

Lập được phương trình, giải phương trình tìm được \(x\), đối chiếu điều kiện và kết luận.

Cách giải:

1) a) Thay \(m = 4\) vào phương trình (1) ta được: \({x^2} + 2x - 8 = 0\)

Ta có: \(\Delta ' = 1 + 8 = 9 = {3^2} > 0\) nên phương trình có hai nghiệm phân biệt: \(\left[ \begin{array}{l}{x_1} =  - 1 + \sqrt 9  = 2\\{x_2} =  - 1 - \sqrt 9  =  - 4\end{array} \right.\)

Vậy phương trình có tập nghiệm \(S = \left\{ { - 4;2} \right\}\).

b) Phương trình (1) có: \(\Delta  = {\left( {m - 2} \right)^2} + 32 > 0\,\,\,\forall m\) nên phương trình (1) luôn có hai nghiệm phân biệt \({x_1},\,\,{x_2}\).

Khi đó theo Vi-ét ta có: \(\left\{ {\begin{array}{*{20}{c}}{{x_1} + {x_2} =  - m + 2}\\{{x_1}.{x_2} =  - 8}\end{array}} \right.\)

Ta có:

\(\begin{array}{l}Q = \left( {{x_1}^2 - 1} \right)\left( {{x_2}^2 - 1} \right)\\\,\,\,\,\, = {x_1}^2{x_2}^2 - \left( {{x_1}^2 + {x_2}^2} \right) + 1\\\,\,\,\, = {x_1}^2{x_2}^2 - {\left( {{x_1} + {x_2}} \right)^2} + 2{x_1}{x_2} + 1\end{array}\)

\( \Rightarrow Q = 64 - {\left( { - m + 2} \right)^2} - 16 + 1 =  - {\left( { - m + 2} \right)^2} + 49 \le 49\,\,\,\forall m\).

Vậy \({Q_{\max }} = 49\). Dấu “=” xảy ra khi \(m = 2\).

Vậy giá trị lớn nhất của Q bằng 49 khi \(m = 2\).

2) Gọi vận tốc của ô tô thứ nhất là \(x\,\,\left( {km/h} \right)\) (ĐK: \(x > 0\)).

Suy ra vận tốc của ô tô thứ hai là \(x + 10\) (km/h)

Thời gian ô tô thứ nhất đi hết quãng đường \(AB\) là: \(\dfrac{{120}}{x}\) (h)

Thời gian ô tô thứ hai đi hết quãng đường \(AB\)  là \(\dfrac{{120}}{{x + 10}}\) (h)

Vì ô tô thứ hai đến B trước ô tô thứ nhất 24 phút = \(\dfrac{2}{5}\) giờ nên ta có phương trình:

\(\begin{array}{l}\,\,\,\,\,\,\dfrac{{120}}{x} - \dfrac{{120}}{{x + 10}} = \dfrac{2}{5}\\ \Leftrightarrow 600\left( {x + 10} \right) - 600x = 2x\left( {x + 10} \right)\\ \Leftrightarrow 600x + 6000 - 600x = 2{x^2} + 20x\\ \Leftrightarrow 2{x^2} + 20x - 6000 = 0\\ \Leftrightarrow {x^2} + 10x - 3000 = 0\end{array}\)

Ta có: \(\Delta ' = {\left( { - 5} \right)^2} + 3000 = 3025 = {55^2} > 0\) nên phương trình có 2 nghiệm phân biệt \(\left[ \begin{array}{l}{x_1} =  - 5 + 55 = 50\,\,\,\,\,\left( {tm} \right)\\{x_2} =  - 5 - 55 =  - 60\,\,\left( {ktm} \right)\end{array} \right.\)

Vậy vận tốc của ô tô thứ nhất là 50 km/h và vận tốc của ô tô thứ hai là 60 km/h.

Câu 4 (VD):

Phương pháp:

Áp dụng định lí Pytago trong tam giác vuông \(ABC\) tính được \(BC\)

Áp dụng hệ thức lượng trong tam giác vuông \(ABC\) tính được \(AH\)

\(AM\) là trung tuyến ứng với cạnh huyền của tam giác vuông \(ABC\) tính được \(BM\)

\({S_{ABM}} = \dfrac{1}{2}AH.BM\)

Cách giải:

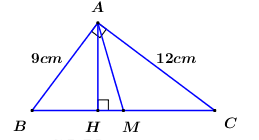
Áp dụng định lí Pytago trong tam giác vuông \(ABC\) ta có:

\(\begin{array}{l}\,\,\,\,\,B{C^2} = A{B^2} + A{C^2}\\ \Rightarrow B{C^2} = {9^2} + {12^2}\\ \Rightarrow B{C^2} = 225\\ \Rightarrow BC = \sqrt {225}  = 15\,\,\left( {cm} \right)\end{array}\)

Áp dụng hệ thức lượng trong tam giác vuông \(ABC\) ta có:

\(AB.AC = AH.BC \Rightarrow AH = \dfrac{{AB.AC}}{{BC}} = \dfrac{{9.12}}{{15}} = 7,2\,\,\left( {cm} \right)\).

Vì \(AM\) là trung tuyến ứng với cạnh huyền của tam giác vuông \(ABC\) nên \(AM = BM = \dfrac{1}{2}BC = \dfrac{1}{2}.15 = 7,5\,\,\left( {cm} \right)\) (định lí đường trung tuyến trong tam giác vuông).

Ta có \({S_{\Delta ABM}} = \dfrac{1}{2}AH.BM = \dfrac{1}{2}.AH.\dfrac{1}{2}BC = \dfrac{1}{4}.7,2.15 = 27\,\,\left( {c{m^2}} \right)\).

Vậy \(BC = 15\,\,cm,\,\,AH = 7,2\,\,cm,\,\,AM = 7,5\,\,cm\), \({S_{\Delta ABM}} = 27\,\,c{m^2}\).

Câu 5 (VDC):

Phương pháp:

a) Vận dụng dấu hiệu nhận biết: Tứ giác có tổng hai góc đối bằng \({180^0}\) là tứ giác nội tiếp.

b) Ta sẽ chứng minh:

c) Gọi \(J\) là giao điểm của \(AK\) và \(BC\)

Gọi I là giao điểm của \(FM\) và \(AB\). Ta sẽ chứng minh \(I\) là trung điểm của \(AB\).

Cách giải:

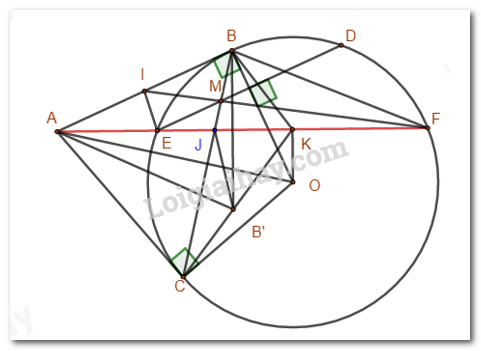
a) Ta có: \(AB,AC\) là tiếp tuyến của đường tròn nên \(\left\{ \begin{array}{l}OA \bot AB\\OC \bot AC\end{array} \right. \Rightarrow \left\{ \begin{array}{l}\angle ABO = {90^0}\\\angle ACO = {90^0}\end{array} \right. \Rightarrow \angle ABO + \angle ACO = {180^0}\)

\( \Rightarrow OBAC\) là tứ giác nội tiếp đường tròn đường kính \(AO\) (dhnb).

b) Vì \(AB,AC\) là tiếp tuyến của đường tròn nên \(AB = AC\) (tính chất hai tiếp tuyến cắt nhau).

Ta có \(K\) là trung điểm của \(EF\) nên \(OK \bot AK\) (quan hệ vuông góc giữa đường kính và dây cung).

\( \Rightarrow \angle OKA = {90^0}\) \( \Rightarrow K\) thuộc đường tròn đường kính \(AO\) hay 5 điểm \(O,\,\,K,\,\,B,\,\,A,\,\,C\) cùng thuộc một đường tròn.

(góc chắn hai cung bằng nhau)

Vậy \(KA\) là phân giác của \(\angle BKC\).

c) Gọi \(J\) là giao điểm của \(AK\) và \(BC\)

Gọi I là giao điểm của \(FM\) và \(AB\). Ta sẽ chứng minh \(I\) là trung điểm của \(AB\).

Xét tam giác \(ABJ\) và \(AKB\) ta có:

\(\angle BAK\) chung

\(\angle ABJ = \angle BKA\,\,\left( { = \angle ACB} \right)\)

\( \Rightarrow \Delta ABJ\) đồng dạng với \(\Delta AKB\) (g.g) \( \Rightarrow \dfrac{{AJ}}{{AB}} = \dfrac{{AB}}{{AK}}\) (cặp cạnh tương ứng) \( \Rightarrow A{B^2} = AJ.AK\)

Tương tự ta có: \(\Delta ABE\) đồng dạng với \(\Delta AFB\) (g.g) \( \Rightarrow \dfrac{{AB}}{{AF}} = \dfrac{{AE}}{{AB}} \Rightarrow A{B^2} = AE.AF\)

\( \Rightarrow AJ.AK = AE.AF \Rightarrow \dfrac{{AF}}{{AJ}} = \dfrac{{AK}}{{AE}} = \dfrac{{AF - AK}}{{AJ - AE}} = \dfrac{{FK}}{{EJ}} = \dfrac{{EK}}{{EJ}}\) (Vì \(K\) là trung điểm của \(EF\)) \( \Rightarrow \dfrac{{AF}}{{EK}} = \dfrac{{AJ}}{{EJ}}\).

Ta lại có: \(\left\{ \begin{array}{l}EM \bot OB\,\,\left( {gt} \right)\\OB \bot AB\,\,\,\left( {gt} \right)\end{array} \right. \Rightarrow EM//AB \Rightarrow \left\{ \begin{array}{l}\dfrac{{AB}}{{EM}} = \dfrac{{AJ}}{{EJ}}\\\dfrac{{AI}}{{EM}} = \dfrac{{AF}}{{EF}}\end{array} \right.\) (Định lí Ta-lét)

\( \Rightarrow \dfrac{{AI}}{{EM}} = \dfrac{{AF}}{{2EK}} = \dfrac{1}{2}.\dfrac{{AJ}}{{EJ}} = \dfrac{1}{2}.\dfrac{{AB}}{{EM}} \Rightarrow AI = \dfrac{{AB}}{2}\).

Vậy \(I\) là trung điểm của \(AB\) (đpcm).