Đề thi vào 10 môn Toán Bình Thuận năm 2020
Tải vềBài 1: Rút gọn biểu thức
Đề bài
Bài 1: Rút gọn biểu thức \(A = \left( {\sqrt 6 + \sqrt 3 } \right).\sqrt 3 - 3\sqrt 2 .\)
Bài 2: Giải phương trình và hệ phương trình sau:
a) \({x^2} + 2x - 3 = 0\) b) \(\left\{ \begin{array}{l}x + y = 7\\2x - y = 5\end{array} \right.\)
Bài 3:
a) Vẽ đồ của thị hàm số \(y = {x^2}\) trên mặt phẳng tọa độ \(Oxy\).
b) Cho hàm số \(y = mx + n\) có đồ thị là \(\left( d \right)\). Tìm giá trị của \(m\) và \(n\) biết \(\left( d \right)\) song song với đường thẳng \(\left( {d'} \right):\,\,y = x + 3\) và đi qua điểm \(M\left( {2;4} \right)\).
Bài 4: Lớp 9A có 80 quyển vở dự định khen thưởng học sinh giỏi cuối năm. Thực tế cuối năm tăng thêm 2 học sinh giỏi, nên mỗi phần thưởng giảm đi 2 quyển vở so với dự định. Hỏi cuối năm lớp 9A có bao nhiêu học sinh giỏi, biết mỗi phần thưởng có số quyển vở bằng nhau.
Bài 5:
Cho nửa đường tròn \(\left( O \right)\) đường kính \(AB = 2R\). Trên đoạn thẳng \(OB\) lấy điểm \(M\) (\(M\) khác \(O\) và \(B\)). Trên nửa đường tròn \(\left( O \right)\) lấy điểm \(N\) (\(N\) khác \(A\) và \(B\)). Đường thẳng vuông góc với \(MN\) tại \(N\) cắt các tiếp tuyến \(Ax,\,\,By\) của nửa đường tròn \(\left( O \right)\) lần lượt tại \(C\) và \(D\) (\(Ax,\,\,By\) và nửa đường tròn cùng thuộc một nửa mặt phẳng bờ \(AB\)).
a) Chứng minh tứ giác \(ACNM\) nội tiếp.
b) Chứng minh \(AN.MD = NB.CM\).
c) Gọi \(E\) là giao điểm của \(AN\) và \(CM\). Đường thẳng qua \(E\) và vuông góc với \(BD\) cắt \(MD\) tại \(F\). Chứng minh \(N,\,\,F,\,\,B\) thẳng hàng.
Lời giải
Bài 1 (1 điểm):
Cách giải:
Rút gọn biểu thức \(A = \left( {\sqrt 6 + \sqrt 3 } \right).\sqrt 3 - 3\sqrt 2 .\)
\(\begin{array}{l}A = \left( {\sqrt 6 + \sqrt 3 } \right).\sqrt 3 - 3\sqrt 2 \\\,\,\,\,\, = \sqrt 6 .\sqrt 3 + \sqrt 3 .\sqrt 3 - 3\sqrt 2 \\\,\,\,\,\, = \sqrt {18} + 3 - 3\sqrt 2 \\\,\,\,\,\, = 3\sqrt 2 + 3 - 3\sqrt 2 \\\,\,\,\,\, = 3.\end{array}\)
Vậy \(A = 3.\)
Bài 2 (2 điểm):
Cách giải:
Giải phương trình và hệ phương trình sau:
a) \({x^2} + 2x - 3 = 0\)
Phương trình có: \(a + b + c = 1 + 2 - 3 = 0\)
\( \Rightarrow \) Phương trình có hai nghiệm phân biệt: \(\left[ \begin{array}{l}{x_1} = 1\\{x_2} = \dfrac{c}{a} = - 3\end{array} \right..\)
Vậy phương trình có tập nghiệm \(S = \left\{ {1; - 3} \right\}.\)
b) \(\left\{ \begin{array}{l}x + y = 7\\2x - y = 5\end{array} \right.\) \( \Leftrightarrow \left\{ \begin{array}{l}3x = 12\\y = 7 - x\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 4\\y = 7 - 4 = 3\end{array} \right..\)
Vậy hệ phương trình có nghiệm duy nhất: \(\left( {x;\,\,y} \right) = \left( {4;\,\,3} \right).\)
Bài 3 (2,0 điểm)
Cách giải:
a) Vẽ đồ của thị hàm số \(y = {x^2}\) trên mặt phẳng tọa độ \(Oxy\) .
Ta có bảng giá trị:
|
\(x\) |
\( - 2\) |
\( - 1\) |
0 |
1 |
2 |
|
\(y = {x^2}\) |
4 |
1 |
0 |
1 |
4 |
Do đó, đồ thị hàm số \(y = {x^2}\) là đường cong đi qua các điểm \(\left( { - 2;4} \right)\), \(\left( { - 1;1} \right)\), \(\left( {0;0} \right)\), \(\left( {1;1} \right)\), \(\left( {2;4} \right)\) và nhận \(Oy\) làm trục đối xứng.
Đồ thị hàm số:
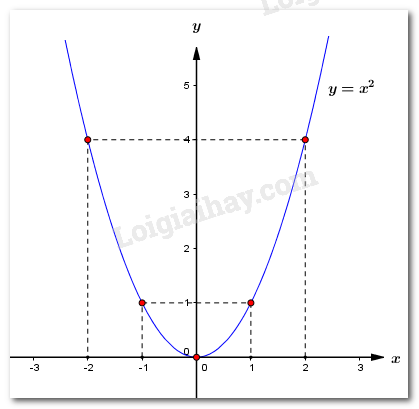
b) Cho hàm số \(y = mx + n\) có đồ thị là \(\left( d \right)\) . Tìm giá trị của \(m\) và \(n\) biết \(\left( d \right)\) song song với đường thẳng \(\left( {d'} \right):\,\,y = x + 3\) và đi qua điểm \(M\left( {2;4} \right)\) .
Vì đường thẳn \(\left( d \right)\) song song với đường thẳng \(\left( {d'} \right):\,\,y = x + 3\) nên ta có: \(\left\{ \begin{array}{l}m = 1\\n \ne 3\end{array} \right.\).
Khi đó phương trình đường thẳng \(\left( d \right)\) có dạng \(y = x + n\) (với \(n \ne 3\))
Mà \(M\left( {2;4} \right) \in d \Rightarrow 4 = 2 + n \Leftrightarrow n = 2\,\,\left( {tm} \right)\).
Vậy \(m = 1,\,\,n = 2\).
Bài 4 (1 điểm):
Cách giải:
Lớp 9A có 80 quyển vở dự định khen thưởng học sinh giỏi cuối năm. Thực tế cuối năm tăng thêm 2 học sinh giỏi, nên mỗi phần thưởng giảm đi 2 quyển vở so với dự định. Hỏi cuối năm lớp 9A có bao nhiêu học sinh giỏi, biết mỗi phần thưởng có số quyển vở bằng nhau.
Gọi số học sinh giỏi lớp 9A theo dự định là \(x\) (học sinh) \(\left( {x \in {\mathbb{N}^*}} \right).\)
\( \Rightarrow \) Dự định, mỗi phần thưởng có số quyển vở là: \(\dfrac{{80}}{x}\) (quyển vở).
Số học sinh giỏi thực tế của lớp 9A là: \(x + 2\) (học sinh).
\( \Rightarrow \) Thực tế, mỗi phần thưởng có số quyển vở là: \(\dfrac{{80}}{{x + 2}}\) (quyển vở).
Thực tế, mỗi mỗi phần thưởng giảm đi 2 quyển vở so với dự định nên ta có phương trình:
\(\begin{array}{l}\,\,\,\,\,\,\,\dfrac{{80}}{x} - \dfrac{{80}}{{x + 2}} = 2\\ \Leftrightarrow 80\left( {x + 2} \right) - 80x = 2x\left( {x + 2} \right)\\ \Leftrightarrow 80x + 160 - 80x = 2{x^2} + 4x\\ \Leftrightarrow 2{x^2} + 4x - 160 = 0\\ \Leftrightarrow {x^2} + 2x - 80 = 0\\ \Leftrightarrow {x^2} + 10x - 8x - 80 = 0\\ \Leftrightarrow x\left( {x + 10} \right) - 8\left( {x + 10} \right) = 0\\ \Leftrightarrow \left( {x - 8} \right)\left( {x + 10} \right) = 0\\ \Leftrightarrow \left[ \begin{array}{l}x - 8 = 0\\x + 10 = 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = 8\,\,\,\left( {tm} \right)\\x = - 10\,\,\,\left( {ktm} \right)\end{array} \right.\end{array}\)
Vậy cuối năm lớp 9A có \(8 + 2 = 10\) học sinh giỏi.
Bài 5 (4,0 điểm)
Cách giải:
Cho nửa đường tròn \(\left( O \right)\) đường kính \(AB = 2R\) . Trên đoạn thẳng \(OB\) lấy điểm \(M\) ( \(M\) khác \(O\) và \(B\) ). Trên nửa đường tròn \(\left( O \right)\) lấy điểm \(N\) ( \(N\) khác \(A\) và \(B\) ). Đường thẳng vuông góc với \(MN\) tại \(N\) cắt các tiếp tuyến \(Ax,\,\,By\) của nửa đường tròn \(\left( O \right)\) lần lượt tại \(C\) và \(D\) ( \(Ax,\,\,By\) và nửa đường tròn cùng thuộc một nửa mặt phẳng bờ \(AB\) ).

a) Chứng minh tứ giác \(ACNM\) nội tiếp.
Vì \(AC\) là tiếp tuyến của \(\left( O \right)\) tại \(A\) nên \(\angle MAC = {90^0}\).
Vì \(MN \bot CD\) tại \(N\) nên \(\angle MNC = \angle MND = {90^0}\).
Xét tứ giác \(ACNM\) có \(\angle MAC + \angle MNC = {90^0} + {90^0} = {180^0}\).
\( \Rightarrow ACNM\) là tứ giác nội tiếp (tứ giác có tổng hai góc đối bằng \({180^0}\)) (đpcm).
b) Chứng minh \(AN.MD = NB.CM\) .
Vì \(BD\) là tiếp tuyến của \(\left( O \right)\) tại \(B\) nên \(\angle MBD = {90^0}\).
Xét tứ giác \(BMND\) có: \(\angle MBD + \angle MND = {90^0} + {90^0} = {180^0}\).
\( \Rightarrow BMND\) là tứ giác nội tiếp (tứ giác có tổng hai góc đối bằng \({180^0}\)).
\( \Rightarrow \angle MDN = \angle MBN\) (hai góc nội tiếp cùng chắn cung \(MN\)) \( \Rightarrow \angle ABN = \angle MDC\).
Vì \(ACNM\) là tứ giác nội tiếp (theo câu a).
\( \Rightarrow \angle MAN = \angle MCN\) (hai góc nội tiếp cùng chắn cung \(MN\)) \( \Rightarrow \angle BAN = \angle MCD\).
Xét \(\Delta ABN\) và \(\Delta CDN\) có:
\(\begin{array}{l}\angle ABN = \angle MDC\,\,\left( {cmt} \right)\\\angle BAN = \angle MCD\,\,\left( {cmt} \right)\\ \Rightarrow \Delta ABN \sim \Delta CDM\,\,\left( {g.g} \right)\end{array}\)
\( \Rightarrow \dfrac{{AN}}{{CM}} = \dfrac{{NB}}{{MD}}\) (hai cạnh tương ứng) \( \Rightarrow AN.MD = NB.CM\) (đpcm).
c) Gọi \(E\) là giao điểm của \(AN\) và \(CM\) . Đường thẳng qua \(E\) và vuông góc với \(BD\) cắt \(MD\) tại \(F\) . Chứng minh \(N,\,\,F,\,\,B\) thẳng hàng.
Gọi \(E = BN \cap DM\), ta chứng minh \(EF \bot BD\).
Vì \(\Delta ABN \sim \Delta CDM\,\,\left( {cmt} \right)\) nên \(\angle ANB = \angle CMD\). Mà \(\angle ANB = {90^0}\) (góc nội tiếp chắn nửa đường tròn) \( \Rightarrow \angle CMD = {90^0}\)
\( \Rightarrow \angle ENF = \angle EMF = {90^0}\).
Xét tứ giác \(MENF\) có: \(\angle ENF + \angle EMF = {90^0} + {90^0} = {180^0}\).
\( \Rightarrow MENF\) là tứ giác nội tiếp (Tứ giác có tổng hai góc đối bằng \({180^0}\)).
\( \Rightarrow \angle {N_1} = \angle {E_1}\) (hai góc nội tiếp cùng chắn cung \(MF\)).
Mà \(\angle {N_1} = \angle {D_1}\) (hai góc nội tiếp cùng chắn cung \(BM\))
\( \Rightarrow \angle {E_1} = \angle {D_1}\) (1).
Vì \(\Delta BDM\) vuông tại \(B\) nên \(\angle {D_1} + \angle BMD = {90^0}\) (hai góc nhọn trong tam giác vuông phụ nhau).
Mà \(\angle BMD + \angle CMD + \angle {M_1} = {180^0}\) \( \Rightarrow \angle {M_1} + \angle BMD = {180^0} - \angle CMD = {180^0} - {90^0} = {90^0}\).
\( \Rightarrow \angle {D_1} = \angle {M_1}\) (2).
Từ (1) và (2) \( \Rightarrow \angle {E_1} = \angle {M_1}\).
Mà hai góc này ở vị trí hai góc so le trong bằng nhau nên \(EF//AM\) hay \(EF//AB\).
Lại có \(AB \bot BD\,\,\left( {gt} \right)\) \( \Rightarrow EF \bot BD\).
Vậy đường thẳng qua \(E\) vuông góc với \(BD\) cắt \(MD\) tại \(F\) thuộc \(BN\) (đpcm).
d) Khi \(\angle ABN = {60^0}\), tính theo \(R\) diện tích của phần nửa hình tròn tâm \(O\), bán kính \(R\) nằm ngoài \(\Delta ABN\).
Xét tam giác vuông \(ABN\) vuông tại \(N\) có \(AB = 2R,\,\,\angle ABN = {60^0}\,\,\left( {gt} \right)\) ta có:
\(AN = AB.\sin \angle ABN = 2R.\sin {60^0} = R\sqrt 3 \).
\(BN = AB.\cos \angle ABN = 2R.\cos {60^0} = R\).
\( \Rightarrow {S_{\Delta ABN}} = \dfrac{1}{2}AN.BN = \dfrac{1}{2}.R\sqrt 3 .R = \dfrac{{{R^2}\sqrt 3 }}{2}\).
Diện tích nửa hình tròn tâm \(\left( {O;R} \right)\) là \({S_T} = \dfrac{1}{2}\pi {R^2}\).
Vậy diện tích của phần nửa hình tròn tâm \(O\), bán kính \(R\) nằm ngoài \(\Delta ABN\) là;
\(S = {S_T} - {S_{\Delta ABN}} = \dfrac{1}{2}\pi {R^2} - \dfrac{{{R^2}\sqrt 3 }}{2} = \dfrac{{{R^2}}}{2}\left( {\pi - \sqrt 3 } \right)\).