Đề thi vào 10 môn Toán Đồng Tháp năm 2020 — Không quảng cáo

Đề bài

Câu 1:

1. Tính giá trị biểu thức $F = \sqrt {49}  + \sqrt {25}$.

2. Tìm điều kiện của x để biểu thức $H = \sqrt {x - 1}$ có nghĩa.

Câu 2:

1. Hàm số $y = 3x + 2$ là hàm số đồng biến hay nghịch biến trên $\mathbb{R}$? Vì sao?

2. Cho parabol $\left( P \right):\,\,y = 2{x^2}$. Điểm $M\left( {2;8} \right)$ có thuộc $\left( P \right)$ hay không? Vì sao?

Câu 3:

1. Giải hệ phương trình $\left\{ \begin{array}{l}2x - y = 3\\x + y = 3\end{array} \right.$.

2. Nhà bạn Lan cách trường học 5km, nhà bạn Mai cách trường học 4km. Mai bắt đầu đi học sớm hơn Lan 5 phút và hai bạn gặp nhau tại cổng trường lúc 6 giờ 50 phút sáng. Biết rằng vận tốc đi xe của bạn Lan lớn hơn vận tốc đi xe của bạn Mai 8km/h. Hỏi Mai bắt đầu đi học lúc mấy giờ.

Câu 4:

Một hộp sữa Ông Thọ là một hình trụ có chiều cao 8cm và bán kính đường tròn đáy là 3,8cm. Tính thể tích hộp sữa (lấy $\pi  \approx 3,14$; kết quả làm tròn đến chữ số thập phân thứ hai).

Câu 5:

Tính chiều rộng AB của một dòng song (hình vẽ). Biết rằng $BC = 9m,\,\,BD = 12m$.

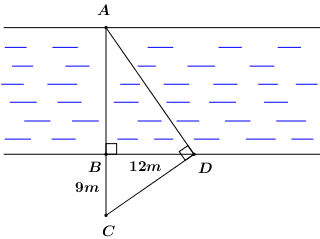
Câu 6:

Cho đường tròn $\left( O \right)$ và một điểm $A$ nằm ngoài $\left( O \right).$ Vẽ các tiếp tuyến $AM,\,\,AN$ với $\left( O \right)$ (với $M,\,\,N$ là các tiếp điểm).

1. Chứng minh tứ giác $AMON$ là tứ giác nội tiếp.

2. Biết $OA = 10\,cm$ và $\angle MAN = {60^0}.$ Tính phần diện tích của tứ giác $AMON$ nằm bên ngoài đường tròn $\left( O \right).$

Lời giải

Câu 1. (2,0 điểm)

Cách giải:

1. Tính giá trị biểu thức $F = \sqrt {49}  + \sqrt {25}$ .

Ta có:

$\begin{array}{l}F = \sqrt {49}  + \sqrt {25} \\F = \sqrt {{7^2}}  + \sqrt {{5^2}} \\F = 7 + 5\\F = 12\end{array}$

Vậy $F = 12$.

2. Tìm điều kiện của x để biểu thức $H = \sqrt {x - 1}$ có nghĩa.

Biểu thức $H = \sqrt {x - 1}$ có nghĩa $\Leftrightarrow x - 1 \ge 0 \Leftrightarrow x \ge 1.$

Vậy biểu thức $H = \sqrt {x - 1}$ có nghĩa khi và chỉ khi $x \ge 1$.

Câu 2. (2,0 điểm)

Cách giải:

1. Hàm số $y = 3x + 2$ là hàm số đồng biến hay nghịch biến trên $\mathbb{R}$ ? Vì sao?

Hàm số $y = 3x + 2$ là hàm số đồng biến trên $\mathbb{R}$ vì đây là hàm số bậc nhất có hệ số $a = 3 > 0$.

2. Cho parabol $\left( P \right):\,\,y = 2{x^2}$ . Điểm $M\left( {2;8} \right)$ có thuộc $\left( P \right)$ hay không? Vì sao?

Thay tọa độ điểm $M\left( {2;8} \right)$ vào hàm số $y = 2{x^2}$ ta có: $8 = {2.2^2} \Leftrightarrow 8 = 8$ (luôn đúng).

Vậy $M\left( {2;8} \right) \in \left( P \right)$.

Câu 3. (2,0 điểm)

Cách giải:

1. Giải hệ phương trình $\left\{ \begin{array}{l}2x - y = 3\\x + y = 3\end{array} \right.$ .

$\left\{ \begin{array}{l}2x - y = 3\\x + y = 3\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}3x = 6\\y = 3 - x\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 2\\y = 3 - 2\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 2\\y = 1\end{array} \right.$.

Vậy hệ phương trình có nghiệm duy nhất $\left( {x;y} \right) = \left( {2;1} \right)$.

2. Nhà bạn Lan cách trường học 5km, nhà bạn Mai cách trường học 4km. Mai bắt đầu đi học sớm hơn Lan 5 phút và hai bạn gặp nhau tại cổng trường lúc 6 giờ 50 phút sáng. Biết rằng vận tốc đi xe của bạn Lan lớn hơn vận tốc đi xe của bạn Mai 8km/h. Hỏi Mai bắt đầu đi học lúc mấy giờ.

Gọi thời gian bạn Mai đi từ nhà đến trường là $x\,\,\left( h \right)$ (ĐK: $x > \dfrac{1}{{12}}$).

Vì Mai bắt đầu đi học sớm hơn Lan 5 phút và hai bạn gặp nhau cùng lúc nên thời gian Mai đi nhà đến trường nhiều hơn thời gian Lan đi từ nhà đến trường là 5 phút = $\dfrac{5}{{60}} = \dfrac{1}{{12}}$ (h) nên thời gian Lan đi từ nhà đến trường là: $x - \dfrac{1}{{12}}\,\,\left( h \right)$.

$\Rightarrow$ Vận tốc xe của bạn Mai là: $\dfrac{4}{x}\,\,\left( {km/h} \right)$.

Vận tốc xe của bạn Lan là: $\dfrac{5}{{x - \dfrac{1}{{12}}}} = \dfrac{{60}}{{12x - 1}}\,\,\left( {km/h} \right)$.

Vì vận tốc đi xe của bạn Lan lớn hơn vận tốc đi xe của bạn Mai 8km/h nên ta có phương trình

$\begin{array}{l}\,\,\,\,\,\,\dfrac{{60}}{{12x - 1}} - \dfrac{4}{x} = 8\\ \Leftrightarrow \dfrac{{15}}{{12x - 1}} - \dfrac{1}{x} = 2\\ \Leftrightarrow 15x - \left( {12x - 1} \right) = 2x\left( {12x - 1} \right)\\ \Leftrightarrow 15x - 12x + 1 = 24{x^2} - 2x\\ \Leftrightarrow 24{x^2} - 5x - 1 = 0\\ \Leftrightarrow 24{x^2} - 8x + 3x - 1 = 0\\ \Leftrightarrow 8x\left( {3x - 1} \right) + \left( {3x - 1} \right) = 0\\ \Leftrightarrow \left( {3x - 1} \right)\left( {8x + 1} \right) = 0\\ \Leftrightarrow \left[ \begin{array}{l}3x - 1 = 0\\8x + 1 = 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = \dfrac{1}{3}\,\,\,\,\,\,\left( {tm} \right)\\x =  - \dfrac{1}{8}\,\,\left( {ktm} \right)\end{array} \right.\end{array}$

$\Rightarrow$ Thời gian bạn Mai đi từ nhà đến trường là $\dfrac{1}{3}h = 20$ phút.

Vậy Mai bắt đầu đi học lúc 6 giờ 50 phút – 20 phút = 6 giờ 30 phút.

Câu 4. (1,0 điểm)

Cách giải:

Một hộp sữa Ông Thọ là một hình trụ có chiều cao 8cm và bán kính đường tròn đáy là 3,8cm. Tính thể tích hộp sữa (lấy $\pi  \approx 3,14$ ; kết quả làm tròn đến chữ số thập phân thứ hai).

Một sữa Ông Thọ có chiều cao $h = 8cm$, bán kính đường tròn đáy $r = 3,8cm$.

Thể tích hộp sữa là; $V = \pi {r^2}h \approx 3,14.3,{8^2}.8 \approx 362,73\,\,\left( {c{m^3}} \right)$.

Vậy thể tích hộp sữa xấp xỉ $362,73\,\,c{m^3}$.

Câu 5. (1,0 điểm)

Cách giải:

Tính chiều rộng AB của một dòng song (hình vẽ). Biết rằng $BC = 9m,\,\,BD = 12m$ .

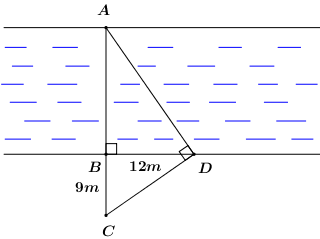
Xét tam giác $ACD$ vuông tại $D$ có đường cao $DB$ ta có:

$D{B^2} = AB.BC$ (hệ thức lượng trong tam giác vuông)

$\Rightarrow {12^2} = AB.9 \Leftrightarrow AB = \dfrac{{{{12}^2}}}{9} = 16\,\,\,\left( m \right)$.

Vậy chiều rộng của dòng sông là $AB = 16m$.

Câu 6. (2 điểm)

Cách giải:

Cho đường tròn $\left( O \right)$ và một điểm $A$ nằm ngoài $\left( O \right).$ Vẽ các tiếp tuyến $AM,\,\,AN$ với $\left( O \right)$ (với $M,\,\,N$ là các tiếp điểm).

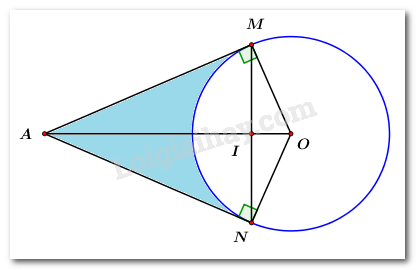
1. Chứng minh tứ giác $AMON$ là tứ giác nội tiếp.

Ta có:$AM,\,\,AN$ là các tiếp tuyến tại $M,\,\,N$ của $\left( O \right)$ $\Rightarrow \left\{ \begin{array}{l}OM \bot AM\\ON \bot AN\end{array} \right.$

$\Rightarrow \angle AMO = \angle ANO = {90^0}$

Xét tứ giác $AMON$ ta có:

$\angle AMO + ANO = {90^0} + {90^0} = {180^0}$

Mà hai góc này là hai góc đối diện

$\Rightarrow AMON$ là tứ giác nội tiếp. (dhnb) (đpcm)

2. Biết $OA = 10\,cm$ và $\angle MAN = {60^0}.$ Tính phần diện tích của tứ giác $AMON$ nằm bên ngoài đường tròn $\left( O \right).$

Ta có: $AM,\,\,AN$ là hai tiếp tuyến cắt nhau tại $A$

$\Rightarrow AO$ là phân giác của $\angle MAN$ (tính chất hai tiếp tuyến cắt nhau).

$\angle MAO = \dfrac{1}{2}\angle MAN = {30^0}$

Xét $\Delta AMO$ vuông tại $M$ ta có:

$\begin{array}{l}AM = AO.\cos \angle MAO = 10.\cos {30^0} = 5\sqrt 3 \,\,cm.\\OM = R = AO.\sin \angle MAO = 10.\sin {30^0} = 5\,cm.\end{array}$

$\begin{array}{l} \Rightarrow {S_{AMO}} = \dfrac{1}{2}OM.AM = \dfrac{1}{2}.5.5\sqrt 3  = \dfrac{{25\sqrt 3 }}{2}\,\,\,c{m^2}\\ \Rightarrow {S_{AMON}} = 2.{S_{AMO}} = 2.\dfrac{{25\sqrt 3 }}{2} = 25\sqrt 3 \,\,c{m^2}.\end{array}$

Ta có: $AMON$ là tứ giác nội tiếp (cmt)

$\Rightarrow \angle MAN + \angle MON = {180^0}$ (tính chất tứ giác nội tiếp)

$\Rightarrow \angle MON = {180^0} - \angle MAN = {180^0} - {60^0} = {120^0}.$

Mà $\angle MON$ là góc ở tâm chắn cung $MN$ $\Rightarrow cung\,\,MN = {120^0}.$

$\Rightarrow$ Diện tích hình quạt $MON$ là: ${S_0} = \dfrac{{\pi {R^2}n}}{{360}} = \dfrac{{\pi {{.5}^2}.120}}{{360}} = \dfrac{{25\pi }}{3}\,\,c{m^2}.$

$\Rightarrow$ Diện tích của phần tứ giác $AMON$ nằm phía ngoài đường tròn $\left( O \right)$ là:

$S = {S_{AMON}} - {S_0} = 25\sqrt 3  - \dfrac{{25\pi }}{3}\,\,\,\left( {c{m^2}} \right).$

Vậy diện tích phần hình cần tính là: $25\sqrt 3  - \dfrac{{25\pi }}{3}\,\,c{m^2}.$