Đề thi vào 10 môn Toán Đồng Nai 2023 có đáp án và lời giải chi tiết — Không quảng cáo

Đề bài

Câu 1: 1) Giải phương trình ${x^2} + 8x + 15 = 0$.

2) Giải phương trình ${x^4} - 3{x^2} - 4 = 0$.

3) Giải hệ phương trình $\left\{ {\begin{array}{*{20}{l}}{2x + 3y = 13}\\{x - 3y = 2}\end{array}} \right.$.

Câu 2: Rút gọn biểu thức $A = \sqrt {{{\left( {\sqrt 2 {\rm{ \;}} - 1} \right)}^2}} {\rm{ \;}} - \frac{1}{3}\sqrt {18}$.

Câu 3: 1) Vẽ đồ thị hàm số $y = {\rm{ \;}} - 2{x^2}$.

2) Tìm tham số thực $m$ để đồ thị hàm số $y = {\rm{ \;}} - 2{x^2}$ và đường thẳng $y = x - m$ có điểm chung.

3) Cho phương trình $3{x^2} + 5x - 1 = 0$ có hai nghiệm ${x_1},{x_2}.$Tính giá trị biểu thức $T = 6{x_1} - 7{x_1}{x_2} + 6{x_2}$.

Câu 4: 1) Hai vòi nước cùng chảy vào một bể cạn (không có nước) sau 40 phút thì đầy bể. Nếu mở vòi thứ nhất chảy trong 15 phút rồi khóa lại, sau đó mở vòi thứ hai chảy tiếp trong 20 phút thì lúc này lượng nước trong bể chiếm $\frac{5}{{12}}$ thể tích của bể nước. Hỏi nếu mở riêng từng vời thì thời gian để mỗi vòi chảy đầy bể là bao lâu?

2) Một hình nón có bán kính đáy $r = 6cm$, độ dài đường sinh $l = 10cm$. Tính thể tích của hình nón đó.

Câu 5: Cho tam giác  ABC  vuông tại  A, trên cạnh  AB  lấy điểm  M (M  khác  A, M  khác  B). Từ điểm  M vẽ đường thẳng  MN  vuông góc với  BC (N  thuộc  BC) , đường thẳng  MN  cắt đường thằng  AC  tại  K .

1) Chứng minh tứ giác AMNC  nội tiếp.

2) Chứng minh $\angle ABK = \angle ACM$.

3) Đoạn thẳng  BK  cắt đường tròn đường kính  BM  tại điểm D (D khác  B). Gọi I là tâm và $r$ là bán kính của đường tròn nội tiếp tam giác BKC . Chứng minh $\frac{1}{r} = \frac{1}{{KN}} + \frac{1}{{CD}} + \frac{1}{{AB}}$.

----- HẾT -----

Lời giải chi tiết

Câu 1 (VD):

Phương pháp:

1) Bước 1: Tính $\Delta {\rm{ \;}} = {{\rm{b}}^2} - 4{\rm{ac}}$

Bước 2: So sánh $\Delta$ với 0

- $\Delta {\rm{ \;}} < 0 = {\rm{ \;}} >$ phương trình (1) vô nghiệm

- $\Delta {\rm{ \;}} = 0$ => phương trình (1) có nghiệm kép ${x_1} = {x_2} = {\rm{ \;}} - \frac{b}{{2a}}$

- $\Delta {\rm{ \;}} > 0$ => phương trình (1) có 2 nghiệm phân biệt, ta dùng công thức nghiệm sau:

2) Đặt ẩn đưa về phương trình bậc hai rồi giải.

3) Sử dụng phương pháp thế hoặc trừ vế.

Cách giải:

1) Giải phương trình ${x^2} + 8x + 15 = 0$ .

Ta có $\Delta ' = {4^2} - 1.15 = 1 > 0$ phương trình có hai nghiệm phân biệt $\left[ {\begin{array}{*{20}{c}}{{x_1} = \frac{{ - 4 + \sqrt 1 }}{1} =  - 3}\\{{x_2} = \frac{{ - 4 - \sqrt 1 }}{1} =  - 5}\end{array}} \right.$

Vậy tập nghiệm của phương trình là $S = \left\{ { - 5; - 3} \right\}$.

2) Giải phương trình ${x^4} - 3{x^2} - 4 = 0$ .

Đặt ${x^2} = t\,\,\left( {t \ge 0} \right)$ phương trình trở thành ${t^2} - 3t - 4 = 0$.

Ta có $\Delta  = {\left( { - 3} \right)^2} - 4.1.\left( { - 4} \right) = 9 + 16 = 25 > 0$ nên phương trình có hai nghiệm phân biệt:

$\left[ {\begin{array}{*{20}{c}}{{t_1} = \frac{{3 - \sqrt {25} }}{{2.1}} =  - 1\,\,\,\,\,(ktm)}\\{{t_2} = \frac{{3 + \sqrt {25} }}{{2.1}} = 4\,\,\,\left( {tm} \right)}\end{array}} \right.$

Trở lại phép đặt ta có: $t = 4 \Leftrightarrow {x^2} = 4 \Leftrightarrow x =  \pm 2$

Vậy tập nghiệm của phương trình là$S = \left\{ {2; - 2} \right\}$.

3) Giải hệ phương trình $\left\{ {\begin{array}{*{20}{l}}{2x + 3y = 13}\\{x - 3y = 2}\end{array}} \right.$ .

Cộng vế với vế ta được:

$\left\{ {\begin{array}{*{20}{c}}{3x = 15}\\{x - 3y = 2}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{x = 5}\\{x - 3y = 2}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{x = 5}\\{ - 3y =  - 3}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{x = 5}\\{y = 1}\end{array}} \right.$

Vậy hệ phương trình có nghiệm $\left( {x;y} \right) = \left( {5;1} \right)$.

Câu 2 (VD):

Phương pháp:

Với ${\rm{A}}$ là một biểu thức ta có $\sqrt {{A^2}} {\rm{ \;}} = |A|$ nghĩa là:

- $\sqrt {{A^2}} {\rm{ \;}} = A$ nếu ${\rm{A}} \ge 0$.

- $\sqrt {{A^2}} {\rm{ \;}} = {\rm{ \;}} - A$ nếu ${\rm{A}} < 0$.

Cách giải:

Rút gọn biểu thức $A = \sqrt {{{\left( {\sqrt 2  - 1} \right)}^2}}  - \frac{1}{3}\sqrt {18}$ .

Ta có:

$\begin{array}{l}A = \sqrt {{{\left( {\sqrt 2  - 1} \right)}^2}}  - \frac{1}{3}\sqrt {18} \\A = \left| {\sqrt 2  - 1} \right| - \frac{1}{3}\sqrt {{3^2}.2} \\A = \sqrt 2  - 1 - \frac{1}{3}.3.\sqrt 2 \,\,\left( {do\,\,\sqrt 2  - 1 > 0} \right)\\A = \sqrt 2  - 1 - \sqrt 2 \\A =  - 1\end{array}$

Vậy A = -1.

Câu 3 (NB):

Phương pháp:

1) Vẽ đồ thị.

2) Tìm toạ độ giao điểm.

3) Sử dụng định lí vi - et

Cách giải:

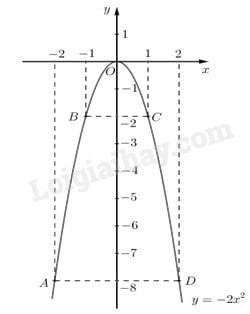
1) Vẽ đồ thị hàm số $y =  - 2{x^2}$.

Ta có bảng giá trị sau:

$\Rightarrow$ Đồ thị hàm số là đường cong parabol đi qua các điểm $O\,\left( {0;0} \right);A\left( { - 2; - 8} \right);\,\,B\left( { - 1; - 2} \right);C\left( { - 1; - 2} \right);\,\,D\left( {2; - 8} \right)$

Hệ số $a =  - 2 < 0$ nên parabol có bề cong hướng xuống. Đồ thị hàm số nhận Oy làm trục đối xứng.

Ta vẽ được đồ thị hàm số $y =  - 2{x^2}$ như sau:

2) Tìm tham số thực $m$ để đồ thị hàm số $y =  - 2{x^2}$ và đường thẳng $y = x - m$ có điểm chung.

Xét phương trình hoành độ giao điểm của đồ thị hàm số $y =  - 2{x^2}$ và đường thẳng $y = x - m$, ta có:

$- 2{x^2} = x - m \Leftrightarrow  - 2{x^2} - x + m = 0$

Để đồ thị hàm số $y =  - 2{x^2}$ và đường thẳng $y = x - m$ có điểm chung thì phương trình $- 2{x^2} - x + m = 0$ phải có nghiệm.

$\Leftrightarrow \Delta  = {( - 1)^2} - 4.( - 2).m = 1 + 8m \ge 0 \Leftrightarrow m \ge \frac{{ - 1}}{8}$

Vậy $m \ge \frac{{ - 1}}{8}$ thì đồ thị hàm số $y =  - 2{x^2}$ và đường thẳng $y = x - m$ có điểm chung.

3) Cho phương trình $3{x^2} + 5x - 1 = 0$ có hai nghiệm ${x_1},{x_2}.$Tính giá trị biểu thức $T = 6{x_1} - 7{x_1}{x_2} + 6{x_2}$.

Vì phương trình có hai nghiệm phân biệt nên theo hệ thức Viet ta có: $\left\{ \begin{array}{l}{x_1} + {x_2} =  - \frac{5}{3}\\{x_1}.{x_2} =  - \frac{1}{3}\end{array} \right.$

Khi đó ta có:

$T = 6{x_1} - 7{x_1}{x_2} + 6{x_2}$

$\begin{array}{l} = 6\left( {{x_1} + {x_2}} \right) - 7{x_1}{x_2}\\ = 6.\left( { - \frac{5}{3}} \right) - 7.\left( { - \frac{1}{3}} \right)\\ =  - \frac{{23}}{3}\end{array}$

Vậy $T =  - \frac{{23}}{3}$.

Câu 4 (VD):

Cách giải:

1) Gọi hai vòi chảy riêng đầy bể lần lượt là $x,y$ (phút, $x,y > 40$)

Mỗi giờ vòi thứ nhất chảy một mình được $\frac{1}{x}$ (bể), vòi thứ hai chảy một mình được $\frac{1}{y}$ (bể)

Vì 2 vòi cùng chảy vào bể sau 40 phút thì đầy bể nên ta có:

$\frac{1}{x} + \frac{1}{y} = \frac{1}{{40}}$ (1)

Vì nếu mở vòi thứ nhất chảy trong 15 phút rồi khóa lại, sau đó mở vòi thứ hai chảy tiếp trong 20 phút thì lúc này lượng nước trong bể chiếm $\frac{5}{{12}}$ thể tích của bể nước nên ta có:

$\frac{{15}}{x} + \frac{{20}}{y} = \frac{5}{{12}}$ (2)

Từ (1) và (2) ta có hệ phương trình: $\left\{ \begin{array}{l}\frac{1}{x} + \frac{1}{y} = \frac{1}{{40}}\\\frac{{15}}{x} + \frac{{20}}{y} = \frac{5}{{12}}\end{array} \right.$.

Đặt $\left\{ \begin{array}{l}u = \frac{1}{x}\\v = \frac{1}{y}\end{array} \right.$, hệ phương trình trở thành $\left\{ \begin{array}{l}u + v = \frac{1}{{40}}\\15u + 20v = \frac{5}{{12}}\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}15u + 15v = \frac{3}{8}\\15u + 20v = \frac{5}{{12}}\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}5v = \frac{1}{{24}}\\u = \frac{1}{{40}} - v\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}v = \frac{1}{{120}}\\u = \frac{1}{{60}}\end{array} \right.$.

$\Rightarrow \left\{ \begin{array}{l}\frac{1}{x} = \frac{1}{{60}}\\\frac{1}{y} = \frac{1}{{120}}\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 60\\y = 120\end{array} \right.\,\,\left( {TM} \right)$.

Vậy vòi 1 chảy một mình đầy bể trong 60 phút, vòi 2 chảy một mình đầy bể trong 120 phút.

2) Gọi $h$ là đường cao của hình nón.

Ta có: ${r^2} + {h^2} = {l^2} \Leftrightarrow {6^2} + {h^2} = {10^2} \Leftrightarrow {h^2} = 64 \Leftrightarrow h = 8$ (cm).

Thể tích của hình nón là: $V = \frac{1}{3}\pi {r^2}h = \frac{1}{3}\pi {.6^2}.8 = 96\pi \,\left( {c{m^3}} \right)$.

Vậy thể tích của hình nón là: $96\pi \left( {c{m^3}} \right).$

Câu 5 (VD):

Cách giải:

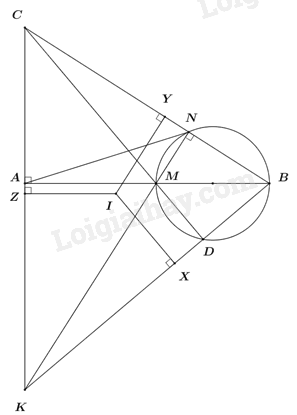
1) Chứng minh tứ giác AMNC  nội tiếp.

Xét tứ giác AMNC có:

$\angle CAM = {90^0}$ ($\Delta ABC$ vuông tại A)

$\angle CNM = {90^0}$ (do $MN \bot AC$)

$\Rightarrow \angle CAM + \angle CAN = {90^0} + {90^0} = {180^0}$

Suy ra tứ giác AMNC nội tiếp. (tứ giác có tổng hai góc đối bằng ${180^0}$).

2) Chứng minh $\angle ABK = \angle ACM$ .

Vì AMNC là tứ giác nội tiếp (cmt) $\Rightarrow \angle ACM = \angle ANM$ (hai góc nội tiếp cùng chắn cung AM)  (1)

Xét tứ giác ANBK có: $\angle KAB = \angle KNB = {90^0}\,\,\left( {gt} \right)$

Mà hai góc này ở vị trí hai góc kề nhau cùng chắn BK.

=> ANBK là tứ giác nội tiếp (dhnb)

$\Rightarrow \angle ABK = \angle ANK = \angle ANM$ (hai góc nội tiếp cùng chắn cung AK)  (2)

Từ (1) và (2) $\Rightarrow \angle ABK = \angle ACM\,\,\left( {dpcm} \right)$.

3) Đoạn thẳng  BK  cắt đường tròn đường kính  BM  tại điểm D (D khác  B). Gọi I là tâm và $r$ là bán kính của đường tròn nội tiếp tam giác BKC . Chứng minh $\frac{1}{r} = \frac{1}{{KN}} + \frac{1}{{CD}} + \frac{1}{{AB}}$ .

Ta có: $\left\{ \begin{array}{l}KN \bot BC\\AB \bot CK\\KN \cap AB = \left\{ M \right\}\end{array} \right. \Rightarrow M$ là trực tâm tam giác BCK.

$\Rightarrow CM$ là đường cao thứ ba của tam giác BCK $\Rightarrow CM \bot BK$.

Mà $\angle MDB = {90^0}$ (góc nội tiếp chắn nửa đường tròn) $\Rightarrow MD \bot BD \Rightarrow MD \bot BK$

=> C, M, D thẳng hàng.

Gọi X, Y, Z lần lượt là hình chiếu vuông góc của I trên BK, BC, CK.

Ta có:

$\begin{array}{l}{S_{\Delta BCK}} = {S_{\Delta IBK}} + {S_{\Delta IBC}} + {S_{\Delta ICK}}\\\,\,\,\,\,\,\,\,\,\,\,\,\, = \frac{1}{2}\left( {IX.BK + IY.BC + IZ.CK} \right)\\\,\,\,\,\,\,\,\,\,\,\,\,\, = r.\frac{{BK + BC + CK}}{2}\end{array}$

Mặt khác:

$\begin{array}{l}{S_{\Delta BCK}} = \frac{1}{2}CD.BK = \frac{1}{2}KN.BC = \frac{1}{2}AB.CK\\ \Rightarrow BK = \frac{{2{S_{\Delta BCK}}}}{{CD}},\,\,BC = \frac{{2{S_{\Delta BCK}}}}{{KN}},\,\,CK = \frac{{2{S_{\Delta BCK}}}}{{AB}}\end{array}$

Do đó ta có:

$\begin{array}{l}{S_{\Delta BCK}} = r.\frac{{\frac{{2{S_{\Delta BCK}}}}{{CD}} + \frac{{2{S_{\Delta BCK}}}}{{KN}} + \frac{{2{S_{\Delta BCK}}}}{{AB}}}}{2}\\ \Rightarrow {S_{\Delta BCK}} = r.\frac{{2{S_{\Delta BCK}}\left( {\frac{1}{{CD}} + \frac{1}{{KN}} + \frac{1}{{AB}}} \right)}}{2}\\ \Rightarrow 1 = r.\left( {\frac{1}{{CD}} + \frac{1}{{KN}} + \frac{1}{{AB}}} \right)\\ \Leftrightarrow \frac{1}{r} = \frac{1}{{CD}} + \frac{1}{{KN}} + \frac{1}{{AB}}\,\,\left( {dpcm} \right).\end{array}$