Đề thi vào 10 môn Toán Hà Nội năm 2017
Tải vềBài I (2,0 điểm) Cho hai biểu thức
Đề bài
Bài I (2,0 điểm)
Cho hai biểu thức \(A = \dfrac{{\sqrt x + 2}}{{\sqrt x - 5}}\) và \(B = \dfrac{3}{{\sqrt x + 5}} + \dfrac{{20 - 2\sqrt x }}{{x - 25}}\), với \(x \ge 0,x \ne 25.\)
1) Tính giá trị của biểu thức A khi x = 9.
2) Chứng minh \(B = \dfrac{1}{{\sqrt x - 5}}\).
3) Tìm tất cả các giá trị của x để \(A = B.\left| {x - 4} \right|\).
Bài II (2,0 điểm )
Giải bài toán sau bằng cách lập phương trình hoặc hệ phương trình
Một xe ô tô và xe máy cùng khởi hành từ A để đi đến B với vận tốc của mỗi xe không đổi trên toàn bộ quãng đường AB dài 120 km. Do vận tốc xe ô tô lớn hơn vận tốc xe máy là 10 km/h nên xe ô tô đến B sớm hơn xe máy 36 phút. Tính vận tốc của mỗi xe.
Bài III(2 điểm)
1) Giải hệ phương trình: \(\left\{ \begin{array}{l}\sqrt x + 2\sqrt {y - 1} = 5\\4\sqrt x - \sqrt {y - 1} = 2\end{array} \right.\).
2) Trong mặt phẳng toạ độ \(Oxy\), cho đường thẳng (d): \(y = mx + 5\).
a) Chứng minh đường thẳng (d) luôn đi qua điểm A(0; 5) với mọi giá trị của m.
b) Tìm tất cả các giá trị của m để đường thẳng (d) cắt parabol (P): \(y = {x^2}\) tại hai điểm phân biệt có hoành độ lần lượt là \({x_1};\,\,{x_2}\)(với \({x_1} < {x_2}\)) sao cho \(\left| {{x_1}} \right| > \left| {{x_2}} \right|\).
Bài IV(3,5 điểm)
Cho đường tròn (O) ngoại tiếp tam giác nhọn ABC. Gọi M và N lần lượt là điểm chính giữa cung nhỏ AB và cung nhỏ BC. Hai dây AN và CM cắt nhau tại điểm I. Dây MN Cắt các cạnh AB và BC lần lươt tại các điểm H và K.
1) Chứng minh bốn điểm C, N, K, I cùng thuộc một đường tròn.
2) Chứng minh \(N{B^2} = NK.NM\)
3) Chứng minh tứ giác BHIK là hình thoi
4) Gọi P, Q lần lượt là tâm của các đường tròn ngọai tiếp tam giác MBK, tam giác MCK và E là trung điểm của đoạn PQ. Vẽ đường kính ND của đường tròn (O). Chứng minh ba điểm D, E, K thẳng hàng.
Bài V (0,5 điểm)
Cho các số thực a, b, c thay đổi luôn thỏa mãn: \(a \ge 1,b \ge 1,c \ge 1\) \(ab + bc + ca = 9\) . Tìm giá trị nhỏ nhất và giá trị lớn nhất của biểu thức \(P = {a^2} + {b^2} + {c^2}\) .
Lời giải chi tiết
|
Bài I Cho hai biểu thức \(A = \dfrac{{\sqrt x + 2}}{{\sqrt x - 5}}\) và \(B = \dfrac{3}{{\sqrt x + 5}} + \dfrac{{20 - 2\sqrt x }}{{x - 25}}\), với \(x \ge 0,x \ne 25.\) 1) Tính giá trị của biểu thức A khi x = 9. 2) Chứng minh \(B = \dfrac{1}{{\sqrt x - 5}}\). 3) Tìm tất cả các giá trị của x để \(A = B.\left| {x - 4} \right|\). |
Hướng dẫn giải:
1) Khi x = 9 ta có: \(A = \dfrac{{\sqrt 9 + 2}}{{\sqrt 9 - 5}} = \dfrac{{\sqrt {{3^2}} + 2}}{{\sqrt {{3^2}} - 5}} = \dfrac{{3 + 2}}{{3 - 5}} = - \dfrac{5}{2}\)
2) Với \(x \ge 0,x \ne 25.\)
\(\begin{array}{l}B = \dfrac{3}{{\sqrt x + 5}} + \dfrac{{20 - 2\sqrt x }}{{x - 25}}\\ = \dfrac{{3\left( {\sqrt x - 5} \right)}}{{\left( {\sqrt x - 5} \right)\left( {\sqrt x + 5} \right)}} + \dfrac{{20 - 2\sqrt x }}{{\left( {\sqrt x - 5} \right)\left( {\sqrt x + 5} \right)}}\\ = \dfrac{{3\left( {\sqrt x - 5} \right) + 20 - 2\sqrt x }}{{\left( {\sqrt x - 5} \right)\left( {\sqrt x + 5} \right)}}\\ = \dfrac{{3\sqrt x - 15 + 20 - 2\sqrt x }}{{\left( {\sqrt x - 5} \right)\left( {\sqrt x + 5} \right)}}\\ = \dfrac{{\sqrt x + 5}}{{\left( {\sqrt x - 5} \right)\left( {\sqrt x + 5} \right)}}\\ = \dfrac{1}{{\sqrt x - 5}}\end{array}\)
Ta có điều phải chứng minh.
3) với \(x \ge 0,x \ne 25.\)
\(A = B.\left| {x - 4} \right|\)
\(\begin{array}{l} \Leftrightarrow \dfrac{{\sqrt x + 2}}{{\sqrt x - 5}} = \dfrac{1}{{\sqrt x - 5}}\left| {x - 4} \right|\\ \Leftrightarrow \sqrt x + 2 = \left| {x - 4} \right|(1)\end{array}\)
TH1: Nếu \(x \ge 4,x \ne 25\) ta được (1) trở thành: \(\sqrt x + 2 = x - 4 \Leftrightarrow x - \sqrt x - 6 = 0 \Leftrightarrow \left( {\sqrt x + 2} \right)\left( {\sqrt x - 3} \right) = 0 \Leftrightarrow \left[ \begin{array}{l}\sqrt x = 3 \Leftrightarrow x = 9(tm)\\\sqrt x = - 2(ktm)\end{array} \right.\)
TH2: Nếu \(0 \le x < 4\) ta được (1) trở thành:
\(\sqrt x + 2 = - x + 4 \Leftrightarrow x + \sqrt x - 2 = 0 \Leftrightarrow \left( {\sqrt x - 1} \right)\left( {\sqrt x + 2} \right) = 0 \Leftrightarrow \left[ \begin{array}{l}\sqrt x = 1 \Leftrightarrow x = 1(tm)\\\sqrt x = - 2(ktm)\end{array} \right.\)
Vậy x = 9, x = 1 thỏa mãn yêu cầu bài toán.
|
Bài II Giải bài toán sau bằng cách lập phương trình hoặc hệ phương trình Một xe ô tô và xe máy cùng khởi hành từ A để đi đến B với vận tốc của mỗi xe không đổi trên toàn bộ quãng đường AB dài 120 km. Do vận tốc xe ô tô lớn hơn vận tốc xe máy là 10 km/h nên xe ô tô đến B sớm hơn xe máy 36 phút. Tính vận tốc của mỗi xe. |
Hướng dẫn giải.
Cách 1:
Gọi vận tốc của ô tô là x (km/h) (ĐK: x>10 )
Do vận tốc của ô tô lớn hớn vận tốc cả xe máy là 10 km/h nên vận tốc của xe máy là x-10 (km/h)
Thời gian ô tô đi từ A đến B là \(\dfrac{{120}}{x}\) (h)
Thời gian xe máy đi từ A đến B là \(\dfrac{{120}}{{x - 10}}\) (h)
Vì ô tô đến B sớm hơn xe máy 36 phút =\(\dfrac{3}{5}\) giờ nên ta có phương trình:
\(\begin{array}{l}\dfrac{{120}}{{x - 10}} - \dfrac{{120}}{x} = \dfrac{3}{5}\,\, \Leftrightarrow 120\left( {\dfrac{1}{{x - 10}} - \dfrac{1}{x}} \right) = \dfrac{3}{5} \Leftrightarrow \dfrac{1}{{x - 10}} - \dfrac{1}{x} = \dfrac{1}{{200}}\\ \Leftrightarrow \dfrac{{x - x + 10}}{{\left( {x - 10} \right)x}} = \dfrac{1}{{200}}\\ \Rightarrow x\left( {x - 10} \right) = 2000 \Leftrightarrow {x^2} - 10x - 2000 = 0\\ \Leftrightarrow \left( {x - 50} \right)\left( {x + 40} \right) = 0\\ \Leftrightarrow \left[ \begin{array}{l}x = 50(tmdk)\\x = - 40(ktmdk)\end{array} \right.\end{array}\)
Vậy vận tốc của ô tô là 50 km/h và vận tốc của xe máy là 40 km/h.
Cách 2:
Gọi vận tốc của ô tô là x, vận tốc của xe máy là y (km/h) (ĐK: x>10; y>0 )
Do vận tốc của ô tô lớn hơn vận tốc cả xe máy là 10 km/h nên ta có phương trình \(x - y = 10\,\,\,\,(1)\)
Thời gian ô tô đi từ A đến B là \(\dfrac{{120}}{x}\) (h)
Thời gian xe máy đi từ A đến B là \(\dfrac{{120}}{y}\) (h)
Vì ô tô đến B sớm hơn xe máy 36 phút =\(\dfrac{3}{5}\) giờ nên ta có phương trình:
\(\dfrac{{120}}{y} - \dfrac{{120}}{x} = \dfrac{3}{5}\,\,\,(2)\)
Từ (1) và (2) ta có hệ phương trình:
\(\begin{array}{l}\left\{ \begin{array}{l}x - y = 10\\\dfrac{{120}}{y} - \dfrac{{120}}{x} = \dfrac{3}{5}\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x - y = 10\\120\left( {\dfrac{1}{y} - \dfrac{1}{x}} \right) = \dfrac{3}{5}\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x - y = 10\\\dfrac{1}{y} - \dfrac{1}{x} = \dfrac{1}{{200}}\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}x - y = 10\\\dfrac{{x - y}}{{xy}} = \dfrac{1}{{200}}\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x - y = 10\\xy = 2000\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 10 + y\\\left( {10 + y} \right)y = 2000\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}x = 10 + y\\{y^2} + 10y - 2000 = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 10 + y\\\left[ \begin{array}{l}y = 40\,\,\,\,\,\,(tm)\\y = - 50\,\,\,(ktm)\end{array} \right.\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 50\\y = 40\end{array} \right.(tm)\end{array}\)
Vậy vận tốc của ô tô là 50 km/h và vận tốc của xe máy là 40 km/h.
|
Bài III: 1) Giải hệ phương trình: \(\left\{ \begin{array}{l}\sqrt x + 2\sqrt {y - 1} = 5\\4\sqrt x - \sqrt {y - 1} = 2\end{array} \right.\). 2) Trong mặt phẳng toạ độ \(Oxy\), cho đường thẳng (d): \(y = mx + 5\). a) Chứng minh đường thẳng (d) luôn đi qua điểm A(0; 5) với mọi giá trị của m. b) Tìm tất cả các giá trị của m để đường thẳng (d) cắt parabol (P): \(y = {x^2}\) tại hai điểm phân biệt có hoành độ lần lượt là \({x_1};\,\,{x_2}\)(với \({x_1} < {x_2}\)) sao cho \(\left| {{x_1}} \right| > \left| {{x_2}} \right|\). |
Hướng dẫn giải:
1) ĐKXĐ: \(\left\{ \begin{array}{l}x \ge 0\\y \ge 1\end{array} \right.\).
Đặt \(\left\{ \begin{array}{l}\sqrt x = a \ge 0\\\sqrt {y - 1} = b \ge 0\end{array} \right.\). Khi đó ta có hệ phương trình:
\(\left\{ \begin{array}{l}a + 2b = 5\\4a - b = 2\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a = 5 - 2b\\4\left( {5 - 2b} \right) - b = 2\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a = 5 - 2b\\9b = 18\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a = 5 - 2b\\b = 2\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a = 1\left( {tm} \right)\\b = 2\left( {tm} \right)\end{array} \right.\)
\( \Leftrightarrow \left\{ \begin{array}{l}\sqrt x = 1\\\sqrt {y - 1} = 2\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 1\\y - 1 = 4\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 1\left( {tm} \right)\\y = 5\left( {tm} \right)\end{array} \right.\)
Vậy hệ phương trình có nghiệm duy nhất: \(\left( {x;y} \right) = \left( {1;5} \right)\).
2) Ta có: (d): \(y = mx + 5\).
a) Thay tọa độ điểm A(0; 5) vào (d) ta được: 5 = m. 0 + 5 ( luôn đúng)
Vậy đường thẳng (d) luôn đi qua điểm A(0; 5) với mọi giá trị của m.
b) Phương trình hoành độ giao điểm của (d) và (P) là: \({x^2} = mx + 5 \Leftrightarrow {x^2} - mx - 5 = 0\) (*)
Đường thẳng (d) cắt (P) tại hai điểm phân biệt \( \Leftrightarrow \) phương trình (*) có hai nghiệm phân biệt
\( \Leftrightarrow \Delta > 0 \Leftrightarrow {m^2} + 20 > 0\,\,\,\forall m\)
Vậy đường thẳng (d) luôn cắt (P) tại hai điểm phân biệt \({x_1};\,\,{x_2}\) với mọi m.
Theo hệ thức Vi-ét ta có: \(\left\{ \begin{array}{l}{x_1} + {x_2} = m\\{x_1}{x_2} = - 5\end{array} \right.\)
Vì a.c < 0 nên phương trình luôn có 2 nghiệm phân biệt trái dấu \({x_1} < 0 < \,{x_2}\)
Để \(\left| {{x_1}} \right| > \left| {{x_2}} \right|\) thì \({x_1} + \,{x_2} < 0 \Leftrightarrow m < 0\)
Vậy \(m < 0\) thỏa mãn điều kiện bài toán.
|
Bài IV Cho đường tròn (O) ngoại tiếp tam giác nhọn ABC. Gọi M và N lần lượt là điểm chính giữa cung nhỏ AB và cung nhỏ BC. Hai dây AN và CM cắt nhau tại điểm I. Dây MN Cắt các cạnh AB và BC lần lươt tại các điểm H và K. 1) Chứng minh bốn điểm C, N, K, I cùng thuộc một đường tròn. 2) Chứng minh \(N{B^2} = NK.NM\) 3) Chứng minh tứ giác BHIK là hình thoi 4) Gọi P, Q lần lượt là tâm của các đường tròn ngọai tiếp tam giác MBK, tam giác MCK và E là trung điểm của đoạn PQ. Vẽ đường kính ND của đường tròn (O). Chứng minh ba điểm D, E, K thẳng hàng. |
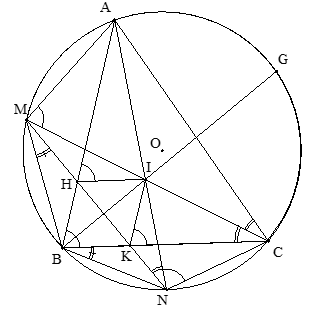
1) Vì M là điểm chính giữa cung nhỏ AB của (O) (giả thiết)
Suy ra cung AM = cung MB
⇒ góc ACM = góc BCM (hai góc nội tiếp chắn hai cung bằng nhau)
Mà góc ACM = góc ANM (hai góc nội tiếp cùng chắn cung AM)
⇒ góc MNA = góc BCM hay góc KNI = góc KCI
Xét tứ giác IKNC:
Góc KNI = góc KCI (cmt)
Mà C và N là hai đỉnh kề nhau
⇒ IKNC là tứ giác nội tiếp (dấu hiệu nhận biết tứ giác nội tiếp)
⇒ 4 điểm C, N, K, I cùng thuộc một đường tròn
2) Vì ABNC là tứ giác nội tiếp nên góc NBC = góc NAC
Vì N là điểm chính giữa cung nhỏ BC của (O) nên góc NAC = góc NAB
Vì AMBN là tứ giác nội tiếp nên góc NAB = góc NMB
Suy ra góc NBC = góc NMB hay góc NBK = góc NMB
Xét ∆ NBK và ∆ NMB có góc NBK = góc NMB; góc MNB chung nên
![]()
3)
Tứ giác IKNC nội tiếp suy ra góc IKC = góc INC (hai góc nội tiếp cùng chắn cung IC)
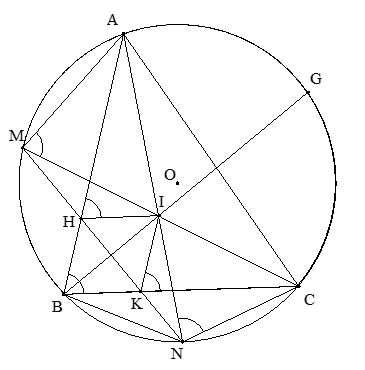
Xét (O): Góc ABC = góc ANC ( hai góc nội tiếp cùng chắn cung AC)
Suy ra góc ABC = góc IKC
Mà hai góc này ở vị trí đồng vị
Suy ra IK//HB (dhnb hai đt song song)
BI cắt (O) tại G.
Vì I là giao điểm ba đường phân giác của tam giác ABC nên G là điểm chính giữa cung AC và BI là phân giác góc ABC
Chứng minh tương tự câu a ta có tứ giác AMHI nội tiếp
Suy ra góc AHI = góc AMI (hai góc nội tiếp cùng chắn cung AI)
Xét (O): Góc ABC = góc AMC ( hai góc nội tiếp cùng chắn cung AC)
Suy ra góc ABC = góc AHI
Mà hai góc này ở vị trí đồng vị
Suy ra HI//BK (dhnb hai đt song song)
Xét tứ giác BHIK:
IK//HB ( cmt)
HI//BK (cmt)
Suy ra tứ giác BHIK là hình bình hành (dhnb HBH)
Mà BI là phân giác của góc HBK (cmt)
Suy ra tứ giác BHIK là hình thoi. (dhnb hình thoi)
4)
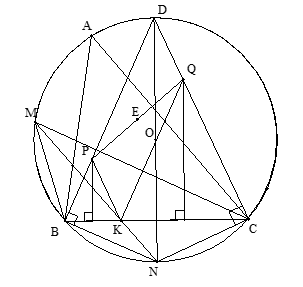
Vì góc NBK = góc BMK nên ta có BN là tiếp tuyến tại B của đường tròn (P) ngoại tiếp ∆MBK ⇒ BN ⊥ BP
Mà BN ⊥ BD do góc DBN = 90 o (góc nội tiếp chắn nửa đường tròn)
⇒ B, P, D thẳng hàng
Tương tự ta có C, Q, D thẳng hàng
∆ PBK và ∆ DBC là 2 tam giác cân có chung góc ở đáy nên góc ở đỉnh của chúng bằng nhau
⇒ góc BPK = góc BDC
⇒ PK // DC ⇒ PK // DQ
Tương tự ta có DP // QK
Vậy DPKQ là hình bình hành ⇒ DK đi qua trung điểm PQ
⇒ D, E, K thẳng hàng.
|
Bài V Cho các số thực a, b, c thay đổi luôn thỏa mãn: \(a \ge 1,b \ge 1,c \ge 1\) \(ab + bc + ca = 9\) . Tìm giá trị nhỏ nhất và giá trị lớn nhất của biểu thức \(P = {a^2} + {b^2} + {c^2}\) . |
Hướng dẫn giải
+ Áp dụng bất đẳng thức Côsi cho 2 số dương ta có
\(\left\{ \begin{array}{l}{a^2} + {b^2} \ge 2ab\\{b^2} + {c^2} \ge 2bc\\{c^2} + {a^2} \ge 2ca\end{array} \right. \Rightarrow 2\left( {{a^2} + {b^2} + {c^2}} \right) \ge 2\left( {ab + bc + ca} \right)\)
\( \Rightarrow P = {a^2} + {b^2} + {c^2} \ge ab + bc + ca = 9\)
Dấu “=” xảy ra ⇔ \(\left\{ \begin{array}{l}a = b = c \ge 1\\ab + bc + ca = 9\end{array} \right. \Leftrightarrow a = b = c = \sqrt 3 \)
+ Vì \(\left\{ \begin{array}{l}a \ge 1\\b \ge 1\\c \ge 1\end{array} \right. \Rightarrow \left\{ \begin{array}{l}\left( {a - 1} \right)\left( {b - 1} \right) \ge 0\\\left( {b - 1} \right)\left( {c - 1} \right) \ge 0\\\left( {c - 1} \right)\left( {a - 1} \right) \ge 0\end{array} \right. \Rightarrow \left\{ \begin{array}{l}ab - a - b + 1 \ge 0\\bc - b - c + 1 \ge 0\\ca - c - a + 1 \ge 0\end{array} \right.\)
\(\begin{array}{l} \Rightarrow ab + bc + ca - 2\left( {a + b + c} \right) + 3 \ge 0\\ \Rightarrow a + b + c \le \dfrac{{ab + bc + ca + 3}}{2}\end{array}\)
Vì \(a \le 1;b \le 1;c \le 1\)
\( \Rightarrow 3 \le a + b + c \le \dfrac{{ab + bc + ca + 3}}{2} = 6\)
\(\begin{array}{l} \Rightarrow {\left( {a + b + c} \right)^2} \le 36 \Rightarrow {a^2} + {b^2} + {c^2} + 2\left( {ab + bc + ca} \right) \le 36\\ \Rightarrow P \le 36 - 2\left( {ab + bc + ca} \right) = 18\end{array}\)
Dấu “=” xảy ra ⇔ \(\left[ \begin{array}{l}a = b = 1,c = 4\\a = 4,b = c = 1\\a = c = 1,b = 4\end{array} \right.\)
Vậy GTNN của P là 9, xảy ra khi và chỉ khi \(a = b = c = \sqrt 3 \); GTLN của P là 18, xảy ra khi và chỉ khi \(\left[ \begin{array}{l}a = b = 1,c = 4\\a = 4,b = c = 1\\a = c = 1,b = 4\end{array} \right.\).