Đề thi vào 10 môn Toán Phú Thọ năm 2020
Tải vềPHẦN 1: TRẮC NGHIỆM KHÁCH QUAN (2,5 điểm) Câu 1. Điều kiện xác định của biểu thức
Đề bài
PHẦN 1: TRẮC NGHIỆM KHÁCH QUAN (2,5 điểm)
Câu 1. Điều kiện xác định của biểu thức \(\sqrt {2020 - x} \) là
A.\(x \le 2020\) B. \(x \ge 2020\) C. \(x < 2020\) D. \(x > 2020\)
Câu 2. Có bao nhiêu hàm số đồng biến trên ℝ trong các hàm số sau \(y = 17x + 2;y = 17x - 8;y = 11 - 5x;y = x + 10;y = - x + 2020?\)
A. 5 B. 4 C. 3 D. 2
Câu 3. Cho hàm số \(y = \left( {m - 3} \right)x\) có đồ thị như hình vẽ dưới đây.
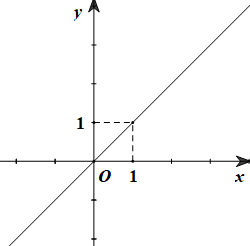
Khẳng định nào sau đây đúng ?
A. m = –4
B. m = –3
C. m = 3
D. m = 4
Câu 4. Hệ phương trình \(\left\{ \begin{array}{l} - 5x + 3y = 1\\x + 5y = 11\end{array} \right.\) có nghiệm là\(\left( {x;y} \right)\). Khi đó \(x - y\) bằng
A. –1 B. 1 C. 3 D. 4
Câu 5. Điểm nào sau đây không thuộc đồ thị hàm số\(y = 5{x^2}\)?
A. A (1;5) B. B (3;40) C. C (2;20) D. D (–1;5)
Câu 6. Giả sử phương trình \({x^2} - 16x + 55 = 0\) có hai nghiệm \({x_1},{x_2}\left( {{x_1} < {x_2}} \right)\). Tính \({x_1} - 2{x_2}\)
A. 1 B. 24 C. 13 D. –17
Câu 7. Cho parabol \(y = {x^2}\) và đường thẳng \(y = - 2x + 3\) cắt nhau tại hai điểm\(A\left( {{x_1};{y_1}} \right);B\left( {{x_2};{y_2}} \right)\). Khi đó \({y_1} + {y_2}\) bằng:
A. 1 B. –2 C. 8 D. 10
Câu 8. Cho tam giác ABC vuông cân tại A , cạnh \(BC = \sqrt 6 \left( {cm} \right)\). Diện tích tam giác ABC bằng:
A. \(\sqrt 3 \left( {c{m^2}} \right)\) B. \(3\left( {c{m^2}} \right)\) C. \(\dfrac{3}{2}\left( {c{m^2}} \right)\) D. \(6\left( {c{m^2}} \right)\)
Câu 9. Cho hai đường tròn \(\left( O \right)\) và \(\left( {O'} \right)\) cắt nhau tại A và B. Biết\(OA = 6\left( {cm} \right);AO' = 5\left( {cm} \right);AB = 8\left( {cm} \right)\). (như hình vẽ bên).
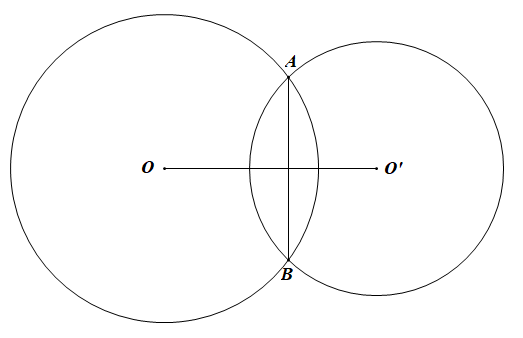
Độ dài GO’ bằng
A. 5 ( cm )
B. \(5\sqrt 5 \left( {cm} \right)\)
C. \(3 + 2\sqrt 5 \left( {cm} \right)\)
D. \(3 + 5\sqrt 2 \left( {cm} \right)\)
Câu 10. Cho hình vuông ABCD nội tiếp đường tròn tâm O . Gọi M, N lần lượt là trung điểm BC, C D. Đường thẳng AM, BN cắt đường tròn lần lượt tại E, F (như hình vẽ bên).
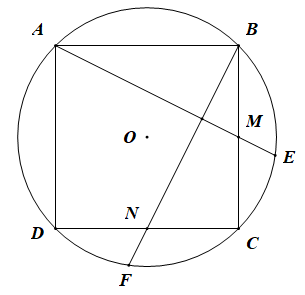
Số đo góc EDF bằng
A. \({30^0}\) B. \({45^0}\)
C. \({60^0}\) D. \({75^0}\)
PHẦN II. TỰ LUẬN (7,5 điểm)
Câu 1 (1,5 điểm):
a) Tính giá trị của biểu thức: \(P = \sqrt {45} + \sqrt {9 - 4\sqrt 5 } \)
b) Giải hệ phương trình: \(\left\{ \begin{array}{l}2x + 5y = 9\\ - 2x + 7y = 3\end{array} \right.\)
Câu 2 (2,0 điểm): Cho phương trình \({x^2} - 2mx + m - 1 = 0\)( m là tham số)
a) Giải phương trình khi m = 2
b) Chứng minh phương trình luôn có hai nghiệm phân biệt với mọi giá trị của m
c) Gọi \({x_1},{x_2}\) là hai nghiệm của phương trình . Tìm m để \(x_1^2{x_2} + m{x_1} - {x_2} = 4\)
Câu 3 (3,0 điểm): Cho ∆ ABC có 3 góc nhọn nội tiếp đường tròn ( O ). Tia phân giác góc \(\angle BAC\) cắt cạnh BC tại D và cắt đường tròn ( O ) tại M . Gọi K là hình chiếu của M trên AB. I là hình chiếu của M trên AC. Chứng minh rằng
a) AKMT là tứ giác nội tiếp
b) \(M{B^2} = M{C^2} = MD.MA\)
c) Khi đường tròn ( O ) và B;C cố định, điểm A thay đổi trên cung lớn BC thì tổng \(\dfrac{{AB}}{{MK}} + \dfrac{{AC}}{{MT}}\) có giá trị không đổi.
Câu 4. (1,0 điểm): Giải phương trình \(\sqrt {{x^2} + 3x} + \sqrt {9x + 18} = 3x + \sqrt {x + \dfrac{6}{x} + 5} \).
Lời giải chi tiết
PHẦN I. TRẮC NGHIỆM (2,5 điểm)
|
1. A |
2. C |
3. D |
4. A |
5. B |
|
6. D |
7. D |
8. C |
9. C |
10. B |
Câu 1 Phương pháp:
Biểu thức \(\sqrt A \) xác định \( \Leftrightarrow A \ge 0\)
Cách giải:
Biểu thức đã cho xác định \( \Leftrightarrow 2020 - x \ge 0 \Leftrightarrow x \le 2020\)
Chọn A.
Câu 2
Phương pháp:
Hàm số bậc nhất \(y = ax + b\) đồng biến trên ℝ khi a > 0, nghịch biến khi a < 0
Cách giải:
Có 3 hàm số đồng biến trên ℝ là \(y = 17x + 2;y = 17x - 8;y = x + 10\)
Chọn C.
Câu 3
Phương pháp:
Xác định hệ số a , từ đó tìm ra m
Cách giải:
Hàm số đã cho \(y = ax + b\) đi qua gốc O nên b = 0, đi qua điểm (1;1) nên \(1 = a.1 \Rightarrow a = 1\)
⟹ m – 3 = 1 ⟹ m = 4
Chọn D.
Câu 4
Phương pháp:
Giải hệ phương trình bằng phương pháp thế, rồi tính \(x - y\)
Cách giải:
\(\begin{array}{l}\left\{ \begin{array}{l} - 5x + 3y = 1\\x + 5y = 11\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 11 - 5y\\ - 5\left( {11 - 5y} \right) + 3y = 1\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 11 - 5y\\28y - 55 = 1\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}y = 2\\x = 1\end{array} \right.\\ \Rightarrow x - y = - 1\end{array}\)
Chọn A.
Câu 5
Phương pháp:
Thay tọa độ các điểm vào hàm số
Cách giải:
Thay tọa độ điểm B (3;40) vào công thức hàm số, ta có 40 = 5.3 2 ⟺ 40 = 45 (không thỏa mãn)
Vậy điểm B không thuộc đồ thị
Chọn B.
Câu 6
Phương pháp:
Giải phương trình, tìm \({x_1},{x_2}\)
Cách giải:
Ta có \({x^2} - 16x + 55 = 0 \Leftrightarrow \left( {x - 11} \right)\left( {x - 5} \right) = 0 \Leftrightarrow \left[ \begin{array}{l}{x_1} = 5\\{x_2} = 11\end{array} \right.\;\left( {do\;{x_1} < {x_2}} \right)\)
\( \Rightarrow {x_1} - 2{x_2} = 5 - 2.11 = - 17\)
Chọn D.
Câu 7
Phương pháp:
Viết phương trình hoành độ giao điểm, giải ra 2 nghiệm
Tìm giao điểm 2 đồ thị
Cách giải:
Xét phương trình hoành độ giao điểm của hai đồ thị hàm số
\({x^2} = - 2x + 3 \Leftrightarrow {x^2} + 2x - 3 = 0 \Leftrightarrow \left[ \begin{array}{l}x = 1\\x = - 3\end{array} \right.\)
Với \(x = 1 \Rightarrow y = 1\)
Với \(x = - 3 \Rightarrow y = 9\)
Vậy \({y_1} + {y_2} = 1 + 9 = 10\)
Chọn D.
Câu 8
Phương pháp:
Tính cạnh góc vuông của tam giác, từ đó tính diện tích
Cách giải:
Vì ABC là tam giác vuông cân nên \(AB = AC = \dfrac{{BC}}{{\sqrt 2 }} = \dfrac{{\sqrt 6 }}{{\sqrt 2 }} = \sqrt 3 \)
\( \Rightarrow {S_{ABC}} = \dfrac{1}{2}AB.AC = \dfrac{1}{2}A{B^2} = \dfrac{3}{2}\left( {c{m^2}} \right)\)
Chọn C.
Câu 9
Phương pháp:
Gọi H là giao điểm của AB và OO ’
Tính OH và O’H
Cách giải:
Gọi H là giao điểm của AB và OO’ . Vì \(OA = OB;O'A = O'B\) nên OO’ là trung trực của AB , suy ra \(AH = HB = \dfrac{{AB}}{2} = 4\left( {cm} \right)\)
Vì \(AB \bot O'O\) nên hai tam giác AHO và AHO’ vuông tại H
Áp dụng định lý Pitago ta có
\(\begin{array}{l}OH = \sqrt {O{A^2} - A{H^2}} = \sqrt {{6^2} - {4^2}} = \sqrt {20} = 2\sqrt 5 \left( {cm} \right)\\O'H = \sqrt {O'{A^2} - A{H^2}} = \sqrt {{5^2} - {4^2}} = \sqrt 9 = 3\left( {cm} \right)\\ \Rightarrow OO' = OH + O'H = 3 + 2\sqrt 5 \end{array}\)
Chọn C.
Câu 10
Phương pháp:
Chứng mình hai tam giác ABM và BCN bằng nhau
Chứng minh \(\angle EDF = \angle BDC\)
Cách giải:
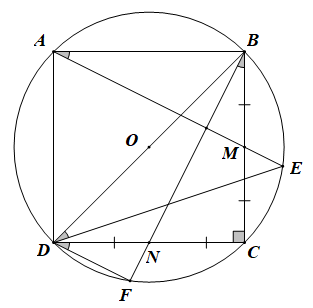
Xét hai tam giác vuông ABM và BCN có
\(\begin{array}{l}AB = BC\\\angle ABM = \angle BCN = {90^0}\\BM = CN\end{array}\)
\( \Rightarrow \Delta ABM = \Delta BCN\;\left( {c.g.c} \right)\)
\( \Rightarrow \angle BAM = \angle CBN\) (hai góc tương ứng)
Ta có các góc nội tiếp
\(\left\{ \begin{array}{l}\angle BAM = \angle BDE\\\angle CBN = \angle CDF\end{array} \right. \Rightarrow \angle BDE = \angle CDF\)
\( \Rightarrow \angle EDF = \angle CDE + \angle CDF\)\( = \angle CDE + \angle BDE = \angle BDC = {45^0}\)
(do tam giác BDC vuông cân tại C ).
Chọn B.
PHẦN II. TỰ LUẬN (7,5 điểm)
Câu 1 (1,5 điểm)
Cách giải: :
a) Tính giá trị biểu thức \(P = \sqrt {45} + \sqrt {9 - 4\sqrt 5 } \)
Ta có:
\(\begin{array}{l}P = \sqrt {45} + \sqrt {9 - 4\sqrt 5 } \\\,\,\,\,\, = \sqrt {{3^2}.5} + \sqrt {5 - 2.2\sqrt 5 + 4} \\\,\,\,\,\, = 3\sqrt 5 + \sqrt {{{\left( {\sqrt 5 - 2} \right)}^2}} \\\,\,\,\,\, = 3\sqrt 5 + \left| {\sqrt 5 - 2} \right|\\\,\,\,\,\, = 3\sqrt 5 + \sqrt 5 - 2\\\,\,\,\,\, = 4\sqrt 5 - 2\end{array}\)
Vậy \(P = 4\sqrt 5 - 2\)
b) Giải hệ phương trình \(\left\{ \begin{array}{l}2x + 5y = 9\\ - 2x + 7y = 3\end{array} \right.\)
\(\begin{array}{l}\left\{ \begin{array}{l}2x + 5y = 9\\ - 2x + 7y = 3\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}12y = 12\\2x + 5y = 9\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}y = 1\\2x + 5.1 = 9\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}y = 1\\2x = 4\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}y = 1\\x = 2\end{array} \right.\end{array}\)
Vậy hệ có nghiệm \(\left( {x;y} \right)\) là \(\left( {2;1} \right)\).
Câu 2 (2,5 điểm)
Cách giải: :
Cho phương trình \({x^2} - 2mx + m - 1 = 0\) ( \(m\) là tham số).
a) Giải phương trình khi \(m = 2\) .
Khi \(m = 2\), phương trình trở thành \({x^2} - 4x + 1 = 0\).
Ta có: \(\Delta ' = {\left( { - 2} \right)^2} - 1.1 = 3 > 0\), do đó phương trình có 2 nghiệm phân biệt \({x_1} = 2 + \sqrt 3 \), \({x_2} = 2 - \sqrt 3 \).
Vậy khi \(m = 2\) tập nghiệm của phương trình là \(S = \left\{ {2 \pm \sqrt 3 } \right\}\).
b) Chứng minh rằng phương trình luôn có hai nghiệm phân biệt với mọi giá trị của \(m\) .
Xét phương trình \({x^2} - 2mx + m - 1 = 0\) (*) ta có:
\(\begin{array}{l}\Delta ' = {m^2} - 1.\left( {m - 1} \right)\\\,\,\,\,\,\, = {m^2} - m + 1\\\,\,\,\,\,\, = {m^2} - 2.m.\dfrac{1}{2} + \dfrac{1}{4} + \dfrac{3}{4}\\\,\,\,\,\,\, = {\left( {m - \dfrac{1}{2}} \right)^2} + \dfrac{3}{4}\end{array}\)
Do \({\left( {m - \dfrac{1}{2}} \right)^2} \ge 0\,\,\forall m \Rightarrow {\left( {m - \dfrac{1}{2}} \right)^2} + \dfrac{3}{4} \ge \dfrac{3}{4} > 0\,\,\forall m\).
Vậy phương trình đã cho luôn có hai nghiệm phân biệt với mọi giá trị của \(m\).
c) Gọi \({x_1},\,\,{x_2}\) là hai nghiệm của phương trình. Tìm \(m\) để \(x_1^2{x_2} + m{x_2} - {x_2} = 4\) .
Theo ý b) phương trình luôn có hai nghiệm phân biệt với mọi \(m\).
Giả sử \({x_1},\,\,{x_2}\) là hai nghiệm của phương trình, áp dụng hệ thức Vi-ét ta có: \(\left\{ \begin{array}{l}{x_1} + {x_2} = 2m\\{x_1}{x_2} = m - 1\end{array} \right.\).
Theo bài ra ta có:
\(\begin{array}{l}\,\,\,\,\,\,x_1^2{x_2} + m{x_2} - {x_2} = 4\\ \Leftrightarrow x_1^2{x_2} + {x_2}\left( {m - 1} \right) = 4\\ \Leftrightarrow x_1^2{x_2} + {x_2}.{x_1}{x_2} = 4\\ \Leftrightarrow {x_1}{x_2}\left( {{x_1} + {x_2}} \right) = 4\\ \Leftrightarrow \left( {m - 1} \right).2m = 4\\ \Leftrightarrow m\left( {m - 1} \right) = 2\\ \Leftrightarrow {m^2} - m - 2 = 0\\ \Leftrightarrow {m^2} + m - 2m - 2 = 0\\ \Leftrightarrow m\left( {m + 1} \right) - 2\left( {m + 1} \right) = 0\\ \Leftrightarrow \left( {m + 1} \right)\left( {m - 2} \right) = 0\\ \Leftrightarrow \left[ \begin{array}{l}m + 1 = 0\\m - 2 = 0\end{array} \right.\\ \Leftrightarrow \left[ \begin{array}{l}m = - 1\\m = 2\end{array} \right.\end{array}\)
Vậy \(m = - 1,\,\,m = 2\) thỏa mãn yêu cầu bài toán.
Câu 3 (3 điểm)
Cách giải:
Cho \(\Delta ABC\) có ba góc nhọn nội tiếp đường tròn \(\left( O \right).\) Tia phân giác \(\angle BAC\) cắt cạnh \(BC\) tại \(D\) và cắt đường tròn \(\left( O \right)\) tại \(M.\) Gọi \(K\) là hình chiếu của \(M\) trên \(AB,\) \(T\) là hình chiếu của \(M\) trên \(AC.\) Chứng minh rằng:
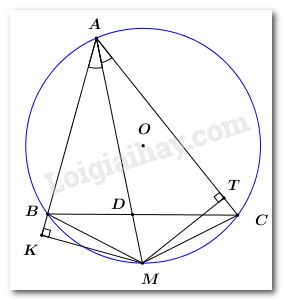
a) \(AKMT\) là tứ giác nội tiếp.
Ta có: \(\left\{ \begin{array}{l}MK \bot AB = \left\{ K \right\}\\MT \bot AC = \left\{ T \right\}\end{array} \right.\,\,\left( {gt} \right)\) \( \Rightarrow \angle AKM = \angle ATM = {90^0}\)
Xét tứ giác \(AKMT\) ta có: \(\angle AKM + \angle ATM = {90^0} + {90^0} = {180^0}\)
Mà hai góc này là hai góc đối diện
\( \Rightarrow AKMT\) là tứ giác nội tiếp (dhnb) (đpcm).
b) \(M{B^2} = M{C^2} = MD.MA.\)
Xét \(\left( O \right)\) ta có:
\(\angle MAB\) là góc nội tiếp chắn cung \(BM\)
\(\angle MAC\) là góc nội tiếp chắn cung \(CM\)
Lại có: \(MA\) là tia phân giác của \(\angle BAC\,\,\,\left( {gt} \right)\) \( \Rightarrow \angle MAB = \angle MAC.\)
\( \Rightarrow \) Số đo cung \(BM = \) Số đo cung \(CM\) (hai góc nội tiếp bằng nhau chắn hai cung bằng nhau).
Ta có:
\(\angle MBC\) là góc nội tiếp chắn cung \(MC\)
\(\angle BAM\) là góc nội tiếp chắn cung \(BM\)
\( \Rightarrow \angle MAB = \angle MBC = \angle MBD\) (hai góc nội tiếp chắn hai cung bằng nhau thì bằng nhau).
Xét \(\Delta MAB\) và \(\Delta MBD\) ta có:
\(\begin{array}{l}\angle AMB\,\,\,chung\\\angle MAB = \angle MBD\,\,\,\left( {cmt} \right)\\ \Rightarrow \Delta MAB \sim \Delta MBD\,\,\,\left( {g - g} \right)\\ \Rightarrow \dfrac{{MA}}{{MB}} = \dfrac{{MB}}{{MD}} \Rightarrow M{B^2} = MD.MA.\end{array}\)
Lại có: Số đo cung \(BM = \) Số đo cung \(CM\) (cmt) nên \(MB = MC\) (hai cung bằng nhau căng hai dây bằng nhau).
Vậy \(M{B^2} = M{C^2} = MD.MA\,\,\,\left( {dpcm} \right)\).
c) Khi đường tròn \(\left( O \right)\) và \(B,\,\,C\) cố định, điểm \(A\) thay đổi trên cung lớn \(BC\) thì tổng \(\dfrac{{AB}}{{MK}} + \dfrac{{AC}}{{MT}}\) có giá trị không đổi.
Đặt \(\angle BAM = \angle CAM = \alpha \).
Xét \(\Delta AKM\) và \(\Delta ATM\) có:
\(\begin{array}{l}AM\,\,chung\\\angle KAM = \angle TAM\,\,\left( {gt} \right)\end{array}\)
\( \Rightarrow \Delta AKM = \Delta ATM\) (cạnh huyền – góc nhọn)
\( \Rightarrow MK = MT\) (hai 2 tương ứng).
Giả sử \(AB \le AC\), khi đó ta có:
\(\begin{array}{l}\,\,\,\,\dfrac{{AB}}{{MK}} + \dfrac{{AC}}{{MT}}\\ = \dfrac{{AK - BK}}{{MK}} + \dfrac{{AT + TC}}{{MK}}\\ = \dfrac{{AK + AT - BK + TC}}{{MK}}\end{array}\)
Xét \(\Delta BMK\) và \(\Delta CMT\) có:
\(\begin{array}{l}MB = MC\,\,\left( {cmt} \right)\\MK = MT\,\,\left( {cmt} \right)\end{array}\)
\( \Rightarrow \Delta BMK = \Delta CMT\) (cạnh huyền – cạnh góc vuông)
\( \Rightarrow BK = TC\) (2 cạnh tương ứng).
\( \Rightarrow \dfrac{{AB}}{{MK}} + \dfrac{{AC}}{{MT}} = \dfrac{{AK + AT}}{{MK}}\).
Xét tam giác \(AKM\) vuông tại \(K\) có: \(AK = AM.\cos \alpha \), \(MK = AM.\sin \alpha \).
Xét tam giác \(AMT\) vuông tại \(T\) có: \(AT = AM.\cos \alpha \).
\( \Rightarrow \dfrac{{AB}}{{MK}} + \dfrac{{AC}}{{MT}} = \dfrac{{AM.\cos \alpha + AM.\cos \alpha }}{{AM.\sin \alpha }} = \dfrac{{2AM.\cos \alpha }}{{AM.\sin \alpha }} = 2\cot \alpha \).
Vì đường tròn \(\left( O \right)\) và \(BC\) cố định nên số đo cung \(BC\) không đổi.
\( \Rightarrow \angle BAC = 2\alpha = \dfrac{1}{2}\) số đo cung BC không đổi (góc nội tiếp bằng nửa số đo cung bị chắn).
\( \Rightarrow \alpha \) không đổi \( \Rightarrow 2\cot \alpha \) không đổi.
Vậy \(\dfrac{{AB}}{{MK}} + \dfrac{{AC}}{{MT}} = 2\cot \alpha \) không đổi, với \(\alpha = \dfrac{1}{4}\) số đo cung BC không đổi.
Câu 4 (1,0 điểm)
Cách giải: :
Giải phương trình \(\sqrt {{x^2} + 3x} + \sqrt {9x + 18} = 3x + \sqrt {x + \dfrac{6}{x} + 5} \)
ĐK: \(\left\{ \begin{array}{l}{x^2} + 3x \ge 0\\9x + 18 \ge 0\\x + \dfrac{6}{x} + 5 \ge 0\\x \ne 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x \ge 0,x \le - 3\\x \ge - 2\\\dfrac{{{x^2} + 5x + 6}}{x} \ge 0\\x \ne 0\end{array} \right. \Leftrightarrow x > 0\)
Khi đó
\(\begin{array}{l}PT \Leftrightarrow \sqrt {x\left( {x + 3} \right)} + 3\sqrt {x + 2} = 3x + \sqrt {\dfrac{{{x^2} + 5x + 6}}{x}} \\\,\,\,\,\,\,\, \Leftrightarrow \sqrt x \sqrt {x\left( {x + 3} \right)} + 3\sqrt x \sqrt {x + 2} = 3x\sqrt x + \sqrt {{x^2} + 5x + 6} \\\,\,\,\,\,\,\, \Leftrightarrow x\sqrt {x + 3} + 3\sqrt x \sqrt {x + 2} = 3x\sqrt x + \sqrt {\left( {x + 2} \right)\left( {x + 3} \right)} \\\,\,\,\,\,\,\, \Leftrightarrow x\sqrt {x + 3} - \sqrt {\left( {x + 2} \right)\left( {x + 3} \right)} + 3\sqrt x \sqrt {x + 2} - 3x\sqrt x = 0\\\,\,\,\,\,\,\, \Leftrightarrow \sqrt {x + 3} \left( {x - \sqrt {x + 2} } \right) - 3\sqrt x \left( {x - \sqrt {x + 2} } \right) = 0\\\,\,\,\,\,\,\, \Leftrightarrow \left( {x - \sqrt {x + 2} } \right)\left( {\sqrt {x + 3} - 3\sqrt x } \right) = 0\\\,\,\,\,\,\,\, \Leftrightarrow \left[ \begin{array}{l}x - \sqrt {x + 2} = 0\,\,\,\,\,\,\,\,\,\,\left( 1 \right)\\\sqrt {x + 3} - 3\sqrt x = 0\,\,\,\,\left( 2 \right)\end{array} \right.\end{array}\)
Ta có:
\(\begin{array}{l}\left( 1 \right) \Leftrightarrow x = \sqrt {x + 2} \Leftrightarrow {x^2} = x + 2\,\,\left( {Do\,\,x > 0} \right)\\\,\,\,\,\,\, \Leftrightarrow {x^2} - x - 2 = 0 \Leftrightarrow {x^2} + x - 2x - 2 = 0\\\,\,\,\,\,\, \Leftrightarrow x\left( {x + 1} \right) - 2\left( {x + 1} \right) = 0 \Leftrightarrow \left( {x + 1} \right)\left( {x - 2} \right) = 0\\\,\,\,\,\,\, \Leftrightarrow \left[ \begin{array}{l}x + 1 = 0\\x - 2 = 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = - 1\,\,\,\left( {KTM} \right)\\x = 2\,\,\,\,\,\,\left( {TM} \right)\end{array} \right.\end{array}\)
\(\begin{array}{l}\left( 2 \right) \Leftrightarrow \sqrt {x + 3} = 3\sqrt x \\\,\,\,\,\,\,\, \Leftrightarrow x + 3 = 9x \Leftrightarrow 3 = 8x \Leftrightarrow x = \dfrac{3}{8}\,\,\,\,\left( {TM} \right)\end{array}\)
Vậy phương trình có tập nghiệm \(S = \left\{ {2;\dfrac{3}{8}} \right\}\).