Đề thi vào 10 môn Toán Quảng Ninh năm 2020 — Không quảng cáo

Đề bài

Câu 1:

1. Thực hiện phép tính $2 + \sqrt 9 .$

2. Rút gọn biểu thức $B = \left( {\dfrac{1}{{\sqrt x  + 2}} - \dfrac{1}{{\sqrt x  + 7}}} \right):\dfrac{5}{{\sqrt x  + 7}}$ với $x \ge 0.$

3. Giải hệ phương trình $\left\{ \begin{array}{l}x + 2y = 4\\x - 2y = 0\end{array} \right..$

Câu 2:

Cho phương trình ${x^2} + 4x + 3m - 2 = 0$, với $m$ là tham số.

1. Giải phương trình với $m =  - 1$.

2. Tìm giá trị của $m$ để phương trình đã cho có một nghiệm $x = 2$.

3. Tìm giá trị của $m$ để phương trình đã cho có hai nghiệm phân biệt ${x_1},\,\,{x_2}$ sao cho ${x_1} + 2{x_2} = 1$.

Câu 3:

Khoảng cách giữa hai bến sông A và B là 32 km. Một canô xuôi dòng từ bến A đến bến B rồi lập tức quay về bến A. Kể từ lúc khởi hành đến lúc về tới bến A hết tất cả 6 giờ. Tính vận tốc của canô khi nước yên lặng biết vận tốc của dòng nước là 4 km/h.

Câu 4:

Cho đường tròn $\left( {O;R} \right)$ và $A$ là một điểm nằm bên ngoài đường tròn. Từ điểm A kẻ hai tiếp tuyến $AB$ và $AC$ với đường tròn $\left( O \right)$ ( B và C là hai tiếp điểm). Gọi $H$ là giao điểm của $AO$ và $BC$. Kẻ đường kính $BD$ của đường tròn $\left( O \right)$, $AD$ cắt đường tròn tại điểm thứ hai là $E$.

a. Chứng minh $ABOC$ là tứ giác nội tiếp

b. Tính độ dài $AH$ biết $R = 3cm,AB = 4cm.$

c. Chứng minh $AE.AD = AH.AO$

d. Tia $CE$ cắt $AH$ tại $F$. Chứng tỏ $F$ là trung điểm của $AH.$

Câu 5:

Cho $x,\,\,y$ là các số thực dương thỏa mãn $x + y \le 3$. Tìm giá trị nhỏ nhất của biểu thức

$Q = {x^2} + {y^2} - 9x - 12y + \dfrac{{16}}{{2x + y}} + 25$

Lời giải chi tiết

Câu 1 (2 điểm)

Cách giải:

1. Thực hiện phép tính $2 + \sqrt 9 .$

Ta có: $2 + \sqrt 9  = 2 + 3 = 5.$

2. Rút gọn biểu thức $B = \left( {\dfrac{1}{{\sqrt x  + 2}} - \dfrac{1}{{\sqrt x  + 7}}} \right):\dfrac{5}{{\sqrt x  + 7}}$ với $x \ge 0.$

Điều kiện: $x \ge 0$

$\begin{array}{l}B = \left( {\dfrac{1}{{\sqrt x  + 2}} - \dfrac{1}{{\sqrt x  + 7}}} \right):\dfrac{5}{{\sqrt x  + 7}}\\\,\,\,\, = \dfrac{{\sqrt x  + 7 - \sqrt x  - 2}}{{\left( {\sqrt x  + 2} \right)\left( {\sqrt x  + 7} \right)}}.\dfrac{{\sqrt x  + 7}}{5}\\\,\,\,\, = \dfrac{5}{{\left( {\sqrt x  + 2} \right)\left( {\sqrt x  + 7} \right)}}.\dfrac{{\sqrt x  + 7}}{5}\\\,\,\, = \dfrac{1}{{\sqrt x  + 2}}.\end{array}$

Vậy $B = \dfrac{1}{{\sqrt x  + 2}}$ với $x \ge 2.$

3. Giải hệ phương trình $\left\{ \begin{array}{l}x + 2y = 4\\x - 2y = 0\end{array} \right..$

$\left\{ \begin{array}{l}x + 2y = 4\\x - 2y = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}2x = 4\\x = 2y\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 2\\y = 1\end{array} \right..$

Vậy hệ phương trình có nghiệm duy nhất $\left( {x;\,\,y} \right) = \left( {2;\,\,1} \right).$

Câu 2 (2,0 điểm)

Cách giải:

Cho phương trình ${x^2} + 4x + 3m - 2 = 0$ , với $m$ là tham số.

1. Giải phương trình với $m =  - 1$ .

Thay $m =  - 1$ vào phương trình đã cho ta có:

$\begin{array}{l}\,\,\,\,\,\,\,{x^2} + 4x - 5 = 0\\ \Leftrightarrow {x^2} - x + 5x - 5 = 0\\ \Leftrightarrow x\left( {x - 1} \right) + 5\left( {x - 1} \right) = 0\\ \Leftrightarrow \left( {x - 1} \right)\left( {x + 5} \right) = 0\\ \Leftrightarrow \left[ \begin{array}{l}x - 1 = 0\\x + 5 = 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = 1\\x =  - 5\end{array} \right.\end{array}$

Vậy khi $m =  - 1$ thì tập nghiệm của phương trình là $S = \left\{ {1; - 5} \right\}$.

2. Tìm giá trị của $m$ để phương trình đã cho có một nghiệm $x = 2$ .

Vì $x = 2$ là một nghiệm của phương trình nên thay $x = 2$ vào phương trình ta có:

$\begin{array}{l}\,\,\,\,\,\,{2^2} + 4.2 + 3m - 2 = 0\\ \Leftrightarrow 3m + 10 = 0\\ \Leftrightarrow m =  - \dfrac{{10}}{3}\end{array}$

Vậy khi $m =  - \dfrac{{10}}{3}$ thì phương trình đã cho có một nghiệm $x = 2$.

3. Tìm giá trị của $m$ để phương trình đã cho có hai nghiệm phân biệt ${x_1},\,\,{x_2}$ sao cho ${x_1} + 2{x_2} = 1$ .

Ta có: $\Delta ' = {\left( { - 2} \right)^2} - \left( {3m - 2} \right) = 4 - 3m + 2 = 6 - 3m$.

Để phương trình đã cho có 2 nghiệm phân biệt ${x_1},\,\,{x_2}$ thì $\Delta ' > 0 \Leftrightarrow 6 - 3m > 0 \Leftrightarrow m < 2$.

Khi đó áp dụng định lí Vi-ét ta có: $\left\{ \begin{array}{l}{x_1} + {x_2} =  - 4\\{x_1}{x_2} = 3m - 2\end{array} \right.\,\,\left( * \right)$.

Theo bài ra ta có: ${x_1} + 2{x_2} = 1 \Leftrightarrow {x_1} = 1 - 2{x_2}$.

Thế vào hệ (*) ta có:

$\begin{array}{l}\,\,\,\,\,\,\left\{ \begin{array}{l}1 - 2{x_2} + {x_2} =  - 4\\\left( {1 - 2{x_2}} \right).{x_2} = 3m - 2\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{x_2} = 5\\\left( {1 - 2.5} \right).5 = 3m - 2\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}{x_2} = 5\\3m - 2 =  - 45\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{x_2} = 5\\m =  - \dfrac{{43}}{3}\,\,\,\left( {tm} \right)\end{array} \right.\end{array}$

Vậy $m =  - \dfrac{{43}}{3}$.

Câu 3 (2 điểm)

Cách giải:

Khoảng cách giữa hai bến sông A và B là 32 km. Một canô xuôi dòng từ bến A đến bến B rồi lập tức quay về bến A. Kể từ lúc khởi hành đến lúc về tới bến A hết tất cả 6 giờ. Tính vận tốc của canô khi nước yên lặng biết vận tốc của dòng nước là 4 km/h.

Gọi vận tốc của canô khi nước yên lặng là $x$ (km/h) $\left( {x > 4} \right)$

Vận tốc canô khi xuôi dòng là $x + 4$ (km/h)

Vận tốc canô khi ngược dòng là $x - 4$ (km/h)

Thời gian canô xuôi dòng từ bến A đến bến B là $\dfrac{{32}}{{x + 4}}$ giờ

Thời gian canô ngược dòng từ bến B về bến A là $\dfrac{{32}}{{x - 4}}$ giờ

Vì từ lúc khởi hành đến lúc về tới bến A hết tất cả 6 giờ nên ta có phương trình:

$\begin{array}{l}\dfrac{{32}}{{x + 4}} + \dfrac{{32}}{{x - 4}} = 6\\ \Leftrightarrow \dfrac{{32\left( {x - 4} \right) + 32\left( {x + 4} \right)}}{{\left( {x - 4} \right)\left( {x + 4} \right)}} = 6\\ \Leftrightarrow \dfrac{{32x - 128 + 32x + 128}}{{\left( {x - 4} \right)\left( {x + 4} \right)}} = 6\\ \Leftrightarrow \dfrac{{64x}}{{{x^2} - 16}} = 6\\ \Rightarrow 6{x^2} - 96 = 64x\\ \Leftrightarrow 6{x^2} - 64x - 96 = 0\\ \Leftrightarrow 3{x^2} - 32x - 48 = 0\\ \Leftrightarrow 3{x^2} - 36x + 4x - 48 = 0\\ \Leftrightarrow 3x\left( {x - 12} \right) + 4\left( {x - 12} \right) = 0\\ \Leftrightarrow \left( {3x + 4} \right)\left( {x - 12} \right) = 0\\ \Leftrightarrow \left[ \begin{array}{l}3x + 4 = 0\\x - 12 = 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x =  - \dfrac{4}{3}\,\,\left( {ktm} \right)\\x = 12\,\,\,\left( {tm} \right)\end{array} \right.\end{array}$

Vậy vận tốc của canô khi nước yên lặng là 12 km/h.

Câu 4 (3,5 điểm)

Cách giải:

Cho đường tròn $\left( {O;R} \right)$ và $A$ là một điểm nằm bên ngoài đường tròn. Từ điểm A kẻ hai tiếp tuyến $AB$ và $AC$ với đường tròn $\left( O \right)$ ( B và C là hai tiếp điểm). Gọi $H$ là giao điểm của $AO$ và $BC$ . Kẻ đường kính $BD$ của đường tròn $\left( O \right)$ , $AD$ cắt đường tròn tại điểm thứ hai là $E$ .

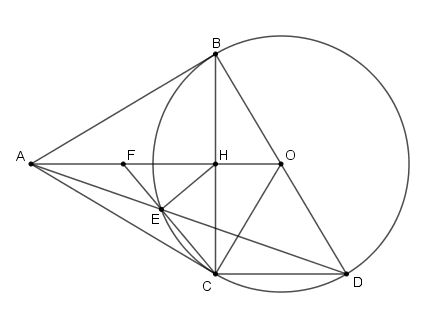
a. Chứng minh $ABOC$ là tứ giác nội tiếp

Xét đường tròn $\left( O \right)$ có $AB$ và $AC$ là các tiếp tuyến, $B,C$ là các tiếp điểm tương ứng nên $\angle ABO = {90^0};\angle ACO = {90^0}$

Xét tứ giác $ABOC$ có $\angle ABO + \angle ACO = {90^0} + {90^0} = {180^0}$ mà hai góc $\angle ABO;\angle ACO$ đối nhau nên tứ giác $ABOC$ là tứ giác nội tiếp (dhnb)

b. Tính độ dài $AH$ biết $R = 3cm,AB = 4cm.$

Xét đường tròn $\left( O \right)$ có $AB$ và $AC$ là hai tiếp tuyến cắt nhau tại $A.$

Suy ra $AB = AC$ (tính chất), mà $OB = OC = R$ nên $AO$ là đường trung trực của đoạn $BC$

Do đó $OA \bot BC$ tại $H.$

Xét tam giác $ABO$ vuông tại $B$, theo định lý Pytago ta có: $A{O^2} = A{B^2} + O{B^2} = {4^2} + {3^2} = 25$ $\Rightarrow OA = 5cm$

Xét tam giác $ABO$ vuông tại $B$ có $BH$ là đường cao, theo hệ thức lượng trong tam giác vuông ta có: $A{B^2} = AH.AO$$\Leftrightarrow AH = \dfrac{{A{B^2}}}{{AO}} = \dfrac{{{4^2}}}{5} = 3,2cm$

Vậy $AH = 3,2cm$.

c. Chứng minh $AE.AD = AH.AO$

Xét tam giác $ABO$ vuông tại $B$ có $BH$ là đường cao, theo hệ thức lượng trong tam giác vuông ta có: $A{B^2} = AH.AO$ (1)

Xét tam giác $AEB$ và tam giác $ABD$ có:

$\angle BAE$ chung

$\angle ABE = \angle BDE$ (góc nội tiếp và góc tạo bởi tiếp tuyến và dây cung cùng chắn cung $BE$ trong đường tròn $\left( O \right)$)

Suy ra $\Delta AEB \sim \Delta ABD\left( {g - g} \right)$

$\Rightarrow \dfrac{{AE}}{{AB}} = \dfrac{{AB}}{{AD}} \Rightarrow AE.AD = A{B^2}$ (2)

Từ (1) và (2) suy ra $AE.AD = AH.AO$.

d. Tia $CE$ cắt $AH$ tại $F$ . Chứng tỏ $F$ là trung điểm của $AH.$

Xét đường tròn $\left( O \right)$ có $\angle BCD = {90^0}$ (góc nội tiếp chắn nửa đường tròn), suy ra $BC \bot CD$

Lại có $AO \bot BC$ nên $CD//AO$

Suy ra $\angle ADC = \angle OAD$ (so le trong)

Xét $\left( O \right)$ có $\angle ACE = \angle EDC$ (góc nội tiếp và góc tạo bởi tiếp tuyến và dây cung cùng chắn cung $EC$)

Suy ra $\angle ACE = \angle FAE$ $\left( { = \angle CDE} \right)$

Xét $\Delta AFE$ và $\Delta CFA$ có:

$\angle AFE$ chung

$\angle ACE = \angle FAE$ (cmt)

Suy ra $\Delta AFE \sim \Delta CFA\left( {g - g} \right)$

$\begin{array}{l} \Rightarrow \dfrac{{AF}}{{CF}} = \dfrac{{FE}}{{FA}}\\ \Rightarrow F{A^2} = FC.FE\left( * \right)\end{array}$

Theo câu b ta có $AE.AD = AH.AO$$\Rightarrow \dfrac{{AE}}{{AH}} = \dfrac{{AO}}{{AD}}$

Suy ra $\Delta AEH \sim \Delta AOD\left( {c - g - c} \right)$ $\Rightarrow \angle AHE = \angle ADO$

Suy ra tứ giác $EHOD$ là tứ giác nội tiếp (góc ngoài tại 1 đỉnh bằng góc trong tại đỉnh đối với đỉnh đó)

Suy ra $\angle HED = \angle BOA$ (cùng phụ với $\angle AOD$)

Xét đường tròn $\left( O \right)$ có $\angle CED = \angle CBD$ (2 góc nội tiếp cùng chắn cung $CD$)

Lại có $\angle BOH + \angle HBO = {90^0}$ (do $\Delta BHO$ vuông tại $H$)

Nên $\angle EHD + \angle CED = {90^0} \Rightarrow \angle HEC = {90^0}$  hay $EH \bot FC$

Xét tam giác $HFC$ vuông tại H có $HE$ là đường cao, theo hệ thức lượng trong tam giác vuông ta có:

$F{H^2} = FE.FC$ (**)

Từ (*) và (**) suy ra $F{A^2} = F{H^2}$ $\Leftrightarrow FA = FH \Rightarrow F$ là trung điểm $AH$.

Câu 5 (0,5 điểm)

Cách giải:

Cho $x,y$ là các số thực dương thỏa mãn $x + y \le 3$ . Tìm giá trị nhỏ nhất của biểu thức

$Q = {x^2} + {y^2} - 9x - 12y + \dfrac{{16}}{{2x + y}} + 25$

Ta có:

$\begin{array}{l}Q = {x^2} + {y^2} - 9x - 12y + \dfrac{{16}}{{2x + y}} + 25\\ = \left( {{x^2} - 2x + 1} \right) + \left( {{y^2} - 4y + 4} \right) + \left( {2x + y} \right) + \dfrac{{16}}{{2x + y}} - 9\left( {x + y} \right) + 20\\ = {\left( {x - 1} \right)^2} + {\left( {y - 2} \right)^2} + \left( {2x + y} \right) + \dfrac{{16}}{{2x + y}} - 9\left( {x + y} \right) + 20\end{array}$

$\begin{array}{l}{\left( {x - 1} \right)^2} \ge 0\\{\left( {y - 2} \right)^2} \ge 0\\2x + y + \dfrac{{16}}{{2x + y}} \ge 2\sqrt {\left( {2x + y} \right).\dfrac{{16}}{{2x + y}}}  = 8\\ - 9\left( {x + y} \right) \ge  - 9.3 =  - 27\\ \Rightarrow Q \ge 0 + 0 + 8 - 27 + 20 = 1\\ \Rightarrow Q \ge 1\end{array}$

Dấu “=” xảy ra khi $x = 1,y = 2$.

Vậy ${Q_{\min }} = 1$ khi $x = 1,y = 2$.