Đề thi vào 10 môn Toán Quảng Trị năm 2019 — Không quảng cáo

Đề bài

Câu 1 (2,0 điểm):

Bằng các phép biến đổi đại số, hãy rút gọn các biểu thức sau:

\(A = \sqrt {18}  - \sqrt {50} \)

\(B = \left( {\dfrac{1}{{\sqrt a  - 2}} + \dfrac{1}{{\sqrt a  + 2}}} \right).\dfrac{{a - 4}}{{\sqrt a }}\) với \(a > 0,\,a \ne 4\)

Câu 2 (2,5 điểm): Cho hàm số \(y =  - {x^2}\) có đồ thị \(\left( P \right)\).

a) Vẽ \(\left( P \right)\)

b) Tìm tọa độ giao điểm của \(\left( P \right)\) và đường thẳng \(\left( {{d_1}} \right):y = 2x - 3\).

c) Tìm tất cả các giá trị của tham số \(m\) để đường thẳng \(\left( {{d_2}} \right)\): \(y = 2x + m\) cắt \(\left( P \right)\) tại hai điểm phân biệt có hoành độ \({x_1}\) và \({x_2}\) thỏa mãn \(\dfrac{1}{{{x_1}}} + \dfrac{1}{{{x_2}}} = \dfrac{2}{5}\).

Câu 3 (1,5 điểm): Một mảnh đất hình chữ nhật có chu vi là \(58m\) và diện tích là \(190{m^2}\) . Tính chiều dài và chiều rộng mảnh đất đó.

Câu 4 (3 điểm): Từ điểm \(M\) nằm ngoài đường tròn \(\left( O \right),\) kẻ đến \(\left( O \right)\) các tiếp tuyến \(MP,MQ\) và cát tuyến \(MAB\) không đi qua tâm (\(A,B,P,Q\)  thuộc \(\left( O \right)\)). Gọi \(I\) là trung điểm của \(AB,\) \(E\) là giao điểm của \(PQ\) và \(AB.\)

a) Chứng minh \(MPOQ\) là tứ giác nội tiếp

b) Chứng minh hai tam giác \(MPE\) và \(MIP\) đồng dạng với nhau.

c) Giả sử \(PB = a\) và \(A\) là trung điểm của \(MB.\) Tính \(PA\) theo \(a.\)

Câu 5 (1 điểm): Giải phương trình \(\sqrt {2x - 4}  + \sqrt {6 - 2x}  = 4{x^2} - 20x + 27\)

Lời giải

Câu 1 (VD)

Phương pháp:

Sử dụng công thức: \(\sqrt {{A^2}B}  = \left| A \right|\sqrt B  = \left\{ \begin{array}{l}A\sqrt B \,\,\,khi\,\,A \ge 0\\ - A\sqrt B \,\,\,khi\,\,\,\,A < 0\end{array} \right..\)

Cách giải:

\(A = \sqrt {18}  - \sqrt {50}  = \sqrt {9.2}  - \sqrt {25.2}  = 3\sqrt 2  - 5\sqrt 2  =  - 2\sqrt 2 \)

Với \(a > 0,\,\,a \ne 4\) ta có:

\(\begin{array}{l}B = \left( {\dfrac{1}{{\sqrt a  - 2}} + \dfrac{1}{{\sqrt a  + 2}}} \right).\dfrac{{a - 4}}{{\sqrt a }} = \left( {\dfrac{{\sqrt a  + 2}}{{a - 4}} + \dfrac{{\sqrt a  - 2}}{{a - 4}}} \right).\dfrac{{a - 4}}{{\sqrt a }}\\\,\,\,\, = \dfrac{{2\sqrt a }}{{a - 4}}.\dfrac{{a - 4}}{{\sqrt a }} = 2.\end{array}\)

Vậy \(A =  - 2\sqrt 2 \) và \(B = 2\).

Câu 2 (VD):

Phương pháp:

a) Tìm các điểm đi qua của Parabol và vẽ đồ thị hàm số.

b) Xét phương trình hoành độ giao điểm, giải phương trình tìm \(x\) và suy ra \(y\). Từ đó kết luận giao điểm.

c) Phương trình có hai nghiệm phân biệt khác \(0\) \( \Leftrightarrow \Delta ' > 0\) và \(x = 0\) không là nghiệm của phương trình.

Biến đổi điều kiện bài cho làm xuất hiện \({x_1} + {x_2}\) và \({x_1}{x_2}\) rồi áp dụng Vi – et tìm \(m\).

Kiểm tra điều kiện của \(m\) và kết luận.

Cách giải:

a) Vẽ \(\left( P \right)\)

Cho \(x\) nhận các giá trị \( - 2; - 1;0;1;2\) ta có bảng sau:

Do đó đồ thị hàm số đi qua các điểm \(A\left( { - 2; - 4} \right),B\left( { - 1; - 1} \right),O\left( {0;0} \right),C\left( {1; - 1} \right),D\left( {2; - 4} \right)\).

Đồ thị:

b) Tìm tọa độ giao điểm của \(\left( P \right)\) và đường thẳng \(\left( {{d_1}} \right):y = 2x - 3\) .

Xét phương trình hoành độ giao điểm của parabol \(\left( P \right)\) và đường thẳng \(\left( {{d_1}} \right)\):

\( - {x^2} = 2x - 3 \Leftrightarrow {x^2} + 2x - 3 = 0 \Leftrightarrow \left[ \begin{array}{l}x = 1\\x =  - 3\end{array} \right.\)

Với \(x = 1\) thì \(y =  - 1\) nên \(E\left( {1; - 1} \right)\)

Với \(x =  - 3\) thì \(y =  - 9\) nên \(F\left( { - 3; - 9} \right)\)

Vậy giao điểm của \(\left( P \right)\) và \(\left( {{d_1}} \right)\) lần lượt là \(E\left( {1; - 1} \right)\) và \(F\left( { - 3; - 9} \right)\).

c) Tìm tất cả các giá trị của tham số \(m\) để đường thẳng \(\left( {{d_2}} \right)\) : \(y = 2x + m\) cắt \(\left( P \right)\) tại hai điểm phân biệt có hoành độ \({x_1}\) và \({x_2}\) thỏa mãn \(\dfrac{1}{{{x_1}}} + \dfrac{1}{{{x_2}}} = \dfrac{2}{5}\) .

Xét phương trình hoành độ giao điểm của \(\left( P \right)\) và \(\left( {{d_2}} \right)\) là:

\( - {x^2} = 2x + m \Leftrightarrow {x^2} + 2x + m = 0\,\,\left( 1 \right)\)

Để \(\left( P \right)\) và \(\left( {{d_2}} \right)\) cắt nhau tại hai điểm phân biệt thì \(\Delta ' > 0 \Leftrightarrow 1 - m > 0 \Leftrightarrow m < 1\).

Từ yêu cầu bài toán ta suy ra \({x_1},{x_2} \ne 0\) nên  phương trình \(\left( 1 \right)\) không nhận \(x = 0\) làm nghiệm hay\({0^2} + 2.0 + m \ne 0 \Leftrightarrow m \ne 0\).

Theo hệ thức Vi – et ta có: \(\left\{ \begin{array}{l}{x_1} + {x_2} =  - 2\\{x_1}{x_2} = m\end{array} \right.\).

Khi đó:

\(\begin{array}{l}\dfrac{1}{{{x_1}}} + \dfrac{1}{{{x_2}}} = \dfrac{2}{5} \Leftrightarrow \dfrac{{{x_1} + {x_2}}}{{{x_1}{x_2}}} = \dfrac{2}{5}\\ \Rightarrow 5\left( {{x_1} + {x_2}} \right) = 2{x_1}{x_2}\\ \Rightarrow 5.\left( { - 2} \right) = 2.m \Leftrightarrow m =  - 5\left( {TM} \right)\end{array}\)

Vậy \(m =  - 5\) là giá trị cần tìm.

Câu 3 (VD):

Phương pháp:

Bước 1: Lập phương trình

- Chọn ẩn số và đặt điều kiện thích hợp cho ẩn số.

- Biểu diễn các đại lượng chưa biết theo ẩn và các đại lượng đã biết

- Lập phương trình biểu thị mối quan hệ giữa các đại lượng.

Bước 2. Giải phương trình

Bước 3: Trả lời

Kiểm tra xem trong các nghiệm của phương trình, nghiệm nào thoả mãn điều kiện của ẩn, nghiệm nào không, rồi kết luận.

Cách giải:

Gọi chiều rộng mảnh đất hình chữ nhật là \(x\,\left( m \right)\);

chiều dài mảnh đất hình chữ nhật là \(y\left( m \right)\).

Điều kiện: \(y > x > 0\).

Nửa chu vi mảnh đất hình chữ nhật là : \(58:2 = 29\left( m \right)\) nên \(x + y = 29\).

Diện tích mảnh đất hình chữ nhật là \(190{m^2}\) nên: \(x.y = 190\).

Theo bài ra ta có hệ phương trình \(\left\{ \begin{array}{l}x + y = 29\\xy = 190\end{array} \right.\)

Khi đó \(x,y\) là nghiệm của phương trình:

\({X^2} - 29X + 190 = 0 \Leftrightarrow \left( {X - 19} \right)\left( {X - 10} \right) = 0 \Leftrightarrow \left[ \begin{array}{l}X = 19\,\,\,(tm)\\X = 10\,\,\,\,\left( {tm} \right)\end{array} \right.\,\)

Vì \(x < y\) nên : \(x = 10;\,y = 19\)

Vậy chiều rộng mảnh đất là \(10m;\) chiều dài mảnh đất là \(19m\) .

Câu 4 (VD):

Phương pháp:

a) Chỉ ra tứ giác có tổng hai góc đối bằng \(180^\circ \) là tứ giác nội tiếp

b) Chứng minh hai tam giác đồng dạng theo trường hợp góc –góc

c) Chứng minh hai tam giác \(MAP\) và \(MPB\) đồng dạng từ đó suy ra tỉ lệ cạnh và tính \(PA.\)

Cách giải:

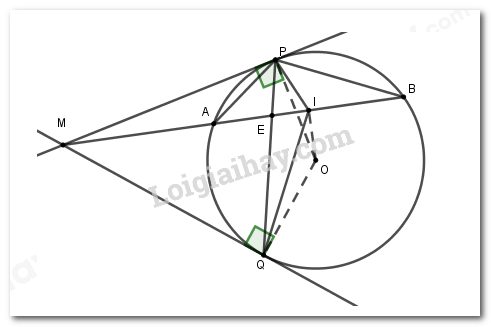
a) Chứng minh \(MPOQ\) là tứ giác nội tiếp

Vì \(MP,MQ\) là hai tiếp tuyến của \(\left( O \right)\) nên \(MP \bot OP;\,MQ \bot OQ \Rightarrow \angle MPO = 90^\circ ;\,\angle MQO = 90^\circ \)

Xét tứ giác \(MPOQ\) có \(\angle MPO + \angle MQO = 90^\circ  + 90^\circ  = 180^\circ \) mà hai góc ở vị trí đối nhau nên tứ giác \(MPOQ\) là tứ giác nội tiếp.

b) Chứng minh hai tam giác \(MPE\) và \(MIP\) đồng dạng với nhau.

Xét \(\left( O \right)\) có \(AB\) là dây và \(I\) là trung điểm \(AB\) nên \(OI \bot AB\) tại \(I\) (quan hệ giữa đường kính và dây)

Ta có \(\angle MPO = 90^\circ ;\,\angle MQO = 90^\circ ;\,\angle MIO = 90^\circ \) nên 5 điểm \(M;P;Q;I;O\) cùng thuộc đường tròn đường kính \(MO.\)

Suy ra \(\angle MIP = \angle MPQ\) (góc nội tiếp cùng chắn cung \(MP\)) (1)

Ta lại có \(MP = MQ\) (tính chất hai tiếp tuyến cắt nhau) nên \(\Delta MPQ\) cân tại \(M \Rightarrow \angle MPQ = \angle MQP\) (2)

Từ (1) và (2) suy ra \(\angle MIP = \angle MPE\)

Xét \(\Delta MPE\) và \(\Delta MIP\) có \(\angle PMI\) chung và \(\angle MIP = \angle MPE\) (cmt) nên \(\Delta MPE \sim \Delta MIP\left( {g - g} \right)\)

c) Giả sử \(PB = a\) và \(A\) là trung điểm của \(MB.\) Tính \(PA\) theo \(a.\)

Xét đường tròn \(\left( O \right)\) có \(\angle MPA = \angle MBP\) (góc tạo bởi tiếp tuyến và dây cung và góc nội tiếp cùng chắn cung \(AP\))

Xét \(\Delta MPA\) và \(\Delta MBP\) có \(\angle PMB\) chung và \(\angle MPA = \angle MBP\) (cmt)

Suy ra \(\dfrac{{MA}}{{MP}} = \dfrac{{MP}}{{MB}} = \dfrac{{AP}}{{PB}}\)

\( \Rightarrow M{P^2} = MA.MB\) mà \(A\) là trung điểm của \(MB\) nên \(MB = 2MA\)

Do đó, \(M{P^2} = MA.2MA \Leftrightarrow M{P^2} = 2M{A^2} \Leftrightarrow MP = \sqrt 2 MA \Leftrightarrow \dfrac{{MA}}{{MP}} = \dfrac{1}{{\sqrt 2 }}\)

Suy ra \(\dfrac{{AP}}{{PB}} = \dfrac{{MA}}{{MP}} = \dfrac{1}{{\sqrt 2 }} \Leftrightarrow AP = \dfrac{{PB}}{{\sqrt 2 }} = \dfrac{{a\sqrt 2 }}{2}.\)

Vậy \(AP = \dfrac{{a\sqrt 2 }}{2}.\)

Câu 5 (VDC):

Phương pháp:

- Tìm ĐKXĐ.

- Đặt ẩn phụ \(\sqrt {2x - 4}  + \sqrt {6 - 2x}  = t\) và tìm điều kiện.

- Đưa phương trình về phương trình ẩn \(t\).

- Giải phương trình ẩn \(t\) tìm \(t\) và suy ra \(x\).

Cách giải:

Điều kiện: \(\left\{ \begin{array}{l}2x - 4 \ge 0\\6 - 2x \le 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x \ge 2\\x \le 3\end{array} \right. \Leftrightarrow 2 \le x \le 3\)

Đặt \(\sqrt {2x - 4}  + \sqrt {6 - 2x}  = t\left( {t \ge 0} \right)\) ta có:

\(\begin{array}{l}{t^2} = {\left( {\sqrt {2x - 4}  + \sqrt {6 - 2x} } \right)^2}\\ = 2x - 4 + 6 - 2x + 2\sqrt {\left( {2x - 4} \right)\left( {6 - 2x} \right)} \\ = 2 + 2\sqrt { - 4{x^2} + 20x - 24} \\ \Rightarrow \sqrt { - 4{x^2} + 20x - 24}  = \dfrac{{{t^2} - 2}}{2}.\end{array}\)

Điều kiện: \(\dfrac{{{t^2} - 2}}{2} \ge 0 \Leftrightarrow \left[ \begin{array}{l}t \ge \sqrt 2 \\t \le  - \sqrt 2 \end{array} \right.\), kết hợp \(t \ge 0\) ta được \(t \ge \sqrt 2 \).

Khi đó \( - 4{x^2} + 20x - 24 = {\left( {\dfrac{{{t^2} - 2}}{2}} \right)^2} \Leftrightarrow 4{x^2} - 20x + 24 =  - \dfrac{{{t^4} - 4{t^2} + 4}}{4}\)

Thay vào phương trình đã cho ta được:

\(\begin{array}{l}t =  - \dfrac{{{t^4} - 4{t^2} + 4}}{4} + 3 \Leftrightarrow 4t =  - {t^4} + 4{t^2} - 4 + 12 \Leftrightarrow {t^4} - 4{t^2} + 4t - 8 = 0\\ \Leftrightarrow {t^2}\left( {{t^2} - 4} \right) + 4\left( {t - 2} \right) = 0 \Leftrightarrow {t^2}\left( {t - 2} \right)\left( {t + 2} \right) + 4\left( {t - 2} \right) = 0\\ \Leftrightarrow \left( {t - 2} \right)\left[ {{t^2}\left( {t + 2} \right) + 4} \right] = 0\end{array}\)

\( \Leftrightarrow t - 2 = 0\) (do \(t \ge \sqrt 2 \) nên \({t^2}\left( {t + 2} \right) + 4 > 0,\forall t\))

\( \Leftrightarrow t = 2\left( {TM} \right)\)

Suy ra \(4{x^2} - 20x + 24 =  - 1 \Leftrightarrow 4{x^2} - 20x + 25 = 0 \Leftrightarrow x = \dfrac{5}{2}\left( {TM} \right)\)

Vậy phương trình có nghiệm \(x = \dfrac{5}{2}\).