Giải bài 1 trang 23 Chuyên đề học tập Toán 11 Cánh diều
Cho hình chữ nhật ABCD có O là giao điểm hai đường chéo. Gọi M, N lần lượt là trung điểm của AB, BC
Đề bài
Cho hình chữ nhật ABCD có O là giao điểm hai đường chéo. Gọi M, N lần lượt là trung điểm của AB, BC. Xác định phép tịnh tiến biến tam giác AMO thành tam giác ONC.
Phương pháp giải - Xem chi tiết
- Cho vectơ \(\overrightarrow u \), phép tịnh tiến theo vectơ \(\overrightarrow u \) là phép biến hình biến điểm M thành điểm M’ sao cho \(\overrightarrow {MM'} = \overrightarrow u \).
- Cần xác định vecto \(\overrightarrow u \).
Lời giải chi tiết
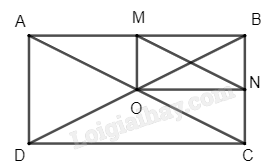
Vì O là giao điểm hai đường chéo của hình chữ nhật ABCD nên O là trung điểm của AC.
Suy ra \(\overrightarrow {AO} = \overrightarrow {OC} = \frac{1}{2}\overrightarrow {AC} \,\,(1)\)
Ta có M, N lần lượt là trung điểm của AB và BC nên MN là đường trung bình của tam giác ABC, suy ra MN // AC và \(MN = \;\frac{1}{2}AC\). Do đó, \(\overrightarrow {MN} = \frac{1}{2}\overrightarrow {AC} \,\,(2)\)
Từ (1) và (2) suy ra \(\overrightarrow {AO} = \overrightarrow {OC} = \overrightarrow {MN} \).
Khi đó, ta có phép tịnh tiến theo vectơ \(\overrightarrow {AO} \) biến các điểm A, M, O lần lượt thành các điểm O, N, C.
Vậy phép tịnh tiến theo vectơ \(\overrightarrow {AO} \) biến tam giác AMO thành tam giác ONC.