Giải bài 1 trang 32 Chuyên đề học tập Toán 11 Cánh diều
Phép biến hình nào trong các phép biến hình dưới đây là phép vị tự?
Đề bài
Phép biến hình nào trong các phép biến hình dưới đây là phép vị tự?
a) Phép tịnh tiến theo vectơ khác \(\vec 0\) ;
b) Phép đối xứng tâm;
c) Phép đối xứng trục;
d) Phép quay.
Phương pháp giải - Xem chi tiết
Nếu phép vị tự tâm O tỉ số k \(\left( {k \ne 0} \right)\) lần lượt biến 2 điểm A, B thành 2 điểm A’, B’ thì \(A'B' = \left| k \right|AB\)
Lời giải chi tiết
a) Phép tịnh tiến theo vectơ khác \(\overrightarrow 0 \) không phải là phép vị tự vì không có điểm nào biến thành chính nó.
b) Phép đối xứng tâm là phép vị tự với tâm là tâm đối xứng và tỉ số k = – 1.
Chứng minh:
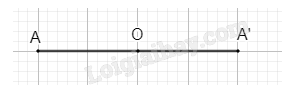
Giả sử ta có phép đối xứng tâm O biến điểm A thành điểm A', khi đó O là trung điểm của AA', suy ra \(\overrightarrow {OA'} = - \overrightarrow {OA} \), do đó ta có phép vị tự tâm O tỉ số – 1 biến điểm A thành A'.
c) Phép đối xứng trục không phải là phép vị tự vì các đường thẳng nối cặp điểm tương ứng không đồng quy.
d) Phép quay với tâm O bất kì và góc quay \(\varphi = 2k\pi \) (chính là phép đồng nhất) là phép vị tự tâm O với tỉ số \(k = 1\).
Phép quay với tâm O bất kì và góc quay \(\varphi = \left( {2k{\rm{ }} + {\rm{ }}1} \right)\pi \) (chính là phép đối xứng tâm O) là phép vị tự tâm O với tỉ số \(k = -1\).
Phép quay với góc bất kì khác \(2k\pi ,{\rm{ }}\left( {2k + 1} \right)\pi \) không phải là phép vị tự.