Giải bài 1 trang 88 SGK Toán 8 tập 1– Chân trời sáng tạo
Bạn Nam dùng 6 đoạn tre vót thẳng để làm khung diều
Đề bài
Bạn Nam dùng 6 đoạn tre vót thẳng để làm khung diều hình thoi. Trong đó có 2 đoạn tre dài 60cm và 80cm để làm hai đường chéo của cái diều, 4 đoạn tre còn lại là 4 cạnh của cái diều, Khi đó tổng độ dài 4 đoạn tre dùng làm cạnh của cái diều hình thoi là:
A. 5m
B. 1m
C. 1,5m
D. 2m
Phương pháp giải - Xem chi tiết
Áp dụng tính chất của hình thoi và ĐL Pythagore để tính độ dài cạnh hình thoi
Lời giải chi tiết
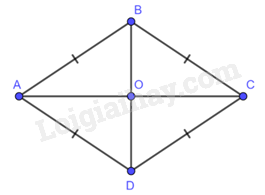
Giả sử hình thoi \(ABCD\) có hai đường chéo \(AC = 80\) cm; \(BD = 60\) cm
Suy ra:
\(BD \bot AC\) hay \(\widehat {BOA} = 90^\circ \)
\(OA = OC = \frac{1}{2}AC = \frac{1}{2}.80 = 40\) cm;
\(OB = OD = \frac{1}{2}BD = \frac{1}{2}.60 = 30\) cm
Áp dụng định lý Pythagore vào tam giác vuông \(BOA\) nên ta có:
\(A{B^2} = O{B^2} + O{A^2} = {30^2} + {40^2} = 900 + 1600 = 2500 = {50^2}\)
\(AB = 50\) (cm)
Chu vi hình thoi là: \(50.4 = 200\) (cm) \( = 2\) (m)
Tổng độ dài bốn đoạn tre dùng làm cạnh của cái diều là 2m