Giải bài 10 trang 120 vở thực hành Toán 8 tập 2
Bạn Trang cắt miếng bìa hình tam giác đều cạnh dài 20 cm và gấp lại theo các dòng kẻ (nét đứt) để được hình chóp tam giác đều.
Đề bài
Bạn Trang cắt miếng bìa hình tam giác đều cạnh dài 20 cm và gấp lại theo các dòng kẻ (nét đứt) để được hình chóp tam giác đều. Tính diện tích xung quanh của hình chóp tam giác đều tạo thành. Cho biết \(\sqrt {75} \approx 8,66\) .
Phương pháp giải - Xem chi tiết
- Các mặt bên của hình chóp là tam giác giác đều cạnh là 10 cm Ta tính được trung đoạn của hình chóp.
- Tính diện tích xung quanh của hình chóp tam giác đều
Lời giải chi tiết
Hình chóp tạo thành là hình chóp tam giác đều như hình 10.25.
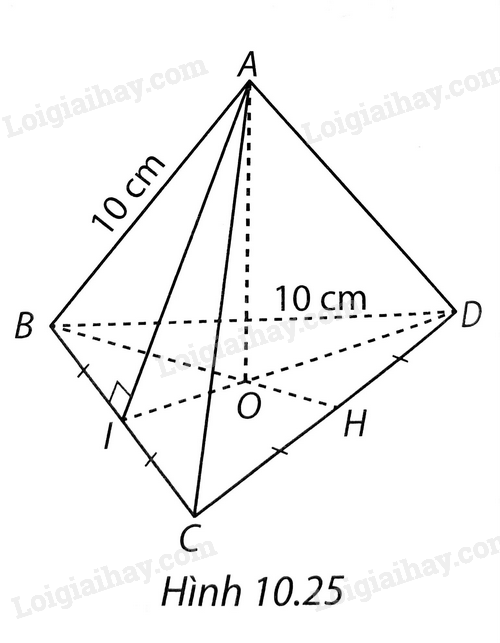
IA là trung đoạn của hình chóp.
Áp dụng định lí Pythagore cho tam giác ABI vuông tại I, ta có:
\(\begin{array}{l}B{I^2} = A{I^2} = A{B^2}\\{5^2} + A{I^2} = {10^2}\\A{I^2} = {10^2} - {5^2}\\AI = 8,66\end{array}\)
Diện tích xung quanh của hình chóp S.ABC là:
\({S_{xq}} = p.d = \frac{{10.3}}{2}.8,66 = 129,9(c{m^2})\).