Giải bài 14 trang 120 SGK Toán 7 tập 2 - Cánh diều — Không quảng cáo

Đề bài

Cho tam giác nhọn ABC có AB < AC . Hai đường cao AD và CE cắt nhau tại H . Khi đó

A.$\widehat {HAB} = \widehat {HAC}$.

B.$\widehat {HAB} > \widehat {HAC}$.

C.$\widehat {HAB} = \widehat {HCB}$.

D.$\widehat {HAC} = \widehat {BAC}$.

Lời giải chi tiết

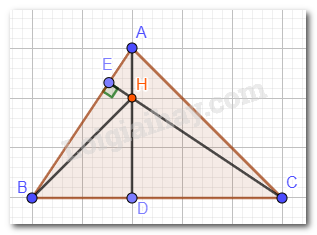
Ta có: AB < AC nên $\widehat {ACB} < \widehat {ABC}$ (góc ACB đối diện với cạnh AB ; góc ABC đối diện với cạnh AC )

Mà tam giác ADB và tam giác ADC vuông tại D .

Vì tổng hai góc nhọn trong một tam giác vuông bằng 90°.

Mà $\widehat {ACB} < \widehat {ABC}$.

Suy ra: $90^\circ  - \widehat {ACB} > 90^0 - \widehat {ABC}$ hay $\widehat {DAC} > \widehat {DAB}$.

Vậy $\widehat {HAC} > \widehat {HAB}$ hay $\widehat {HAB} < \widehat {HAC}$.

Suy ra: A, B, D sai.

Đáp án: C.$\widehat {HAB} = \widehat {HCB}$.