Giải bài 19 trang 80 SBT toán 10 - Cánh diều
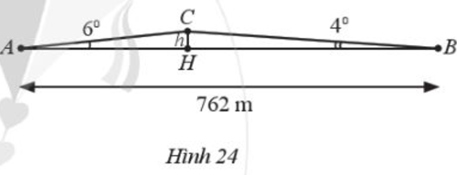
Lúc 6 giờ sáng, bạn An đi xe đạp từ nhà (điểm A) đến trường (điểm B) phải leo lên và xuống một con dốc (Hình 24). Cho biết đoạn thẳng AB dài 762 m, \(\widehat A = {6^0},\widehat B = {4^0}\)
Đề bài
Lúc 6 giờ sáng, bạn An đi xe đạp từ nhà (điểm A ) đến trường (điểm B ) phải leo lên và xuống một con dốc (Hình 24). Cho biết đoạn thẳng AB dài 762 m, \(\widehat A = {6^0},\widehat B = {4^0}\)
a) Tính chiều cao h của con dốc theo đơn vị mét (làm tròn kết quả đến hàng đơn vị)
b) Hỏi bạn An đến trường lúc mấy giờ? Biết rằng tốc độ trung bình lên dốc là 4 km/h và tốc độ trung bình khi xuống dốc là 19 km/h.
Phương pháp giải - Xem chi tiết
Bước 1: Tính số đo góc \(\widehat {ACB}\)và sử dụng định lí sin để tính độ dài AC hoặc BC
Bước 2: Sử dụng tỉ số lượng giác trong tam giác vuông để tính độ dài CH
Bước 3: Tính độ dài BC và thời gian đi quãng đường AC , BC để tìm thời điểm bạn An đến trường
Bước 4: Kết luận
Lời giải chi tiết
a) Ta có: \(\widehat {ACB} = {180^0} - (\widehat {CBA} + \widehat {CAB}) = {170^0}\)
Áp dụng định lí sin cho ∆ ABC ta có: \(\frac{{AC}}{{\sin \widehat {CBA}}} = \frac{{AB}}{{\sin \widehat {ACB}}} \Rightarrow AC = \frac{{AB.\sin \widehat {CBA}}}{{\sin \widehat {ACB}}} = \frac{{762.\sin {4^0}}}{{\sin {{170}^0}}} \approx 306\) (m)
Xét ∆ AHC vuông tại H, AC = 306 m, \(\widehat {CAH} = {6^0}\) có: \(CH = AC.\sin \widehat {CAH} = 306.\sin {6^0} \approx 32\)
Vậy chiều cao h của con dốc là 32 m
b) Áp dụng định lí sin cho ∆ ABC ta có: \(\frac{{BC}}{{\sin \widehat {BAC}}} = \frac{{AB}}{{\sin \widehat {ACB}}} \Rightarrow BC = \frac{{AB.\sin \widehat {BAC}}}{{\sin \widehat {ACB}}} = \frac{{762.\sin {6^0}}}{{\sin {{170}^0}}} \approx 459\) (m)
Ta có: \(AC \approx 0,306\) km, \(BC \approx 0,459\) km
Thời gian bạn An đi quãng đường AC là \({t_1} = \frac{{0,306}}{4}\) (giờ)
Thời gian bạn An đi quãng đường AC là \({t_2} = \frac{{0,459}}{{19}}\) (giờ)
\( \Rightarrow \)Bạn An đi từ nhà đến trường hết \(t = {t_1} + {t_2} = \frac{{0,036}}{4} + \frac{{0,459}}{{19}} \approx 0,1\) giờ = 6 phút
Vậy bạn An đến trường lúc 6 giờ 6 phút.