Giải bài 19 trang 48 SBT toán 10 - Cánh diều
Trong một công trình, người ta xây dựng một cổng ra vào hình parabol (minh họa ở Hình 13) sao cho khoảng cách giữa hai chân cổng BC là 9 m
Đề bài
Trong một công trình, người ta xây dựng một cổng ra vào hình parabol (minh họa ở Hình 13) sao cho khoảng cách giữa hai chân cổng BC là 9 m. Từ một điểm M trên thân cổng người ta đo được khoảng cách tới mặt đất là MK = 1,6 m và khoảng cách từ K tới chân cổng gần nhất là BK = 0,5 m. Tính chiều cao của cổng theo đơn vị mét (làm tròn kết quả đến hàng phần mười)
Phương pháp giải - Xem chi tiết
Gắn hệ trục tọa độ cho cổng parabol, lập phương trình parabol thể hiện cổng
Lời giải chi tiết
Đặt hệ trục tọa độ như hình vẽ:
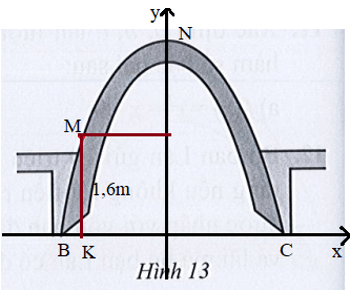
Tọa độ các điểm lần lượt là: B(– 4,5; 0); C(4,5; 0);
Vì BK = 0,5 m nên OK = 4,5 – 0,5 = 4 m. Do đó M(4; 1,6).
Cổng có hình parabol nên gọi phương trình hàm số là \(y = a{x^2} + bx + c\) (a ≠ 0) (1).
Điểm B thuộc parabol nên thay tọa độ điểm B vào (1) ta được:
\(a{( - 4,5)^2} + b( - 4,5) + c = 0 \Leftrightarrow 20,25a - 4,5b + c = 0\) (2).
Điểm C thuộc parabol nên thay tọa độ điểm C vào (1) ta được:
\(a{( 4,5)^2} + b( 4,5) + c = 0 \Leftrightarrow 20,25a + 4,5b + c = 0\) (3).
Điểm M thuộc parabol nên thay tọa độ điểm M vào (1) ta được:
\(1,6 = a{.4^2} + b.4 + c \Leftrightarrow 16a + 4b + c = 0\) (4).
Từ (2), (3) và (4) ta có hệ:
\(\left\{ {\begin{array}{*{20}{c}}{20,25 - 4,5b + c = 0}\\{20,25 + 4,5b + c = 0}\\{16a + 4b + c = 1,6}\end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{a = - \frac{{32}}{{85}}}\\{b = 0}\\{c = \frac{{648}}{{85}}}\end{array}} \right.} \right.\)
Suy ra parabol cần tìm là \(y = \frac{{ - 32}}{{85}}{x^2} + \frac{{288}}{{85}}x\).
Điểm N là điểm đỉnh của parabol thuộc vào trục tung Oy nên hoành độ điểm N bằng 0.
Thay x = 0 vào hàm số ta được \(y = \frac{{648}}{{85}}\), đó cũng chính là chiều cao của cổng.
Vậy chiều cao của cổng khoảng 7,6 m.