Giải Bài 2.30 trang 37 sách bài tập Toán 6 Kết nối tri thức với cuộc sống
Cho 6 hình vuông đơn vị, ta có hai cách xếp chúng để tạo thành các hình chữ nhật như hình dưới đây: a) Nếu cho 7 hình vuông đơn vị thì ta có mấy cách xếp chúng thành các hình chữ nhật? b) Nếu cho 12 hình vuông đơn vị thì ta có mấy cách xếp chúng thành các hình chữ nhật? c) Cho n hình vuông đơn vị (n > 1). Với những số n nào thì ta chỉ có một cách xếp chúng thành hình chữ nhật? Với những số n nào thì ta có nhiều hơn một cách xếp chúng thành hình chữ nhật?
Đề bài
Cho 6 hình vuông đơn vị, ta có hai cách xếp chúng để tạo thành các hình chữ nhật như hình dưới đây:
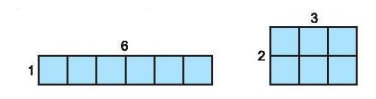
a) Nếu cho 7 hình vuông đơn vị thì ta có mấy cách xếp chúng thành các hình chữ nhật?
b) Nếu cho 12 hình vuông đơn vị thì ta có mấy cách xếp chúng thành các hình chữ nhật?
c) Cho n hình vuông đơn vị (n > 1). Với những số n nào thì ta chỉ có một cách xếp chúng thành hình chữ nhật? Với những số n nào thì ta có nhiều hơn một cách xếp chúng thành hình chữ nhật?
Phương pháp giải - Xem chi tiết
+Số hình vuông đơn vị bằng diện tích của hình chữ nhật xếp được. Do đó, ta cần tìm các bộ gồm 2 số có tích là số hình vuông
+Có bao nhiêu bộ số thì có bấy nhiêu cách xếp hình chữ nhật
Lời giải chi tiết
a) Ta có 7 = 7. 1
Do vậy ta có 1 cách xếp chúng thành hình chữ nhật.
Vậy ta xếp 1 hàng 7 hình vuông đơn vị
b) Ta có 12 = 12. 1 = 6. 2 = 4. 3
Do vậy ta có 3 cách xếp chúng thành hình chữ nhật.: Xếp 1 hàng 12 hình vuông đơn vị; 2 hàng mỗi hàng có 6 hình vuông đơn vị hoặc 3 hàng có 4 hình vuông đơn vị.
c) +Nếu n là số nguyên tố, ta chỉ có một cách xếp chúng thành hình chữ nhật vì n = n. 1
Khi đó ta xếp 1 hàng n hình vuông đơn vị.
+ Nếu n là hợp số thì n có nhiều hơn 1 cách phân tích thành tích của các số nên có nhiều hơn 1 cách sắp xếp chúng thành hình chữ nhật.
Vậy khi n là số nguyên tố, ta chỉ có một cách xếp chúng thành hình chữ nhật. Khi n là hợp số thì n có nhiều hơn 1 cách sắp xếp chúng thành hình chữ nhật.