Giải bài 2 trang 45 sách bài tập toán 8 - Chân trời sáng tạo tập 2
Cho tam giác nhọn ABC, kẻ trung tuyến AM \(\left( {M \in BC} \right)\). Gọi I là trung điểm của AM, đường thẳng CI cắt AB tại E. Từ M kẻ đường thẳng song song với CE cắt AB tại F. Chứng minh:
Đề bài
Cho tam giác nhọn ABC, kẻ trung tuyến AM \(\left( {M \in BC} \right)\). Gọi I là trung điểm của AM, đường thẳng CI cắt AB tại E. Từ M kẻ đường thẳng song song với CE cắt AB tại F. Chứng minh:
a) \(EF = FB\);
b) \(AE = \frac{1}{3}AB\);
c) \(CE = 4EI\).
Phương pháp giải - Xem chi tiết
+ Sử dụng kiến thức về đường trung bình của tam giác để chứng minh: Đường thẳng đi qua trung điểm một cạnh của tam giác và song song với cạnh thứ hai thì đi qua trung điểm cạnh thứ ba.
+ Sử dụng kiến thức về tính chất của đường trung bình của tam giác để chứng minh: Đường trung bình của tam giác thì song song với cạnh thứ ba và bằng nửa cạnh ấy.
Lời giải chi tiết
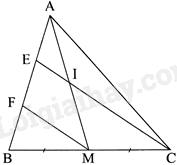
a) Tam giác BCE có: \(MB = MC\), MF//CE nên \(EF = FB\)
b) Tam giác AFM có: \(AI = IM\), EI//FM nên \(AE = EF\)
Do đó, \(AE = EF = FB\). Vậy \(AE = \frac{1}{3}AB\)
c) Tam giác BCE có: \(MB = MC\), \(EF = FB\) nên MF là đường trung bình của tam giác. Do đó, \(CE = 2MF\).
Tam giác AFM có: \(AI = IM\), \(AE = EF\) nên IE là đường trung bình của tam giác AMF. Do đó, \(MF = 2EI.\)
Vậy \(CE = 4EI\)