Giải bài 2 trang 78 SGK Toán 7 tập 2 - Chân trời sáng tạo — Không quảng cáo

Đề bài

Cho tam giác ABC vuông tại A. Trên tia BA lấy điểm M sao cho BM = BC. Tia phân giác của góc B cắt AC tại H. Chứng minh rằng MH vuông góc với BC.

Lời giải chi tiết

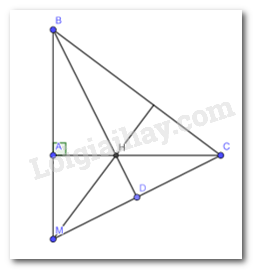
Gọi D giao điểm của tia phân giác của góc B và MC

Xét tam giác BDM và tam giác BDC có :

BD chung

$\widehat {MBD} = \widehat {CBD}$ ( BD là phân giác của góc B)

BM = BC ( giả thiết )

$\Rightarrow \Delta BDM=\Delta BDC$(c.g.c)

$\Rightarrow \widehat {BDM} = \widehat {BDC}$(2 góc tương ứng)

Mà 2 góc ở vị trí kề bù $\Rightarrow \widehat {BDM} = \widehat {BDC} = {90^o} \Rightarrow BD \bot CM$

Mà AC cắt BD tại H $\Rightarrow$ H là trực tâm tam giác BMC

$\Rightarrow$ MH là đường cao của tam giác BMC (định lí 3 đường cao đi qua trực tâm tam giác)

$\Rightarrow$ MH vuông góc với BC