Giải bài 3.30 trang 80 SGK Toán 8 - Cùng khám phá
Hàng rào được đóng từ các thanh gỗ thẳng như trong Hình 3.75 với các thanh
Đề bài
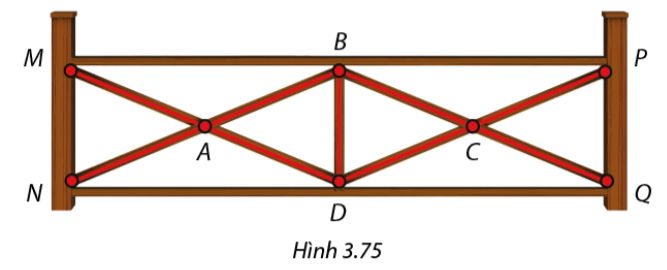
Hàng rào được đóng từ các thanh gỗ thẳng như trong Hình 3.75 với các thanh \(BN,BQ,DM,DP\) đều bằng 1,3 cm và thanh \(BD\) dài 0,5 cm. Điểm A là trung điểm chung của hai thành \(BN\)và \(DM\), điểm \(C\) là trung điểm chung của hai thanh \(BQ\) và \(DP\).
a) Chứng minh rằng tứ giác \(ABCD\) là hình thoi.
b) Tính khoảng cách giữa hai điểm A và C.
Phương pháp giải - Xem chi tiết
Dựa vào tính chất hai tam giác bằng nhau để chứng minh \(ABCD\) là hình thoi.
Sau đó tính khoảng cách giữa hai điểm A và C.
Lời giải chi tiết
a) Ta có:
Điểm A là trung điểm chung của hai thành \(BN\)và \(DM\)
Mà \(BN = DM\)
→ \(AB = AD\)
Điểm \(C\) là trung điểm chung của hai thanh \(BQ\) và \(DP\)
Mà \(BQ = DP\)
→ \(BC = CD\)
Mà \(BN = BQ = MD = DP\)
→ \(AB = AD = CB = CD\)
→ Tứ giác \(ABCD\) là hình thoi
b) Xét hình thoi \(ABCD\), ta có:
\(AB = AD = CB = CD = \frac{{1,3}}{2} = 0,65m\)
\(BD = 0,5m\)
\(AC = \sqrt {0,{{65}^2} - {{\left( {\frac{{0,5}}{2}} \right)}^2}} .2 = 1,2m\)
Vậy khoảng cách từ \(A\) đến \(C\) là \(1,2m\)