Giải bài 3 trang 128 sách bài tập toán 11 - Chân trời sáng tạo tập 1 — Không quảng cáo

Đề bài

Cho hình hộp ABCD.A’B’C’D’. Chứng minh:

a) (BDA’)//(B’D’C).

b) Đường chéo AC’ đi qua trọng tâm G và G’ của hai tam giác BDA’ và B’D’C.

c) G và G’ chia AC’ thành ba phần bằng nhau.

Lời giải chi tiết

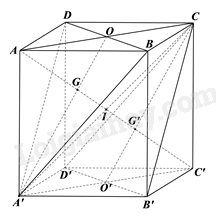
a) Ta có: DD’//BB’ và \(DD' = BB'\) (do ABCD.A’B’C’D’ là hình hộp), suy ra DD’B’B là hình bình hành, suy ra BD//B’D’, mà \(B'D' \subset \left( {B'D'C} \right)\), BD không nằm trong mặt phẳng (B’D’C) nên BD//(B’D’C).

Chứng minh tương tự ta có: DA’//(B’D’C)

Mà BD và DA’ cắt nhau tại D và nằm trong mặt phẳng (BDA’) nên (BDA’)//(B’D’C).

b) Gọi O, O’ lần lượt là tâm của hai đáy ABCD và A’B’C’D’.

Trong hình bình hành AA’C’C gọi I là giao điểm của AC’ và A’C, AC’ cắt A’O tại \({G_1}\)

Trong tam giác AA’C, ta có \({G_1}\) là giao điểm của hai trung tuyến AI và A’O nên \({G_1}\) là trọng tâm của tam giác AA’C. Suy ra \(A'{G_1} = \frac{2}{3}A'O\)

Mà G là trọng tâm của tam giác A’BD nên \(A'G = \frac{2}{3}A'O\)

Do đó, \(G \equiv {G_1}\) hay G là giao điểm của AC’ và A’O.

Chứng minh tương tự ta có trọng tâm G’ của tam giác B’D’C là giao điểm của AC’ và CO’.

Vậy AC’ đi qua trọng tâm của hai tam giác BDA’ và B’D’C.

c) Ta có: \(AG = \frac{2}{3}AI = \frac{2}{3}.\frac{1}{2}AC' = \frac{1}{3}AC',C'G' = \frac{2}{3}C'I = \frac{2}{3}.\frac{1}{2}AC' = \frac{1}{3}AC'\)

Do đó \(GG' = AC' - AG - C'G' = AC' - \frac{1}{3}AC' - \frac{1}{3}AC' = \frac{1}{3}AC'\)

Do đó, \(AG = GG' = G'C'\). Vậy G và G’ chia AC’ thành ba phần bằng nhau.