Giải Bài 34 trang 115 sách bài tập toán 7 tập 1 - Cánh diều — Không quảng cáo

Đề bài

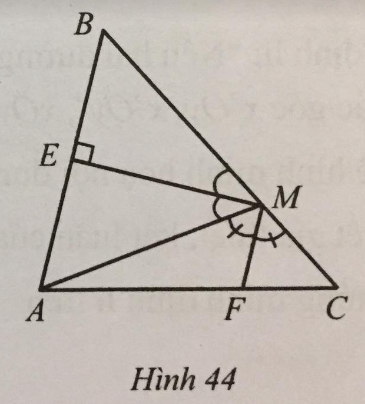
Quan sát Hình 44 , biết ME vuông góc với AB tại E và ME, MF lần lượt là tia phân giác của góc AMB và AMC . Vì sao hai đường thẳng MF và AB song song với nhau?

Lời giải chi tiết

Do hai góc AME và AMF là hai góc kề nhau nên $\widehat {EMF} = \widehat {AME} + \widehat {AMF}$.

Ta có ME, MF lần lượt là tia phân giác của góc AMB và AMC nên

$\widehat {AME} = \dfrac{1}{2}\widehat {AMB};{\rm{ }}\widehat {AMF} = \dfrac{1}{2}\widehat {AMC}$.

Mà $\widehat {AMB} + \widehat {AMC} = 180^\circ$ (hai góc kề bù) nên

$\widehat {EMF} = \widehat {AME} + \widehat {AMF} = \dfrac{1}{2}\left( {\widehat {AMB} + \widehat {AMC}} \right) = \dfrac{1}{2}{\rm{ }}{\rm{. 180}}^\circ {\rm{  =  90}}^\circ$.

Suy ra: $\widehat {EMF} = \widehat {MEB}$ mà hai góc này ở vị trí so le trong nên MF // AB (Dấu hiệu nhận biết 2 đường thẳng song song)