Giải bài 4.16 trang 55 sách bài tập toán 8 - Kết nối tri thức với cuộc sống
Cho tam giác ABC, các đường trung tuyến BD, CE. Gọi M, N theo thứ tự là trung điểm của BE, CD.
Đề bài
Cho tam giác ABC, các đường trung tuyến BD, CE. Gọi M, N theo thứ tự là trung điểm của BE, CD. Gọi I, K theo thứ tự là giao điểm của MN với BD và CE. Chứng minh \(MI = IK = KN\).
Phương pháp giải - Xem chi tiết
+ Sử dụng kiến thức về đường trung bình của tam giác để chứng minh: Đường trung bình của tam giác song song với cạnh thứ ba và bằng nửa cạnh ấy.
+ Sử dụng kiến thức về định lí Thalès đảo để chứng minh: Nếu một đường thẳng cắt hai cạnh của một tam giác và định ra trên hai cạnh này những đoạn thẳng tương ứng tỉ lệ thì đường thẳng đó song song với cạnh còn lại của tam giác.
Lời giải chi tiết
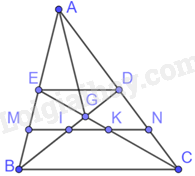
Vì CE là trung tuyến của tam giác ABC nên \(AE = EB\)
Vì M là trung điểm của BE nên \(EM = \frac{1}{2}EB\)
Do đó, \(\frac{{EM}}{{AE}} = \frac{1}{2}\) (1)
Vì BD là trung tuyến của tam giác ABC nên \(AD = DC\)
Vì N là trung điểm của DC nên \(DN = \frac{1}{2}CD\)
Do đó, \(\frac{{DN}}{{AD}} = \frac{1}{2}\) (2)
Từ (1) và (2) ta có: \(\frac{{EM}}{{AE}} = \frac{{DN}}{{AD}}\)
Tam giác AMN có: \(\frac{{EM}}{{AE}} = \frac{{DN}}{{AD}}\) nên ED//MN
Tam giác EBD có: MI//ED (cmt), M là trung điểm của BE nên I là trung điểm BD. Do đó, \(\frac{{MI}}{{ED}} = \frac{1}{2}\) (1)
Tam giác ECD có: NK//ED (cmt), N là trung điểm của DC nên K là trung điểm EC. Do đó, \(\frac{{KN}}{{ED}} = \frac{1}{2}\) (2)
Tam giác ABC có E, D lần lượt là trung điểm của AB, AC nên ED là đường trung bình của tam giác ABC. Do đó, \(\frac{{ED}}{{BC}} = \frac{1}{2}\) (3) và ED//BC
Từ (1), (2), (3) có: \(\frac{{MI}}{{BC}} = \frac{{KN}}{{BC}} = \frac{1}{4}\) (4)
Tam giác EBC có: KM//BC (cùng song song với ED), M là trung điểm của BE nên K là trung điểm của EC.
Do đó, MK là đường trung bình của tam giác EBC.
Suy ra: \(\frac{{MK}}{{BC}} = \frac{1}{2}\), hay \(\frac{{MI + IK}}{{BC}} = \frac{1}{2}\), mà \(\frac{{MI}}{{BC}} = \frac{1}{4}\) nên \(\frac{{IK}}{{BC}} = \frac{1}{4}\) (5)
Từ (4) và (5) ta có: \(MI = IK = KN\)