Giải bài 4. 29 trang 65 sách bài tập toán 10 - Kết nối tri thức với cuộc sống — Không quảng cáo

Đề bài

Cho tam giác đều $ABC$ có độ dài cạnh bằng 1.

a)      Gọi $M$ là trung điểm của $BC.$ Tính tích vô hướng của các cặp vectơ $\overrightarrow {MA}$ và $\overrightarrow {BA} ,$ $\overrightarrow {MA}$ và $\overrightarrow {AC} .$

b)     Gọi $N$ là điểm đối xứng với $B$ qua $C.$ Tính tích vô hướng $\overrightarrow {AM} .\overrightarrow {AN}$

c)      Lấy điểm $P$ thuộc đoạn $AN$ sao cho $AP = 3PN.$ Hãy biểu thị các vectơ $\overrightarrow {AP} ,\,\,\overrightarrow {MP}$ thuộc hai vectơ $\overrightarrow {AB}$ và $\overrightarrow {AC} .$ Tính độ dài đoạn $MP.$

Lời giải chi tiết

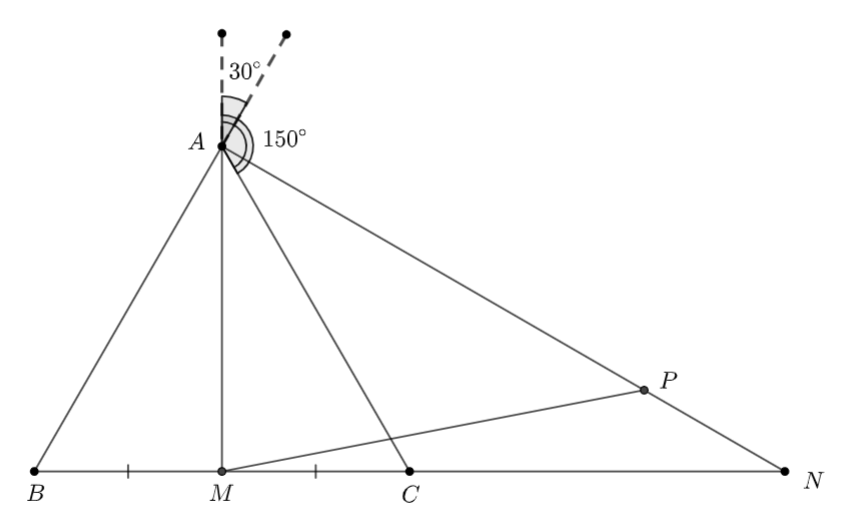
a) Xét $\Delta ABC$ đều cạnh bằng 1 có: $M$ là trung điểm của cạnh $BC$

$\Rightarrow \,\,\left\{ {\begin{array}{*{20}{c}}{AM = \frac{{\sqrt 3 }}{2}}\\{\left( {\overrightarrow {MA} ,\overrightarrow {BA} } \right) = {{30}^ \circ }}\\{\left( {\overrightarrow {MA} ,\overrightarrow {AC} } \right) = {{150}^ \circ }}\end{array}} \right.$

Ta có: $\overrightarrow {MA} .\overrightarrow {BA}  = \left| {\overrightarrow {MA} } \right|.\left| {\overrightarrow {BA} } \right|.\cos \left( {\overrightarrow {MA} ,\overrightarrow {BA} } \right) = \frac{{\sqrt 3 }}{2}.\cos {30^ \circ } = \frac{{\sqrt 3 }}{2}.\frac{{\sqrt 3 }}{2} = \frac{3}{4}$

$\overrightarrow {MA} .\overrightarrow {AC}  = \left| {\overrightarrow {MA} } \right|.\left| {\overrightarrow {AC} } \right|.\cos \left( {\overrightarrow {MA} ,\overrightarrow {AC} } \right) = \frac{{\sqrt 3 }}{2}.\cos {150^ \circ } = \frac{{\sqrt 3 }}{2}.\left( { - \frac{{\sqrt 3 }}{2}} \right) = \frac{{ - 3}}{4}$

b) Ta có: $MN = CM + CN = \frac{1}{2} + 1 = \frac{3}{2}$

Ta có: $\widehat {MAN} = {60^ \circ }$

Xét $\Delta AMN$ vuông tại $M$ có:

$AN = \sqrt {A{M^2} + M{N^2}}  = \sqrt {{{\left( {\frac{{\sqrt 3 }}{2}} \right)}^2} + {{\left( {\frac{3}{2}} \right)}^2}}  = \sqrt 3$

Ta có: $\overrightarrow {AM} .\overrightarrow {AN}  = \left| {\overrightarrow {AM} } \right|.\left| {\overrightarrow {AN} } \right|.\cos \left( {\overrightarrow {AM} ,\overrightarrow {AN} } \right) = \frac{{\sqrt 3 }}{2}.\sqrt 3 .\cos {60^ \circ } = \frac{3}{2}.\frac{1}{2} = \frac{3}{4}$

c) Ta có: $P$ thuộc đoạn $AN$ sao cho $AP = 3PN.$

Nên $\overrightarrow {AP}  = \frac{3}{4}\overrightarrow {AN}  = \frac{3}{4}\left( {\overrightarrow {AC}  + \overrightarrow {CN} } \right) = \frac{3}{4}\left( {\overrightarrow {AC}  + \overrightarrow {BC} } \right) = \frac{3}{4}\left( {2\overrightarrow {AC}  - \overrightarrow {AB} } \right)$

Ta có: $\overrightarrow {MP}  = \overrightarrow {AP}  - \overrightarrow {AM}  = \frac{3}{4}\left( {2\overrightarrow {AC}  - \overrightarrow {AB} } \right) - \frac{1}{2}\left( {\overrightarrow {AB}  + \overrightarrow {AC} } \right) = \overrightarrow {AC}  - \frac{5}{4}\overrightarrow {AB}$

Ta có: $AP = \frac{3}{4}AN = \frac{{3\sqrt 3 }}{4}$

$\Rightarrow$ $MP = \sqrt {A{P^2} + A{M^2} - 2AP.AM.\cos \widehat {MAP}}  = \frac{{\sqrt {21} }}{4}$