Giải bài 4.59 trang 73 sách bài tập toán 11 - Kết nối tri thức với cuộc sống
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Mặt phẳng (P) chứa đường thẳng AD và cắt hai cạnh SB, SC lần lượt tại E, F.
Đề bài
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Mặt phẳng (P) chứa đường thẳng AD và cắt hai cạnh SB, SC lần lượt tại E, F.
a) Xác định giao tuyến của hai mặt phẳng (EAB) và (FCD).
b) Chứng minh rằng tứ giác AEFD là hình thang.
c) Xác định giao tuyến của hai mặt phẳng (ECD) và (FAB).
d) Chứng minh rằng giao tuyến của hai mặt phẳng (ECD) và (FAB) song song với giao tuyến của hai mặt phẳng (EAB) và (FCD).
Phương pháp giải - Xem chi tiết
+ Nếu hai mặt phẳng chứa hai đường thẳng song song với nhau thì giao tuyến của chúng (nếu có) song song với hai đường thẳng đó hoặc trùng với một trong hai đường thẳng đó.
+ Để tìm giao tuyến của hai mặt phẳng, ta đi tìm hai điểm chung thuộc cả hai mặt phẳng đó rồi nối hai điểm chung đó lại ta được giao tuyến cần tìm.
Lời giải chi tiết
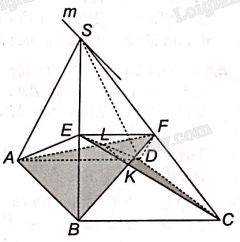
a) Vì AB//CD nên giao tuyến của hai mặt phẳng (EAB) và (FCD) là đường thẳng m đi qua S và song song với AB.
b) Vì AD//BC nên AD//(SBC)
Vì mặt phẳng (P) chứa đường thẳng AD song song với mặt phẳng (SBC) nên giao tuyến EF của hai mặt phẳng đó song song với AD. Do đó, tứ giác AEFD là hình thang.
c) Trong mặt phẳng (AEDF), gọi L là giao điểm của AF và ED.
Trong mặt phẳng (SBC), gọi K là giao điểm của BF và CE.
Khi đó, giao tuyến của hai mặt phẳng (ECD) và (FAB) là đường thẳng KL.
d) Hai mặt phẳng (ECD) và (FAB) lần lượt chứa hai đường thẳng song song là AB và CD nên giao tuyến KL của hai mặt phẳng đó song song với AB. Do đó, KL//m.