Giải bài 4 trang 65 SGK Toán 8 – Cánh diều — Không quảng cáo

Đề bài

Cho tam giác ABC nhọn có H là trực tâm. Gọi M, N, P, Q lần lượt là trung điểm của các đoạn thẳng AB, BH, HC, CA. Chứng minh tứ giác MNPQ là hình chữ nhật.

Lời giải chi tiết

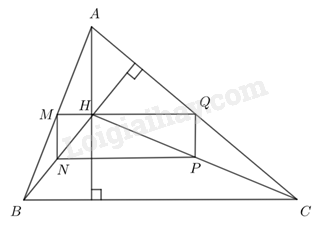
Vì M, N lần lượt là trung điểm của các đoạn thẳng AB, BH nên ta có:

MN là đường trung bình tam giác ABH $\Rightarrow MN//AH$ mà $AH \bot BC$ nên $MN \bot BC$ (1)

Vì P, Q lần lượt là trung điểm của các đoạn thẳng CH, AC nên ta có:

PQ là đường trung bình tam giác AHC $\Rightarrow PQ//AH$ mà $AH \bot BC$ nên $QP \bot BC$ (2)

Vì P, N lần lượt là trung điểm của các đoạn thẳng CH, BH nên ta có:

PN là đường trung bình tam giác BHC $\Rightarrow PN//BC$ mà $AH \bot BC$ nên $PN \bot AH$(3)

Vì M, Q lần lượt là trung điểm của các đoạn thẳng AB, AC nên ta có:

MQ là đường trung bình tam giác ABC $\Rightarrow MQ//BC$ mà $AH \bot BC$ nên $MQ \bot AH$(4)

Từ (1), (2), (3), (4) ta có $\widehat {MNP} = \widehat {NPQ} = \widehat {PQM} = \widehat {QMN} = 90^\circ$

Vậy tứ giác MNPQ là hình chữ nhật (dhnb).