Giải bài 4 trang 71 vở thực hành Toán 8
Cho ∆ABC có trọng tâm G. Vẽ đường thẳng d qua G và song song với AB,
Đề bài
Cho ∆ABC có trọng tâm G. Vẽ đường thẳng d qua G và song song với AB, d cắt BC tại điểm M. Chứng minh rằng \(BM = \frac{1}{3}BC.\)
Phương pháp giải - Xem chi tiết
Áp dụng định lí Thalès: Nếu một đường thẳng song song với một cạnh của tam giác và cắt hai cạnh cong lại thì nó định ra trên hai cạnh đó những đoạn thẳng tương ứng tỉ lệ.
Lời giải chi tiết
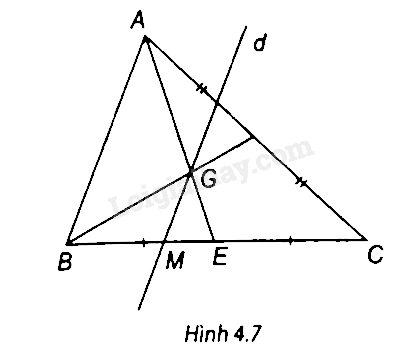
AG cắt BC tại E.
Ta có GM // AB suy ra \(\frac{{BM}}{{BE}} = \frac{{AG}}{{AE}}\) (định lí Thales).
Ta lại có \(\frac{{AG}}{{AE}} = \frac{2}{3}\) (G là trọng tâm ∆ABC) nên \(\frac{{BM}}{{BE}} = \frac{2}{3}.\)
Suy ra \(BM = \frac{2}{3}BE = \frac{2}{3}.\frac{1}{2}BC = \frac{1}{3}BC.\)
AG cắt BC tại E.
Ta có GM // AB suy ra \(\frac{{BM}}{{BE}} = \frac{{AG}}{{AE}}\) (định lí Thales) .
Ta lại có \(\frac{{AG}}{{AE}} = \frac{2}{3}\) (G là trọng tâm ∆ABC) nên \(\frac{{BM}}{{BE}} = \frac{2}{3}.\)
Suy ra \(BM = \frac{2}{3}BE = \frac{2}{3}.\frac{1}{2}BC = \frac{1}{3}BC.\)