Giải bài 4 trang 64 vở thực hành Toán 8
Cho hình vuông ABCD. Lấy một điểm E trên cạnh CD. Tia phân giác của góc DAE cắt cạnh DC tại M.
Đề bài
Cho hình vuông ABCD. Lấy một điểm E trên cạnh CD. Tia phân giác của góc DAE cắt cạnh DC tại M. Đường thẳng qua M vuông góc với AE cắt BC tại N. Chứng minh DM + BN = MN.
Phương pháp giải - Xem chi tiết
Chứng minh MD = MH, BN = HN ⇒ DM + BN = MH + HN = MN.
Lời giải chi tiết
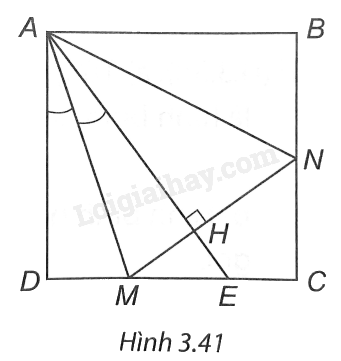
(H.3.41). Gọi H là giao điểm của AE với MN. Xét hai tam giác vuông ADM và AHM có: AM là cạnh chung, \(\widehat {DAM} = \widehat {HAM}.\) ⇒ ∆ADM = ∆AHM (cạnh huyền – góc nhọn) ⇒ MD = MH và AD = AH. Xét hai tam giác vuông AHN và ABN có: AN là cạnh chung, AH = AB (vì cùng bằng AD). ⇒ ∆AHN = ∆ABN (cạnh huyền – cạnh góc vuông) ⇒ HN = BN. Vậy DM + BN = MH + HN = MN.
Cùng chủ đề:
Giải bài 4 trang 64 vở thực hành Toán 8