Giải bài 4 trang 58 vở thực hành Toán 8
Xét một điểm M trên cạnh huyền của tam giác ABC vuông cân tại A. Gọi N và P lần lượt là hình chiếu vuông góc của M trên các cạnh AB và AC.
Đề bài
Xét một điểm M trên cạnh huyền của tam giác ABC vuông cân tại A. Gọi N và P lần lượt là hình chiếu vuông góc của M trên các cạnh AB và AC.
a) Hỏi tứ giác MPAN là hình gì?
b) Hỏi M ở vị trí nào thì đoạn thẳng NP có độ dài ngắn nhất? Vì sao?
Phương pháp giải - Xem chi tiết
a) Chứng minh tứ giác MPAN có 3 góc vuông nên là hình chữ nhật.
b) Dựa vào tính chất đường trung tuyến của tam giác vuông.
Lời giải chi tiết
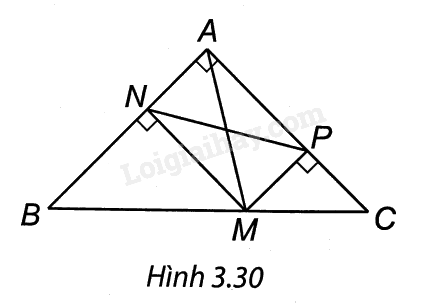
(H.3.30). a) Tứ giác MPAN có góc vuông tại A, P, N nên là một hình chữ nhật.
b) Vì MPAN là hình chữ nhật nên NP = AM.
Với điểm M tùy ý trên BC, H là chân đường cao hạ từ A của tam giác ABC, khi đó ta có AM ≥ AH.
Vậy AM nhỏ nhất khi AM = AH, tức khi M trùng H (với H là trung điểm của BC do tam giác ABC vuông cân tại A).
Do đó NP ngắn nhất khi M là trung điểm của BC.