Giải bài 4 trang 53 vở thực hành Toán 8
Cho hình bình hành ABCD. Gọi E, F lần lượt là trung điểm của các cạnh AB, CD. Chứng minh rằng:
Đề bài
Cho hình bình hành ABCD. Gọi E, F lần lượt là trung điểm của các cạnh AB, CD. Chứng minh rằng:
a) Hai tứ giác AEFD, AECF là những hình bình hành.
b) EF = AD, AF = EC.
Phương pháp giải - Xem chi tiết
a) Sử dụng dấu hiệu nhận biết để chứng minh hai tứ giác là hình bình hành.
b) Dựa vào các hình bình hành ta có các cặp cạnh tương ứng bằng nhau.
Lời giải chi tiết
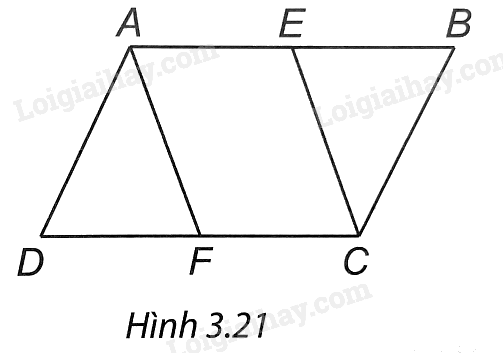
(H.3.21). a) Do ABCD là hình bình hành nên AB // CD, AB = CD, từ đó AE // CF, AE = EB = DF = FC.
Do đó tứ giác AEFD là hình bình hành.
Tương tự, tứ giác AECF là hình bình hành vì có hai cạnh đối AE và CF song song và bằng nhau.
b) Vì AEFD là hình bình hành nên AD = EF.
Vì AECF là hình bình hành nên AF = EC.
Cùng chủ đề:
Giải bài 4 trang 53 vở thực hành Toán 8