Giải bài 4 trang 45 vở thực hành Toán 8
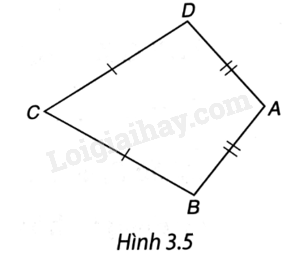
Tứ giác ABCD trong Hình 3.5 có AB = AD, CB = CD được gọi là hình “cái diều”.
Đề bài
Tứ giác ABCD trong Hình 3.5 có AB = AD, CB = CD được gọi là hình “cái diều”.
a) Chứng minh rằng AC là đường trung trực của đoạn thẳng BD.
b) Tính các góc B, D biết rằng \(\widehat A = {100^0},\widehat C = {60^0}{\rm{.}}\)
Phương pháp giải - Xem chi tiết
a) Chứng minh A và C cách đều B và D => AC là đường trung trực của BD.
b) Cách 1. Nối A và C. Tính góc B, D dựa vào đường phân giác AC của các góc BCD và BAD.
Cách 2. Nối B và D. Tính góc B, D dựa vào tính chất của tam giác cân.
Lời giải chi tiết
a) Ta có AB = AD, CB = CD nên A, C cách đều B và D, do đó AC là đường trung trực của BD.
b) Cách 1. Nối A và C. Ta có AC là trung trực của BD nên AC là đường phân giác của các góc BCD và BAD.
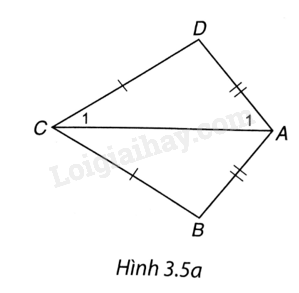
Trong \(\Delta ADC\) có
\(\begin{array}{l}\widehat D = {180^0} - \left( {\widehat {{A_1}} + \widehat {{C_1}}} \right)\\ = {180^0} - \frac{1}{2}\left( {\widehat A + \widehat C} \right)\\ = {180^0} - \frac{1}{2}\left( {{{100}^0} + {{60}^0}} \right)\\ = {100^0}\end{array}\)
Tương tự ta cũng có \(\widehat B = {100^0}\).
Cách 2. Nối B, D. Tam giác ABD cân tại đỉnh A nên \(\widehat {{D_1}} = \frac{1}{2}\left( {{{180}^0} - \widehat A} \right) = {40^0}\)
Tam giác CBD cân tại đỉnh C nên \(\widehat {{D_2}} = \frac{1}{2}\left( {{{180}^0} - \widehat C} \right) = {60^0}\).
Từ đó \(\widehat D = \widehat {{D_1}} + \widehat {{D_2}} = {40^0} + {60^0} = {100^0}\)
Tương tự ta cũng có \(\widehat B = {100^0}\).