Giải Bài 5 trang 60 sách bài tập toán 7 - Chân trời sáng tạo
Cho tam giác ABC có hai đường trung tuyến AM và BN cắt nhau tại G. Vẽ AH vuông góc với BC tại H. Cho biêý HB = HM. Chứng minh:
Đề bài
Cho tam giác ABC có hai đường trung tuyến AM và BN cắt nhau tại G. Vẽ AH vuông góc với BC tại H. Cho biêý HB = HM. Chứng minh:
a) \(\Delta ABH = \Delta AMH\)
b) \(AG = \frac{2}{3}AB\)
Phương pháp giải - Xem chi tiết
- Kiểm tra ba cạnh tương ứng của hai tam giác ABH và tam giác AMH
- Sử dụng tính chất của ba đường trung tuyến
Lời giải chi tiết
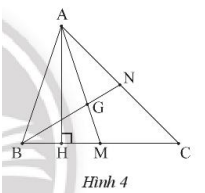
a) Ta có AH là trung trực của đoạn BM, suy ra AB = AM.
Xét hai tam giác ABH và AMH có:
Cạnh AH chung
HB = HM
AB = AM
Suy ra: \(\Delta ABH = \Delta AMH(c - c - c)\)
b) G là trọng tâm tam giác ABC.
Suy ra: \(AG = \frac{2}{3}AM\)
Theo câu a ta có: \(AB = AM\)
Suy ra: \(AG = \frac{2}{3}AB\)
Cùng chủ đề:
Giải Bài 5 trang 60 sách bài tập toán 7 - Chân trời sáng tạo