Giải bài 6 trang 99 sách bài tập Toán 6 - Chân trời sáng tạo Tập 2
Ba đường thẳng phân biệt có thể tạo ra bao nhiêu góc? Hãy vẽ hình trong các trường hợp đó.
Đề bài
Ba đường thẳng phân biệt có thể tạo ra bao nhiêu góc? Hãy vẽ hình trong các trường hợp đó.
Phương pháp giải - Xem chi tiết
Bước 1: Liệt kê các trường hợp có thể xảy ra của 3 đường thẳng
Bước 2: Mỗi trường hợp, để đếm số góc ta làm như sau: Đếm số đỉnh chung, mỗi đỉnh chung đó có bao nhiêu tia (giải sử là n) thì đỉnh chung đó tạo thành n(n-1):2 góc.
Lời giải chi tiết
Trường hợp 1: có một giao điểm:
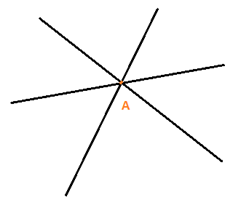
1 đỉnh chung, có 6 tia
Vậy số góc tạo thành là 6.5:2 = 15 góc
Trường hợp 2: có hai giao điểm
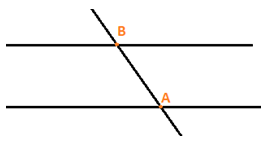
2 đỉnh chung, mỗi đỉnh có 4 tia
Vậy số góc tạo thành là 2.4.3:2 = 12 góc
Trường hợp 3: có 3 giao điểm
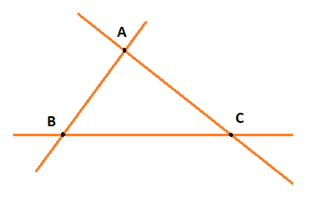
3 đỉnh chung, mỗi đỉnh có 4 tia
Vậy số góc tạo thành là 3.4.3:2 = 18 góc
Trường hợp 4: không có giao điểm nào

Vậy không có góc nào được tạo thành.