Giải bài 61. Luyện tập chung trang 35, 36, 37 vở bài tập Toán 5 - Cánh diều — Không quảng cáo

Bài 1

Trả lời Bài 1 Trang 35 VBT Toán 5 Cánh Diều

Quan sát hình vẽ:

a) Viết số đo thích hợp.

b) Tính diện tích xung quanh và diện tích toàn phần của mỗi hình.

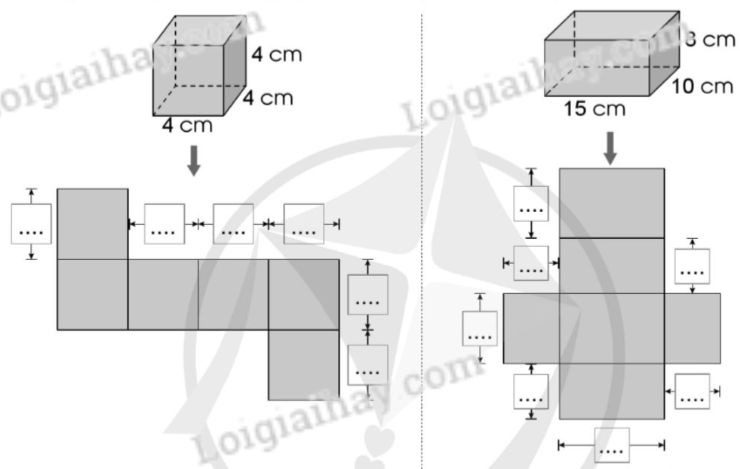
Phương pháp giải:

a) Quan sát hình và dựa vào tính chất của hình hộp chữ nhật, hình lập phương.

b)

- Muốn tính diện tích xung quanh của hình hộp chữ nhật ta lấy chu vi mặt đáy nhân với chiều cao (cùng một đơn vị đo).

- Muốn tính diện tích toàn phần của hình hộp chữ nhật ta lấy diện tích xung quanh cộng với diện tích hai đáy.

- Diện tích xung quanh của hình lập phương bằng diện tích một mặt nhân với 4.

- Diện tích toàn phần của hình lập phương bằng diện tích một mặt nhân với 6.

Lời giải chi tiết:

a,b)$400 + 15 \times 10 \times 2 = 700$

S _{xung quanh} = $4 \times 4 \times 4 = 64$ (cm ² )                                S _{xung quanh} = $\left( {10 + 15} \right) \times 2 \times 8 = 400$ (cm ² )

S _{toàn phần} = $4 \times 4 \times 6 = 96$(cm ² )                                   S _{toàn phần} = (cm ² )

Bài 2

Trả lời Bài 2 Trang 35 VBT Toán 5 Cánh Diều

Viết số thích hợp vào chỗ chấm:

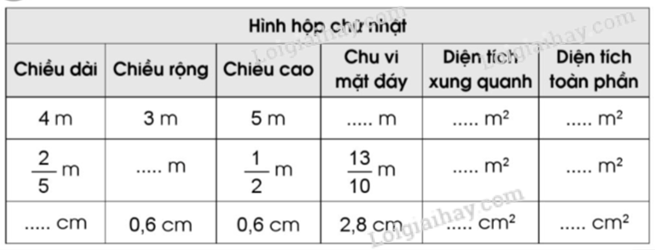
Phương pháp giải:

- Muốn tính diện tích xung quanh của hình hộp chữ nhật ta lấy chu vi mặt đáy nhân với chiều cao (cùng một đơn vị đo).

- Muốn tính diện tích toàn phần của hình hộp chữ nhật ta lấy diện tích xung quanh cộng với diện tích hai đáy.

Lời giải chi tiết:

Bài 3

Trả lời Bài 3 Trang 36 VBT Toán 5 Cánh Diều

a) Một ngăn kéo làm bằng gỗ có dạng hình hộp chữ nhật với kích thước như hình bên. Tính diện tích phần gỗ của ngăn kéo đó.

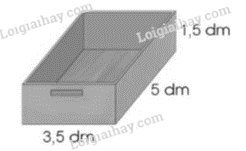
b) Một đoạn ống thép có có dạng hình hộp chữ nhật với kích thước như hình bên. Tính diện tích thép đủ để làm 30 đoạn ống như thế.

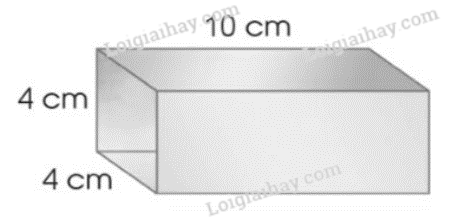
Phương pháp giải:

a) Ngăn kéo không có mặt trên nên diện tích phần gỗ của ngăn kéo là tổng của diện tích xung quanh của ngăn kéo và diện tích đáy của ngăn kéo.

b) Đoạn ống thép không có 2 đầu và rỗng ở giữa nên diện tích ống thép là diện tích xung quanh của ống thép.

- Tính diện tích thép đủ để làm 30 đoạn ống = diện tích xung quanh của ống thép x 30

Lời giải chi tiết:

a) Diện tích xung quanh của ngăn kéo là:

$\left( {3,5 + 5} \right) \times 2 \times 1,5 = 25,5$(dm ² )

Diện tích đáy của ngăn kéo là:

$3,5 \times 5 = 17,5$(dm ² )

Diện tích phần gỗ của ngăn kéo đó là:

25,5 + 17,5 = 43 (dm ² )

Đáp số: 43 dm ² .

b) Diện tích xung quanh của ống thép là:

$\left( {4 + 10} \right) \times 2 \times 4 = 112$(cm ² )

Diện tích thép đủ để làm 30 đoạn ống là:

$112 \times 30 = 3360$ (cm ² )

Đáp số: 3 360 cm ² .

Bài 4

Trả lời Bài 4 Trang 36 VBT Toán 5 Cánh Diều

Quan sát các hình sau và cho biết mảnh bìa nào có thể gấp thành hình lập phương, hình hộp chữ nhật.

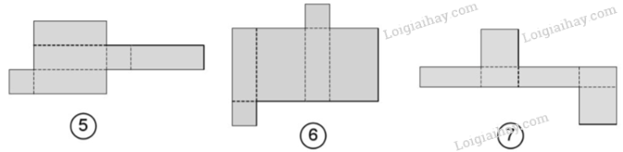
- Các mảnh bìa số .................. có thể gấp thành hình lập phương.

- Các mảnh bìa số .................. có thể gấp thành hình hộp chữ nhật.

Phương pháp giải:

Quan sát hình, dựa vào tính chất của hình lập phương và hình hộp chữ nhật để trả lời.

Lời giải chi tiết:

- Các mảnh bìa số 1 và 3 có thể gấp thành hình lập phương.

- Các mảnh bìa số 5 có thể gấp thành hình hộp chữ nhật.

Bài 5

Trả lời Bài 5 Trang 37 VBT Toán 5 Cánh Diều

Một công ty sản xuất hai loại hộp bằng bìa cứng có dạng hình hộp chữ nhật với kích thước như bảng dưới đây:

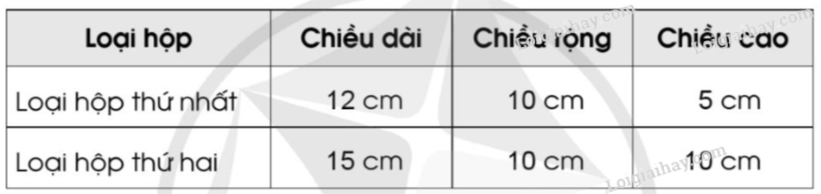
a) Tính diện tích bìa cần dùng để làm một chiếc hộp mỗi loại để hoàn thiện bảng sau:

b) Ước lượng số tiền mua bìa để sản xuất một chiếc hộp mỗi loại, biết rằng cứ 1 m ² bìa thì làm được khoảng 20 chiếc hộp loại thứ nhất và làm được khoảng 12 chiếc hộp loại thứ hai. Loại bìa được sử dụng có giá là 24000 đồng 1 m ² .

Trả lời: ................................................................................................................

Phương pháp giải:

a) Diện tích bìa cần dùng để làm một chiếc hộp mỗi loại = diện tích toàn phần của mỗi chiếc hộp

b) Tính giá tiền mua bìa để sản xuất một chiếc hộp mỗi loại = số tiền 1 m ² bìa : số hộp

Lời giải chi tiết:

a)

b) Số tiền mua bìa để sản xuất một chiếc hộp loại thứ nhất là:

24 000 : 20 = 1 200 (đồng)

Số tiền mua bìa để sản xuất một chiếc hộp loại thứ hai là:

24 000 : 12 = 2 000 (đồng)

Đáp số: Loại 1: 1200 đồng;

Loại 2: 2000 đồng.