Giải bài 7 trang 105 vở thực hành Toán 8 tập 2
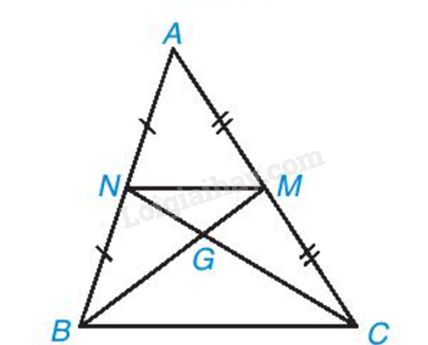
Hai đường trung tuyến BM, CN của tam giác ABC cắt nhau tại điểm G (H.9.75). Chứng minh rằng tam giác GMN đồng dạng với tam giác GBC và tìm tỉ số đồng dạng
Đề bài
Hai đường trung tuyến BM, CN của tam giác ABC cắt nhau tại điểm G (H.9.75). Chứng minh rằng tam giác GMN đồng dạng với tam giác GBC và tìm tỉ số đồng dạng
Phương pháp giải - Xem chi tiết
Chứng minh tam giác GMN và tam giác GBC có NM // BC
Lời giải chi tiết
Hai tam giác GMN và GBC có $\widehat{GMN}=\widehat{GBC},\widehat{BNM}=\widehat{GCB}$ (các cặp góc so le trong)
Do đó $\Delta GMN\backsim \Delta GBC$ (g.g) với tỉ số đồng dạng bằng $\frac{MN}{BC}=\frac{1}{2}$.
Cùng chủ đề:
Giải bài 7 trang 105 vở thực hành Toán 8 tập 2