Giải bài 7 trang 61 sách bài tập toán 12 - Cánh diều
Trong mỗi ý a), b), c), d), chọn phương án đúng (Đ) hoặc sai (S). Cho hình chóp (S.ABC) có (SA = SB = SC = AB = AC = a) và (BC = asqrt 2 ) (Hình 9). a) Tam giác (ABC) vuông tại (A) và tam giác (SAB) đều. b) (overrightarrow {AB} .overrightarrow {AC} = 0) và (left( {overrightarrow {SA} ,overrightarrow {AB} } right) = {120^ circ }). c) (overrightarrow {SC} .overrightarrow {AB} = frac{{{a^2}}}{2}). d) (cos left( {overrightarrow {SC} ,overrightarrow {AB} } r
Đề bài
Trong mỗi ý a), b), c), d), chọn phương án đúng (Đ) hoặc sai (S).
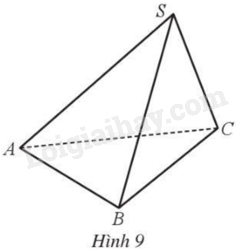
Cho hình chóp \(S.ABC\) có \(SA = SB = SC = AB = AC = a\) và \(BC = a\sqrt 2 \) (Hình 9) .
a) Tam giác \(ABC\) vuông tại \(A\) và tam giác \(SAB\) đều.
b) \(\overrightarrow {AB} .\overrightarrow {AC} = 0\) và \(\left( {\overrightarrow {SA} ,\overrightarrow {AB} } \right) = {120^ \circ }\).
c) \(\overrightarrow {SC} .\overrightarrow {AB} = \frac{{{a^2}}}{2}\).
d) \(\cos \left( {\overrightarrow {SC} ,\overrightarrow {AB} } \right) = \frac{1}{2}\).
Phương pháp giải - Xem chi tiết
‒ Sử dụng tích vô hướng của hai vectơ: \(\overrightarrow a .\overrightarrow b = \left| {\overrightarrow a } \right|.\left| {\overrightarrow b } \right|.\cos \left( {\overrightarrow a ,\overrightarrow b } \right)\).
Lời giải chi tiết
Xét tam giác \(ABC\) có: \(A{B^2} + A{C^2} = 2{a^2} = B{C^2}\). Vậy tam giác \(ABC\) vuông tại \(A\).
Xét tam giác \(SAB\) có: \(SA = SB = AB = a\). Vậy tam giác \(SAB\) đều.
Vậy a) đúng.
Tam giác \(ABC\) vuông tại \(A\) nên \(AB \bot AC \Leftrightarrow \left( {\overrightarrow {AB} ,\overrightarrow {AC} } \right) = {90^ \circ }\). Vậy \(\overrightarrow {AB} .\overrightarrow {AC} = 0\).
\(\overrightarrow {SA} .\overrightarrow {AB} = - \overrightarrow {AS} .\overrightarrow {AB} = - \left| {\overrightarrow {AS} } \right|.\left| {\overrightarrow {AB} } \right|.\cos \left( {\overrightarrow {AS} ,\overrightarrow {AB} } \right) = - a.a.\cos {60^ \circ } = - \frac{{{a^2}}}{2}\)
\(\cos \left( {\overrightarrow {SA} ,\overrightarrow {AB} } \right) = \frac{{\overrightarrow {SA} .\overrightarrow {AB} }}{{\left| {\overrightarrow {SA} } \right|.\left| {\overrightarrow {AB} } \right|}} = \frac{{ - \frac{{{a^2}}}{2}}}{{a.a}} = - \frac{1}{2} \Rightarrow \left( {\overrightarrow {SA} ,\overrightarrow {AB} } \right) = {120^ \circ }\).
Vậy b) đúng.
\(\overrightarrow {SC} .\overrightarrow {AB} = \left( {\overrightarrow {SA} + \overrightarrow {AC} } \right).\overrightarrow {AB} = \overrightarrow {SA} .\overrightarrow {AB} + \overrightarrow {AC} .\overrightarrow {AB} = - \frac{{{a^2}}}{2} + 0 = - \frac{{{a^2}}}{2}\). Vậy c) sai.
\(\cos \left( {\overrightarrow {SC} ,\overrightarrow {AB} } \right) = \frac{{\overrightarrow {SC} .\overrightarrow {AB} }}{{\left| {\overrightarrow {SC} } \right|.\left| {\overrightarrow {AB} } \right|}} = \frac{{ - \frac{{{a^2}}}{2}}}{{a.a}} = - \frac{1}{2}\). Vậy d) sai.
a) Đ
b) Đ
c) S
d) S