Giải bài 7 trang 67 Chuyên đề học tập Toán 10 – Cánh diều
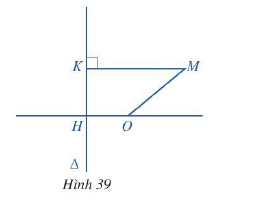
Cho đường thẳng \(\Delta \) và điểm O sao cho khoảng cách từ O đến \(\Delta \) là OH = 1 (Hình 39). Với mỗi điểm M di động trong mặt phẳng, gọi K là hình chiếu vuông góc của M lên \(\Delta \). Chứng minh tập hợp các điểm M trong mặt phẳng sao cho \(M{K^2} - M{O^2} = 1\) là một đường parabol.
Đề bài
Cho đường thẳng \(\Delta \) và điểm O sao cho khoảng cách từ O đến \(\Delta \) là OH = 1 (Hình 39). Với mỗi điểm M di động trong mặt phẳng, gọi K là hình chiếu vuông góc của M lên \(\Delta \). Chứng minh tập hợp các điểm M trong mặt phẳng sao cho \(M{K^2} - M{O^2} = 1\) là một đường parabol.
Lời giải chi tiết
Chọn hệ trục toạ độ sao cho điểm O trùng với gốc toạ độ và trục Ox trùng với đường thẳng OH.
Giả sử M có toạ độ (x; y) thì K có toạ độ là (–1; y).
Khi đó:
\(\begin{array}{l}M{K^2} - M{O^2} = 1\\ \Rightarrow {\left( {x + 1} \right)^2} + {\left( {y - y} \right)^2} - {\left( {0 - x} \right)^2} - {\left( {0 - y} \right)^2} = 1\\ \Rightarrow {x^2} + 2x + 1 - {x^2} - {y^2} = 1 \Rightarrow {y^2} = 2x\end{array}\)
Vậy tập hợp các điểm M là parabol có phương trình \({y^2} = 2x\)