Giải Bài 7 trang 87 sách bài tập toán 7 tập 1 - Chân trời sáng tạo
Phát biểu giả thiết, kết luận, vẽ hình minh họa và chứng minh định lí: “Nếu một tứ giác có ba góc vuông thì góc còn lại cũng là góc vuông”.
Đề bài
Phát biểu giả thiết, kết luận, vẽ hình minh họa và chứng minh định lí: “Nếu một tứ giác có ba góc vuông thì góc còn lại cũng là góc vuông”.
Lời giải chi tiết
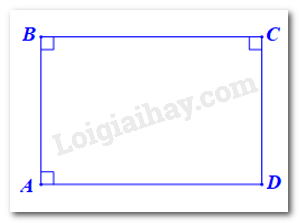
Viết giả thiết và kết luận bằng kí hiệu:
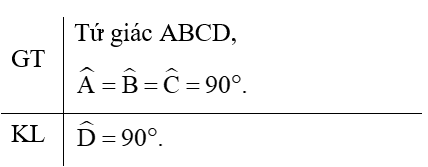
Chứng minh định lí:
Vì \(\widehat A\)=\(\widehat B\)=90° nên AB ⊥ BC, AB ⊥ AD.
Do đó BC // AD (hai đường thẳng cùng vuông góc với một đường thẳng thứ ba thì song song)
Mà \(\widehat C\)=90° nên BC ⊥ CD.
Ta có BC // AD và BC ⊥ CD.
Do đó AD ⊥ CD (một đường thẳng vuông góc với một trong hai đường thẳng song song thì nó cũng vuông góc với đường thẳng còn lại).
Suy ra \(\widehat D\)=90°.
Vậy \(\widehat D\)=90°.
Cùng chủ đề:
Giải Bài 7 trang 87 sách bài tập toán 7 tập 1 - Chân trời sáng tạo