Giải bài 8 trang 62 vở thực hành Toán 8 tập 2
Cho hàm số bậc nhất y = (m + 2)x + 3 a) Tìm m để đồ thị hàm số song song với đường thẳng y = −x
Đề bài
Cho hàm số bậc nhất y = (m + 2)x + 3
a) Tìm m để đồ thị hàm số song song với đường thẳng y = −x
b) Vẽ đồ thị hàm số với giá trị m tìm được ở câu a
c) Tìm giao điểm A của đồ thị hàm số tìm được ở câu a và đồ thị của hàm số y = x + 1. Tính diện tích của tam giác OAB, trong đó B là giao điểm của đồ thị hàm số y = x + 1 với trục Ox
Phương pháp giải - Xem chi tiết
a) Dựa vào hai đường thẳng song song để tìm giá trị của m.
b, Xác định hai điểm thuộc mỗi đồ thị rồi vẽ đồ thị hàm số.
c) Xác định tọa độ các điểm A, B. Tính AB, OA, OB.
Gọi H là chân đường vuông góc hạ tử A xuống trục hoành.
Tính diện tích tam giác OAB = \(\frac{1}{2}\) AH.OB.
Lời giải chi tiết
a) Đồ thị hàm số song song với đường thẳng y = –x khi m + 2 = −1, tức là m = –3.
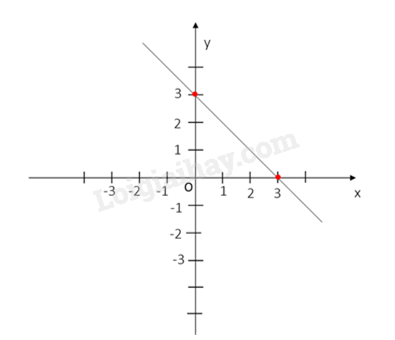
b) Với m = –3, ta có hàm số y = −x + 3. Đồ thị của hàm số này như hình bên.
c)
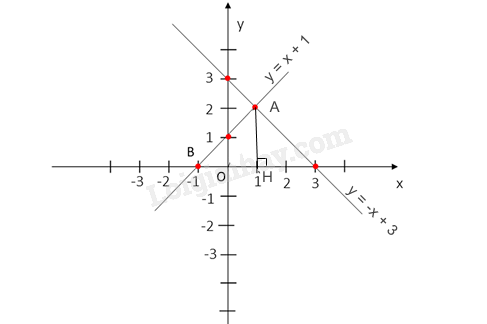
Giao điểm của đồ thị hàm số tìm được ở câu a với đồ thị của hàm số y = x + 1 là A(1; 2).
Giao điểm của đồ thị hàm số y = x + 1 với trục hoành là B(-1; 0).
Do đó OB = 1.
Gọi H là chân đường vuông góc hạ từ A xuống trục hoành. Ta có: H(1, 0) và AH = |y A | = 2.
Diện tích tam giác OAB là S OAB = \(\frac{1}{2}\)AH.OB = \(\frac{1}{2}\).2.1 = 1 (đơn vị diện tích).